В машиностроительном производстве, как и во всех других областях производственной деятельности человека, практически всегда возникают задачи выбора наиболее эффективного варианта решения из множества технически допустимых. При проектировании технологического процесса изготовления изделия эти задачи приобретают конкретные формы, связанные с выбором методов обработки, состава и последовательности технологических операций, технологического оснащения и режимов резания.

Дорогой технологический процесс (операция, переход) должный быть эффективным, т.е. наилучшим c позиций выбранного критерия оптимальности К_о. При этом должны быть удовлетворены разного рода ограничения, которые формируют область допустимых решений. Для конкретного варианта технологического процесса механической обработки такой тезис означает необходимость расчета оптимальных режимов резания, то есть поиск оптимальных значений искомых параметров Х технологического процесса.

Кроме искомых параметров, технологический процесс характеризуется совокупностью фазовых и исходных параметров Y, являющихся функциями искомых независимых параметров (например, сила и мощность резания, стойкость инструмента и др.). Кроме того, в математическую модель процесса входят постоянные для решаемой задачи параметры V: коэффициенты уравнений и другие. Все ограничения представляются в виде системы неравенств, каждое из которых дает допустимые границы варьирования соответствующего фазового или искомого параметра (например, наибольшее допустимое значение силы резания, частоты вращения шпинделя и т.п.). Аналитически это можно записать в виде:

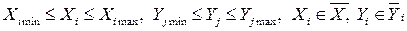.        (1.1)

Критерий оптимальности - функция исходных и искомых параметров:

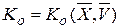.                                          (1.2)

Предполагается, что этот критерий необходимо или максимизировать (K_о ® мах), или минимизировать (K_о ® min). Поиск вектора искомых параметров, который доставляет максимальное (минимальное) значение критерия K_о, осуществляется на некотором множестве G допустимых решений:

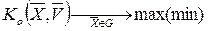.                                                            (1.3)

Таким образом, задача поиска оптимальных режимов резания описывается следующей математической моделью:

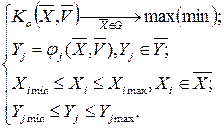                                (1.4)

Полученная модель позволяет классифицировать исходную задачу оптимизации как задачу математического программирования, которая в зависимости от вида ограничений и целевой функции относится к одному из следующих классов задач: линейного, нелинейного, дискретного, динамического и стохастического программирования.