Рассмотренные ранее метод сил и метод перемещений могут быть использованы при расчете самых произвольных статически неопределимых систем. Однако каждый из них имеет свою рациональную область применения. Например, для рам с прямолинейными стержнями, имеющими в основном жесткие узлы, рациональнее применять метод перемещений. В шарнирно-стержневых системах, в системах со стержнями ломаного очертания, неизвестных метода сил обычно меньше, чем метода перемещений.
 |  |
М.п. h=2 М.п. h=3
М.с. h=6 М.п. h=1
Встречаются системы, в которых можно выделить одну часть более удобную для расчета методом перемещений, а другая более удобна для расчета методом сил.
P
 | |||
 | |||
2 эт. q h1
| | |||
 | |||
1 эт. h2
 |  |  |  |  |
l1 l2 l3
| Этаж | Степень статической неопределимости | Степень кинематической неопределимости |
| 1 этаж 2 этаж | 9 2 | 2 4 |
| Итого | 11 | 6 |
Как видно из таблицы, здесь первый этаж более рационально решать методом перемещений, а второй – методом сил.
Метод, в котором принимают часть неизвестных метода сил, а часть – метода перемещений, называется смешанным. Предложен метод Ф. Блейхом (конец XIX в) и развит в канонической форме А.А. Гвоздевым (1927 год).
X1 X2 P
 |  |
X2 X1
q
Z3 Z4
 |  |
Условиями эквивалентности заданной и основной систем в этом случае будут равенство нулю перемещений по направлению неизвестных X1 и X2 и равенство нулю реактивных усилий в связях 3 и 4.
В канонической форме эти условия запишутся:
; (1)
Уравнения (1) – канонические уравнения смешанного метода.
Коэффициенты dik определяют как в методе сил, путем перемножения эпюр с помощью интеграла Мора:
;
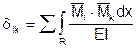для вычисления, которого можно использовать правило Верещагина или формулу Симпсона, dik = dki.
Коэффициенты rik- определяют как в обычном методе перемещений. Это реактивное усилие в связи i от единичного смещения связи k. rik = rki
Между коэффициентами со штрихами существует связь:
И проще определить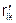 
который представляет собой реактивное усилие в связи i от действия силы Xk = 1 , а затем приравнять 
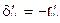. Либо 
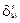определяют из эпюры перемещений.
Смешанный метод обладает преимуществом над другими в тех случаях, когда одна часть рамы обладает повышенной подвижностью, а другая – повышенной жесткостью.
Пример: P = 6 кН 2EI
 | |||
 | |||
EI
4м q = 2 кН / м
 | |||
 | |||
4м EI 2EI
| | |  |
6м
Комбинированное решение задачи
Комбинированное решение может быть использовано при расчете только симметричных статически неопределимых рам.
Сущность комбинированного приема расчета рассмотрим на примере:
с
а) б)
EIP
P P/2 P/2 P/2 P/2
h EIC EIC
 |  |
l
Преобразуем нагрузку в прямосимметричную и обратносимметричную группы так, чтобы сумма этих двух загружений а) и б) давала нам исходное.
Для каждого из этих загружений легко установить число неизвестных при расчете рамы методом сил и методом перемещений.
а) При симметричном загружении:
Z1 Z2 = - Z1 X1
Z3 = 0 X2 X2
 | |||||
 |  | ||||
P/2 P/2 P/2 P/2
| |  |  |  | ||||||||
 |  | ||||||||||
о.с. м.п. о.с. м.с.
 |  | | |
Z2 = - Z1 ; Z3 = 0 X3 = 0
одно неизвестное два неизвестных.
Вывод: симметричную раму на действие прямосимметричной нагрузки проще решать методом перемещений.
б) При обратно симметричном загружении:
Z1 Z2 = Z1 X1
 | | ||||
| | |||||
Z3
P/2 P/2 P/2 X1 P/2
| |  | | | ||||||||
 |  | ||||||||||
о.с. м.п. о.с. м.с.
 | |||||
| |  | ||||
Z1 = Z2 X2 = 0 ; X3 = 0
два неизвестных одно неизвестное.
Вывод: симметричную раму на действие кососимметричной нагрузки проще решать методом сил.
Порядок расчета симметричных рам комбинированным способом:
1. Произвольно действующую нагрузку преобразуют в прямо- и обратносимметричное загружение.
2. Независимо рассчитывают две рамы: а) на прямосимметричное загружение методом перемещений; б) на обратносимметричное загружение – методом сил.
3. Сумма двух полученных результирующих эпюр и даст нам эпюру M для заданного загружения:
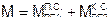
Учебное издание
КОНСПЕКТ ЛЕКЦИЙ по дисциплине
«СТРОИТЕЛЬНАЯ МЕХАНИКА»
(для студентов строительных специальностей)
Часть 2
Мущанов Владимир Филиппович
Жук Николай Романович
Гижко Виктор Терентьевич
Дата: 2019-02-19, просмотров: 218.
