Основная трудность применения метода сил при расчете рам, имеющих большую степень статической неопределимости, связана с определением коэффициентов и решением системы канонических уравнений. При расчете симметричных рам, имеется ряд приемов, позволяющих часть побочных коэффициентов dik(i ¹ k) обратить в нуль.
Одним из таких приемов является использование симметрии рамы при выборе основной системы метода сил. Т.е. основную систему необходимо выбрать симметричной, причем постараться, чтобы как можно большее число неизвестных было в виде прямо- и обратносимметричных усилий.
Прямосимметричные неизвестные создают симметричные эпюры моментов, а обратносимметричные неизвестные — кососимметричные эпюры. Результат перемножения таких эпюр:
 = 0 .
= 0 .
 |
 Ì X1
Ì X1

 X3 X3
X3 X3













 X2
X2

 I2
I2
X1

 h I1 I1 q
h I1 I1 q
 |  | |||
 |  | |||







 h = 3 О.С.
h = 3 О.С.
 |  |
l

Единичные и грузовая эпюры имеют вид :
 l/2 X1=1 l/2 1 1
l/2 X1=1 l/2 1 1


 X2=1
X2=1
 |  | ||||||||||||||
 | |||||||||||||||
 |  | ||||||||||||||
 |  |  | |||||||||||||







 X1=1 X3=1 X3=1
X1=1 X3=1 X3=1
 |  |  |  |  |  | ||||||||
 |  |  |  |  |  | ||||||||
 |  |  |  |  |  | ||||||||
 |  |  |  |  |  | ||||||||






 qh2/2
qh2/2
 |  |  |  |  |  |  | |||||||||||||||
 |  |  |  |  |  |  | |||||||||||||||
 |  |  |  | ||||||||||||||||||

















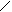
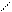


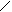
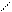












 ` M1 `M2 M3 Mp
` M1 `M2 M3 Mp
h h
Рис. 1
Тогда в нашем случае d12 = d21 = 0 ; d13 = d31 = 0 , и система из трех уравнений с тремя неизвестными :
ì d11Х1 + d12Х2 + d13Х3 + D1Р =0
í d21Х1 + d22Х2 + d23Х3 + D2Р =0
î d31Х1 + d32Х2 + d33Х3 + D3Р =0 ,
после подстановки коэффициентов превращается в одно независимое уравнение :
d11Х1 + D1Р =0 ;
и систему из двух уравнений с двумя неизвестными :
ì d22Х2 + d23Х3 + D2Р =0
î d32Х2 + d33Х3 + D3Р =0 .
Группировка неизвестных
 Часто, при расчете симметричных рам, не удается выбрать основную систему так, чтобы все неизвестные разместились на оси симметрии. Поэтому для получения симметричных и обратно симметричных эпюр приходится в качестве неизвестных применять не отдельные силы, а группы прямо- и кососимметричных сил.
Часто, при расчете симметричных рам, не удается выбрать основную систему так, чтобы все неизвестные разместились на оси симметрии. Поэтому для получения симметричных и обратно симметричных эпюр приходится в качестве неизвестных применять не отдельные силы, а группы прямо- и кососимметричных сил.
 |  |


 Ì P Ì P
Ì P Ì P
 | |||
 | |||

 I2 I2 y1 y2
I2 I2 y1 y2








 h I1
h I1








 l l h = 2
l l h = 2









 P 2l X2=1
P 2l X2=1





























 X1 X1 X1=1 X1=1 X2=1 l
X1 X1 X1=1 X1=1 X2=1 l


 l
l



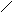

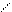
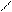
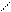

 X2 X2 `M1 `M2
X2 X2 `M1 `M2
Рис. 2
У1 = Х1 + Х2
У2 = Х1 - Х2 , d12 + d21 = 0.
таким образом система уравнений:
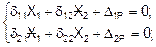 (2)
(2)
преобразуется:
d11 X1+ D1P = 0;
и
d22 X2+ D2P = 0
Преобразование нагрузки
Любую нагрузку, приложенную к симметричной раме, можно разложить на составляющие симметричного и кососимметричного вида.

 q q/2 q/2
q q/2 q/2



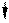
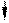

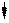
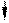

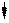
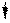
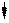
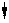
 Х2 =0 X2
Х2 =0 X2
 | |||||
 |  |








 X1 =0 X1
X1 =0 X1
 |  |  |
P P/2 P/2











 h = 4 I
h = 4 I

 q/2 X4 X3
q/2 X4 X3 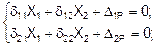




 q/2
q/2


 X3 P/2 X4 P/2
X3 P/2 X4 P/2 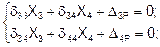
II






 Сумма двух загружений I + II
Сумма двух загружений I + II
дает исходное загружение
При загружении рамы симметричной нагрузкой в симметричных связях будут возникать только симметричные неизвестные усилия, а при загружении обратно симметричной нагрузкой — обратно симметричные усилия (см. рисунок).
Порядок расчета следующий:
1) преобразуют нагрузку в прямо симметричную и обратно симметричную;
2) рассчитывают раму независимо на прямо- и кососимметричное загружение, учитывая при этом, что при прямо симметричном загружении возникают только симметричные усилия в отброшенных связях, а при обратно симметричном загружении — только кососимметричные усилия. Это значительно сократит расчет в каждом варианте загружения. Решения доводят до построения эпюр MП.С. и MК.С ;
3) окончательную эпюру получают суммированием эпюр, полученных в каждом расчете
M = MП.С. + MК.С. .
Применение жестких консолей
Пусть требуется рассчитать три раза статически неопределимую раму
 а) б) X2 в)
а) б) X2 в)

 X1 X3
X1 X3












 P P P
P P P
 X2 d
X2 d

 I1 I1 h X1 X3 X1
I1 I1 h X1 X3 X1
X2 X2
 |  |  |  |  |  | ||||||
l h = 3
 |
Если основную систему метода сил выбрать как показано на рис б, то:
d12 = d21 = 0; d23 = d32 = 0.
Вводя в основную систему рис.в жесткие консоли (т.е. EI = ¥ ), можно добиться чтобы все побочные коэффициенты были равны нулю.
D l/2 l/2 1 1
 |  | ||||||||||
 |  | ||||||||||
 | |||||||||||
 | |||||||||||


























 X3=1
X3=1
 |  | ||||||||||
 | |||||||||||
 |  |  | |||||||||

 X1=1 X1=1
X1=1 X1=1

 X2=1
X2=1
 | ||||||||||||||||||||
 | ||||||||||||||||||||
 | ||||||||||||||||||||
 |  | |||||||||||||||||||
 |  | |||||||||||||||||||
 |  | |||||||||||||||||||
 | ||||||||||||||||||||
 |  |  |  | |||||||||||||||||
h-d  h-d
h-d 
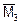
При построении эпюр, на жестких консолях эпюры не строятся, т.к. при перемножении их по правилу Верещагина, результат перемножения в пределах жестких консолей необходимо будет разделен на EI = ¥, т.е. 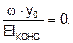
d12 = d21 = 0; d23 = d32 = 0
Чтобы и d13 = d31 = 0 подберем длину жесткой консоли из условия:
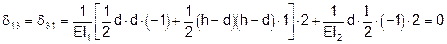
Тогда система канонических уравнений примет вид:
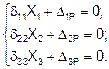
Метод упругого центра
Этот метод применяют в основном при расчете статически неопределимых арок и рам, элементы которых имеют переменные жесткости по длине.
Суть этого способа заключается в том, что с помощью специального приема добиваются, чтобы все побочные коэффициенты системы канонических уравнений были равны нулю.
Рассмотрим симметричную 3 раза статически неопределимую раму.
 |
 - IP x X1 X3 X1
- IP x X1 X3 X1
 | |||||||
 | |||||||
 | |||||||
 | |||||||
X2 X2
 h IC + IC
h IC + IC
 | |||||
 |  | ||||
l y
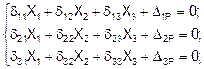
 |
x X1 = 1 X2 = 1 X3 = 1
 | |||||||||||
 |  | ||||||||||
 | |||||||||||
 | |||||||||||
 | |||||||||||




 y x
y x
 | |||||
 | |||||
 | |||||
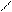
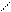
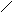

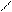
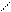
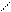
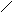

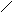


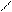
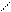
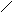
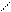
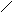






 y
y
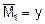
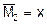
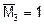
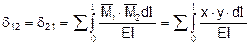
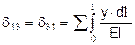 ;
; 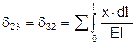
Построим упругий контур

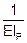
 |





 d l
d l


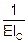
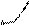








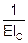
И коэффициенты запишутся:
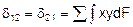 - центробежный момент инерции упругого контура относительно осей x и y
- центробежный момент инерции упругого контура относительно осей x и y
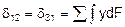 - статический момент площади упругого контура относительно оси x
- статический момент площади упругого контура относительно оси x
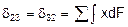 - статический момент площади упругого контура относительно оси y.
- статический момент площади упругого контура относительно оси y.
Статические моменты и центробежный момент инерции равны нулю относительно главных осей, расположенных в центре тяжести сечения.
Следовательно, если неизвестные X1 ,X2 ,X3 приложены в центре тяжести упругого контура, то все побочные коэффициенты системы канонических уравнений будут равны нулю и система запишется:
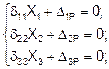
Чтобы приложить неизвестные в центре тяжести упругого контура, используются жесткие консоли.
В рассмотренном примере:




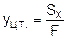




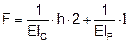 X1 X3 X1
X1 X3 X1
X2 X2

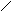


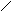


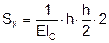
Порядок определения положения центра тяжести упругого контура следующий:
1. на заданной раме строим упругий контур, ширина которого равна 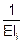 ;
;
2. выбираем систему координат, приняв в качестве одной из осей ось симметрии рамы;
3. находим положение упругого центра:
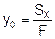
Порядок расчета рам методом сил
1. Определяют степень статической неопределимости системы:
h = CОП + 2Ш0 - 3D;
или
h = 3K- Ш0 ;
2. Выбирают наиболее рациональную основную систему метода сил (с учетом возможных упрощений).
3. Записывают систему канонических уравнений метода сил.
4. Для основной системы строят единичные `Mi и грузовую MP эпюры моментов.
5. Определяют коэффициенты системы канонических уравнений.
6. Проверяют правильность вычисления коэффициентов (универсальная, построчная и проверка грузовых коэффициентов).
7. Решают систему канонических уравнений и определяют значение неизвестных X1 ,X2 ,....,Xn . Правильность решения системы следует проверить подстановкой найденных неизвестных в систему уравнений.
8. Строят исправленные эпюры `MiXi
9. Суммируя исправленные эпюры и грузовую, получают результирующую эпюру 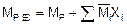
10. Проверяют правильность построения эпюры MРЕЗ:
а) должно выполнятся равенство моментов в узлах;
в) деформационная проверка ( 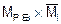 ) = 0.
) = 0.
11. По эпюре MРЕЗ строят эпюру поперечных сил Q и затем по эпюре Q - эпюру продольных сил N.
12. Выполняется статическая проверка равновесия рамы в целом :
åMK = 0;
åx = 0;
åy = 0;
в эти уравнения входит заданная нагрузка и опорные реакции, которые берут из эпюр MРЕЗ , Q, N.
13. В случае необходимости определяют перемещения указанных сечений рамы.
Определение перемещений статически неопределимых систем
Для определения перемещений статически неопределимых систем необходимо вначале построить эпюры M от действия внешней нагрузки и от действия единичной обобщенной силы, приложенной по направлению искомого перемещения. И затем перемножая эпюры по правилу Верещагина, определяют искомое перемещение. При этом грузовую эпюру строят для заданной статически неопределимой системы (решая ее любым из известных методов: метод сил, перемещений и т.д.), а единичную эпюру строят для основной системы метода сил, что значительно упрощает процесс определения необходимых перемещений. Допустимость таких упрощений докажем на примере:
а) б) DCГОР=? в)
 q q
q q




 C B HB
C B HB
 |  | ||||
 | |||||








 I1 VB
I1 VB
 | ||
 | ||

 h I2
h I2
 |

 MРЕЗ
MРЕЗ
 |  |  | |||||
 | |||||||
A l

Для заданной рамы эпюра MРЕЗ показана на рис. б. Если в опоре В отбросить две опорные связи и по направлению отброшенных связей приложить опорные реакции VB и HВ (см. рис. в), то эпюры моментов и деформации систем, показанных на рис. а и в будут одинаковы, а, следовательно, для определения Dсгор единичную эпюру можно строить как для заданной (рис. а) так и для основной (рис. в) системы метода сил, т.е.:













 P=1
P=1 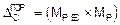

MP
 h
h
Дата: 2019-02-19, просмотров: 366.