В рамах с параллельными стойками, независимо от того горизонтальный ригель или наклонный, линейные смещения узлов равны между собой.
 D
D

 2 2'
2 2'



 D
D
 1 1'
1 1'
1-2 = 1'-2'
1-1' ½½ 2-2'
1-2-2'-1' — параллелограмм
1-1' = 2-2'
А В
 |  | ||
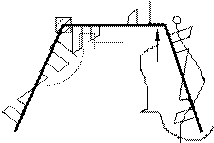
Более сложно определить зависимость между линейными смещениями узлов рам с непараллельными стойками.
 DВ2
DВ2

 DА1
DА1



 2 2'
2 2'

 1 D12
1 D12
1'
 А В
А В
 |  |
Определяют зависимость между линейными смещениями узлов с помощью диаграммы Виллио:
- выбираем точку О – полюс диаграммы, из полюса откладываем независимое смещение DВ2 по направлению перпендикулярно стойке В2 и прямые перпендикулярно А1 и перпендикулярно ригелю 1-2
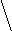
 DВ-2 2
DВ-2 2
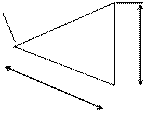 |
 О D12
О D12
 |
DА-1 1
- измеряя полученные отрезки, находим отношения
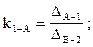
 .
.
И затем строим эпюры. От поворота моментной связи, никаких особенностей в построении эпюр нет




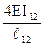





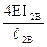




 А от линейного смещения учитывают изменение величин узловых моментов коэффициентами k12 и k1A:
А от линейного смещения учитывают изменение величин узловых моментов коэффициентами k12 и k1A:
 D2В=1 r33
D2В=1 r33





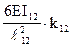

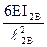




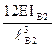


Весь остальной расчет, как в обычном методе перемещений.
Лекция №26. Использование симметрии при расчете рам методом перемещений
При расчете симметричных систем методом перемещений, так же как и при расчете методом сил, можно применять группировку неизвестных.
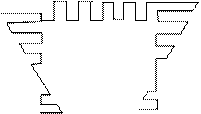
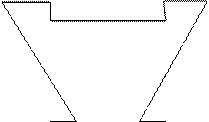
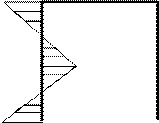
В этом случае все эпюры от единичных неизвестных будут симметричными или обратносимметричными. Ряд побочных коэффициентов обращается в нуль. Расчет значительно упрощается:

 Z2 Z2
Z2 Z2
 Z1 Z1
Z1 Z1






 Z3
Z3
EIP
 P P
P P

 EIC EIC
EIC EIC

 |


 О.С.
О.С.


 l
l


 ;
;
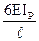
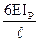
 |  | ||||||
 | |||||||
 | |||||||


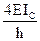
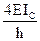
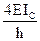

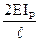

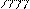
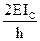
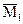
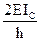
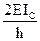
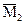
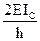





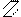

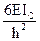
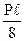
 | |||
 |
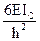 P
P 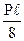
 |




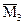
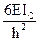
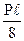
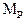
При определении коэффициентов системы канонических уравнений необходимо помнить, что реакции, как и перемещения, являются групповыми и представляют собой алгебраическую сумму реакций в связях данной группы. Например, для определения реакции r r11 необходимо на первой эпюре вырезать две связи и тогда 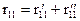
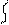


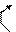
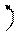 r’11 r’’11
r’11 r’’11



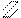


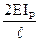
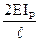


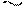

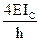
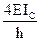


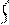


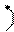 r’12 r’’12
r’12 r’’12


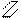
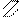







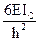
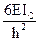 r12=0
r12=0
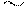


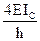
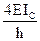
т.е. симметричная групповая реакция от кососимметричного группового перемещения равна нулю 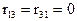 .
.
Система из трех уравнений распадается на одно уравнение и систему из двух уравнений с двумя неизвестными.
При частных видах нагрузки расчет еще более упрощается. Так, при действии на симметричную раму симметричной нагрузки в задаче останутся только симметричные неизвестные перемещения, кососимметричные будут равны нулю. При действии кососимметричной нагрузки остаются неизвестными только кососимметричные перемещения.
Например, на раму действует симметричная равномерно-распределенная нагрузка
 q q
q q






 Z1 Z1
Z1 Z1


 EIP
EIP
h EIC EIC
 | |||||||
 | |||||||
 | |||||||
 | |||||||
 . i
. i
В общем случае число неизвестных метода перемещений h=3, но учитывая что Z2=Z3=0, остается одно неизвестное
r11Z1 + R1p=0.
Дата: 2019-02-19, просмотров: 388.