Для построения линии влияния усилий в неразрезных балках, используют метод моментных фокусов.
Внутренние усилия в каком-либо сечении балки выражают через изгибающие моменты на левой и правой опорах, и усилия в этом сечении основной системы от подвижной нагрузки М0,Q0,R0.
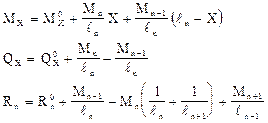
Таким образом, для построения линий влияния какого-либо усилия в неразрезной балке необходимо предварительно построить линии влияния опорных моментов.
Для этого, последовательно располагая единичный груз в каждом пролете балки, используя метод моментных фокусов, записывают аналитические зависимости рассматриваемых опорных моментов от положения единичного груза в пролете. По этим зависимостям строят линии влияния опорных моментов.
Например:
P=1
0 1 2 3
l1 l2 l3
+ л.вл. М1
- -
1. Груз Р=1 в пролете 1 .
l0=0
2. Груз Р=1 в пролете 2.
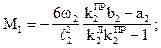
3. Груз Р=1 в пролете 3.
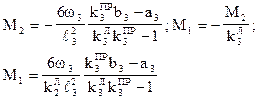
Процесс этот арифметически очень трудоемкий и, в случае необходимости, линии влияния строят, используя справочную литературу, или стандартные программы для ЭВМ.
Бывают случаи, когда необходимо представить вид линии влияния того или иного усилия в неразрезной балке. Здесь удобно построить не саму линию влияния, а ее модель, пользуясь кинематическим методом
0 1 I 2 II 3
I II
l1 l2 l3 lk
1
| | |  | | |
+ + л .вл . R1
R1 -
 |  | |
j=1
+ + л .вл . MI
- -
| | | |
D=1
- -
л.вл. QI
+ +
Порядок построения:
1. В неразрезной балке устраняется та связь, которая воспринимает рассматриваемое усилие.
2. По направлению отброшенной связи, балке задается единичное обобщенное перемещение.
3. От этого перемещения строится деформированная упругая ось балки, которая и будет представлять собой модель линии влияния интересующего нас усилия.
Лекция №31. Статически неопределимые фермы
Статически неопределимой называется геометрически неизменяемая ферма, которая имеет лишние связи.
В зависимости от того, какие связи являются лишними, различают три типа ферм:
1) фермы статически неопределимые по отношению к опорным связям;
2) фермы статически неопределимые по отношению к основным стержням;
3) фермы статически неопределимые по отношению к опорным связям и к основным стержням.
Расчет ферм ведут в основном методом сил. Степень статической неопределимости ферм может определятся по общей формуле:
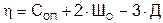, (1)
но более рационально использовать формулу:
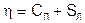(2)
где CЛ- число лишних опорных стержней фермы;
SЛ- число лишних основных стержней,
которые в свою очередь можно найти:
CЛ = СОП - 3 , (3)
SЛ = SФ - SО = SФ - 2 Y + 3, (4)
где
SO = 2Y - 3
SФ- фактическое число стержней в ферме.
Основная система метода сил
Для ферм 1го типа
X1
CЛ = 5 - 3 = 2
SЛ = 13 - 2 - 8 + 3 = 0 Основную систему получают, отбрасывая лишние связи.
Для ферм 2го типа
 | |||
 | |||
X2
X1
 |  |  |  |  |  |
CЛ = 0;
SЛ = 11 - 2- 6 + 3 = 2 Основную систему получают, разрезая лишние стержни фермы.
Для ферм 3го типа
X1
X2
 | |||||||||||||
 | | |  |  |  | ||||||||
СЛ = 4 - 3 = 1;
SЛ = 14 - 2 - 8 + 3 = 1
Основную систему выбирают, отбрасывая лишние опорные, и разрезая лишние основные стержни фермы.
Канонические уравнения метода сил для дважды статически неопределимой фермы запишутся:
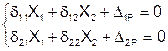
где d12 - перемещение по направлению Х1 от действия X2 = 1,
D2P - перемещение по направлению X2 от действия внешней нагрузки.
Имея ввиду, что в элементах ферм возникают только продольные усилия, коэффициенты системы канонических уравнений определяются одним слагаемым формулы Мора:
,
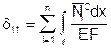
учитывая, что жесткость стержней ферм по длине постоянна (EIi = const) и постоянна продольная сила в пределах стержня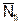 
= const:
; 
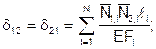
и т.д. ,
где n - число стержней в ферме.
Суммирование ведется по всем стержням фермы, в том числе и разрезанным!
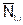- усилия во всех стержнях основной системы фермы от действия X1 = 1;
Npi- усилия во всех стержнях основной системы фермы от действия внешней нагрузки.
После того, как будут вычислены неизвестные X1, X2, Xk, усилия в стержнях заданной фермы определяются по формуле:
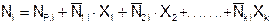
Правильность выполнения решения проверяют с помощью деформационной проверки:
Расчет ведут обычно в табличной форме:
| № стр | l, м | EF |
|
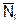
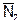
| NP |
|
|
 
|
|
|
|
|
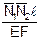
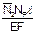
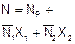
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
 1
2
:
:
n
| å = | d11 | d12=d21 | d22 | D1p | D2p | » 0 |
Дата: 2019-02-19, просмотров: 205.
