Степенью кинематической неопределимости называется число неизвестных перемещений, знание которых определяет деформированный вид системы и, следовательно, все усилия в ней. Учитывая сказанное, степень кинематической неопределимости рамы определяется:
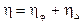(1)
здесь: hj - степень угловой подвижности рамы. Она определяется числом жестких узлов рамы, не считая опорных, т.к. их положение заранее известно. Жестким считается узел, в котором, по крайней мере, два из сходящихся стержней соединены между собой жестко.
 | |||||
 |  | ||||
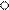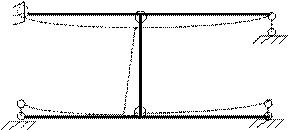
hj=4.
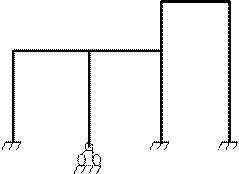
В одном узле может с помощью шарнира соединятся группа жестких узлов, например
hj=2 hj=5
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
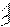шарнир
 | |||||||||
 |  | ||||||||
 |  | ||||||||
hD - степень линейной подвижности рамы, равна количеству возможных независимых линейных смещений узлов рамы.
 |
hD=1
Если визуально определить затруднительно, то заданную раму превращают в шарнирно-стержневую систему, вводя во все жесткие узлы, в том числе и опорные, шарниры. Степень свободы полученной системы и определяет степень линейной подвижности рамы.
Например:
hD=2
 | |||||||
 | |||||||
 | |||||||
 | |||||||
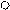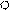Или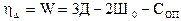 
 |
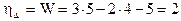
Основная система метода перемещений и канонические уравнения
После определения числа неизвестных, выбирают основную систему метода перемещений. В отличие от метода сил, где основную систему выбирают статически определимой, в методе перемещений в качестве основной системы принимается кинематически определимая система, которая образуется из заданной путем наложения на ее узлы связей, препятствующих упругим перемещениям узлов.
Вводятся связи двух типов:
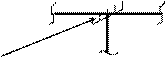
а) связи первого рода или упруго-податливые защемления, которые не дают узлам возможности поворачиваться, но не препятствуют возможным их линейным смещениям (моментные связи)
 | |||
 | |||
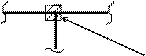Связи первого рода
Связи первого рода вводятся во все жесткие узлы рамы.
б) связи второго рода или опорные стержни, которые не мешают повороту узлов, но исключают их возможные линейные смещения
 | |||||
 | |||||
 | |||||
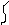связь второго рода
 |
Вводят связи второго рода по направлению возможных линейных перемещений узлов.
Рассмотрим пример выбора основной системы метода перемещений
h=1+1=2
Z1 Z2
1 2
 | |||
 | |||
Z2
 | ||||||||
 | ||||||||
 |  | |||||||
 | ||||||||
заданная система основная система
То есть основная система представляет собой набор отдельных статически неопределимых балок с постоянной жесткостью.
И дея метода: для того, чтобы основная и заданная система были равноценны в смысле деформаций и усилий, необходимо в основной системе связи повернуть на соответствующие углы и придать им линейные смещения как в заданной системе. При этом в дополнительных связях возникнут реактивные усилия. В связях первого рода – реактивные моменты, а в связях второго рода – реакции. Так как в заданной системе дополнительных связей нет, то можно записать условия равноценности: реактивные усилия в дополнительных связях от их перемещения и действия внешней нагрузки должны быть равны нулю, т.е.
,
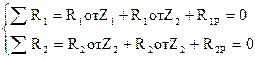обозначим
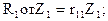
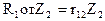; и т.д.,
где :
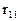– реактивное усилие в связи 1 от единичного смещения связи Z1=1, т.е. индексы при коэффициентах обозначают
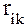
где от чего
Тогда, система канонических уравнений метода перемещений для систем с двумя неизвестными запишется
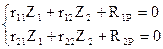
Для n-раз кинематически неопределимых систем
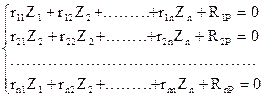(2)
Дата: 2019-02-19, просмотров: 385.
