Как указывалось выше, благодаря введению дополнительных связей, основная система метода перемещений представляет собой набор отдельных статически неопределимых балок постоянной жесткости по длине. Их опорные закрепления могут быть двух типов: жесткое защемление или шарнир (см. рис. а и б)
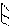
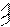
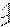
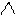


 а) б )
а) б )
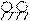 |
Поскольку мы пренебрегаем продольными деформациями элементов, то возможными перемещениями узлов балок а) и б) являются вертикальные линейные перемещения и поворот жестко закрепленного узла.
Коэффициенты, входящие в канонические уравнения, представляют собой реактивные усилия в дополнительных связях от перемещений узлов и действия внешних нагрузок. Поэтому рассмотрим напряженно-деформированное состояние отдельных балок от различных возможных видов воздействий.
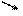
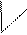 Z=1
Z=1
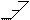

 1) EI
1) EI


 A B
A B 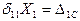
i
 X1=1
X1=1 
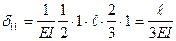
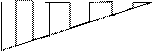


 | |||||
 | |||||
 | |||||

 1
1

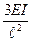
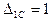
 |
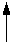
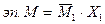

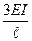
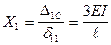
Аналогично решая задачу для других возможных видов воздействий, формируют таблицу напряженно-деформированных состояний отдельных балок.
| Эскиз балки | Эпюры и реакции | |||
                    Z=1
EI
i Z=1
EI
i
| 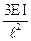
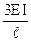
| |||
  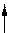 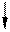          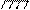         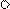 EI
Z=1
i EI
Z=1
i
|
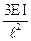 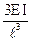
| |||
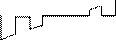           Z=1 EI
Z=1 EI
i
| 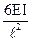 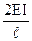
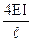
| |||
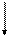                 EI
Z=1
i EI
Z=1
i
| 
 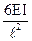
| |||
                     q q
 i i
| 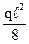
 
| |||
       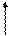 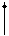     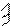  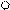   P
i/2 i/2
P
i/2 i/2
|  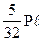
 
| |||
          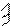      M
i
M
i
| M
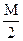

| |||
                       q
i q
i
|   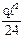 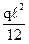
 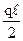
| |||
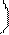          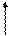 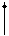   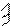 P
i/2 i/2
P
i/2 i/2
| 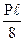 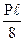 
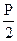 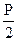
|
Порядок определения коэффициентов рассмотрим на конкретном примере:
q q
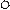





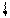 Z1 Z2
Z1 Z2





 1)
1)

 EIC EIC
EIC EIC
 О.С.
О.С.
 | |||||||
 | |||||||
 | |||||||
 | |||||||
 . l
. l
h=1+1=2.
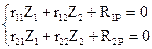
1е – уравнение называется моментным;
2е – уравнение - уравнением сдвига.
4) Для определения коэффициентов канонических уравнений необходимо построить единичные и грузовую эпюры. Эпюры строят в основной системе метода перемещений, последовательно задавая единичные смещения всем дополнительным наложенным связям и от действия внешней нагрузки, используя ранее составленную таблицу.




 Z1=1
Z1=1 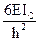 Z2=1
Z2=1














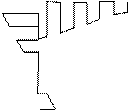
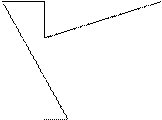


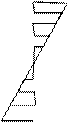



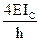
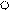 | |||
 | |||




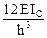
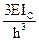




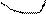


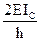
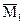
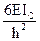




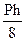
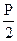
 |
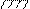
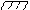

Коэффициенты моментных уравнений, представляющие собой реактивные моменты в дополнительных связях определяют путем вырезания этих дополнительных связей из соответствующих эпюр. К вырезаемой связи прикладывают реактивные моменты, взятые с эпюр и искомую реакцию связи. Искомую реакцию прикладывают так, как задавалось единичное перемещение рассматриваемой связи и затем, записывая равенство моментов в рассматриваемой связи нулю, определяют искомую реакцию.
r11 – реактивный момент в первой связи от ее единичного смещения.
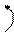
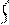 r11 åM1=0;
r11 åM1=0;


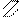




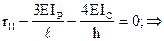
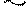

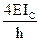
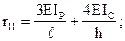
 r12
r12
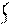 |

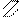

 åM1=0;
åM1=0;

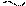
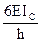
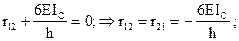
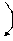
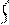
 R1P
R1P



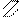

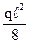 åM1=0;Þ
åM1=0;Þ 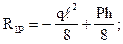
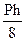

Коэффициенты уравнений сдвига, представляющие собой реактивные усилия в связях второго рода, определяют, отсекая от рамы элемент, через который передаются реакции на рассматриваемую связь, вдоль которого расположен дополнительный опорный стержень. К отсеченному элементу прикладывают искомую опорную реакцию (по направлению, как задавали единичное перемещение) и реакции стержней, которые проецируются на ось дополнительного стержня.
Из уравнения, в виде суммы проекций всех сил на направление единичного перемещения, определяем величину искомой реакции.









 r22 R2P
r22 R2P
 | |||||
 | |||||
 | |||||
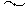
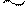

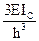
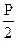
åX=0;Þ 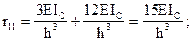 åX=0; Þ
åX=0; Þ 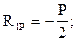
5) Проверки коэффициентов системы канонических уравнений (выполняют довольно редко):
а) универсальная: сумма всех единичных коэффициентов равна результату умножения суммарной единичной эпюры самой на себя:
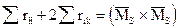
Суммарную единичную эпюру получают путем сложения всех единичных эпюр:









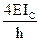 –
–
– 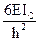


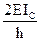 –
– 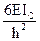
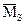
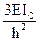
б) построчная проверка: сумма всех единичные коэффициентов i-го уравнения равна результату умножения суммарной единичной эпюры на 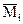 .
.
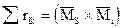
в) проверка грузовых коэффициентов: сумма всех грузовых коэффициентов равна, взятому с обратным знаком, результату умножения суммарной единичной эпюры на грузовую, построенную для основной системы метода сил:
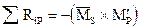 .
.
6) Коэффициенты подставляют в систему канонических уравнений и решают ее, определяя неизвестные Z1, Z2, ...... Zn .
7) После того, как найдены действительные перемещения дополнительных связей Zi, строят окончательные эпюры усилий в заданной системе.
Эпюру изгибающих моментов Mрез получают суммированием ординат грузовой эпюры MP с ординатами исправленных эпюр 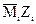 ,то есть:
,то есть:

Правильность построения окончательной эпюры изгибающих моментов проверяют теми же способами, что и в методе сил:
а) проверяется равновесие узлов рамы – в методе перемещений эта проверка является существенной, так как в основной системе равенства моментов в узле нет, а в заданной системе оно должно выполнятся;
б) выполняется деформационная проверка. Для этого выбирается основная система метода сил, строится одна из возможных единичных эпюр и :
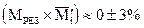
По эпюре моментов строят эпюру Q, а по эпюре Q – эпюру продольных сил N.
Дата: 2019-02-19, просмотров: 341.
