Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

       Расчет статически неопределимых систем начинают с анализа расчетной схемы сооружения. Это необходимо для того, чтобы определить степень статической неопределимости системы, которая равна числу лишних связей:

 

                              h = - W,     где         W = 3 D - 2 Ш_о - С_оп

т.е.

                                             h = С_оп + 2 Ш_о - 3 D                                      (1)

 

здесь:        C_jg - число опорных связей;

                   Ш_о - число простых шарниров;

                   D - число жестких дисков.

 

Например :

 

 

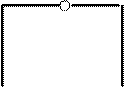
                                                                        h = 5 + 1 - 3·2 =1

   

                                

 

 

       Однако, эта формула справедлива лишь в том случае, если отдельные диски не являются замкнутыми контурами, т.е. каждый из них сам по себе статически определим. Если же рама имеет замкнутые контуры, то необходимо учитывать еще и статическую неопределимость каждого такого контура.

 

 

       P

 

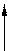
                                                                                                      M   M

                                                                               N                                N

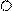
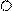                                                                                            Q        Q

                                                                                                             

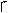
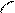
                                                                                              Замкнутый контур трижды                                                                                                                                                                    

                                                                                               статически неопределим

 

 

                                                                                         M = 0; т.е. h = 2,

                                                                              т.е. простой шарнир уменьшает

                                                                              степень стат. неопределимости                   

                                                                              замкнутого контура на 1 единицу.

 

 

       Таким образом, для рам, имеющих замкнутые контуры, степень статической неопределимости определяется по формуле:

 

                                                 h = 3 К - Ш_о                                                    (2)

 

Например:

 

                    I         II

                                                                             2                                   2

                   III      IV

 

                   h = 4·3 - 0 = 12                                        h = 3·4 - 4 = 8.

Основная система метода сил.

 

       Основная система метода сил получается из заданной путем отбрасывания “лишних” связей. Вместо отброшенных связей прикладывают неизвестные обобщенные силы X₁ , X₂ , ........, X_n.

       “Лишние” связи следует удалять таким образом, чтобы полученная основная система во всех своих частях была статически определимой и геометрически неизменяемой.

        

Способы образования основных систем:

1) можно отбросить “лишние” опорные связи, и по направлению отброшенных связей приложить неизвестные опорные реакции;

 

 

                               h = 2

 

                                                                                                                 X₂

           З.С.                                                             О.С.

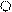                                                                                                      X₁

2) можно разрезать сплошной брус и в сечении приложить парные моменты, поперечные и продольные силы;

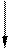
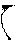
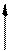                                                                                X₂ X₁      X₁     X₃

                                                                               X₃                           X₂

 

       h = 3

 

 

 

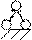
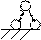
3)  можно удалить одну внутреннюю связь, вводя на ось жесткого элемента шарнир;

 

                                                                                          

                                                                                         Х₁

       h = 1

 

 

 

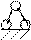4) можно сделать разрез по шарниру, это равносильно удалению двух внутренних связей: поперечной и продольной сил;

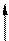                                                                               X₁                   X₁

                                                                                         X₂                          X₂

 

       h = 2

 

 

 

5) можно разрезать стержень, с двух сторон прикрепленный шарнирно к системе. В таком незагруженном стержне возникает одна продольная сила.

 

 

 

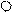
       h = 1                                                                                            X₁

 

Канонические уравнения метода сил

 

       Идея метода сил: в заданной системе перемещения по направлению отброшенных связей равны нулю. В основной системе по направлению отброшенных связей перемещения могут быть как = 0, так и ¹ 0. Чтобы заданная и основная системы были равноценны в смысле усилий и деформаций, необходимо подобрать такие усилия X₁, Х₂, . . , Х_n чтобы перемещения по направлению отброшенных связей, в основной системе, от действия внешней нагрузки и усилий X₁, Х₂, . . , Х_n также равнялись нулю.

                              P₂                                                                 P₂

       P₁                                                                       P₁

 

                              З.С.                                                     О.С.            X₁

 

                                                                                                                 X₂

       т.е.

                   D_i = D_iP + D_iX1 + D_iX2 +.......+ D_iXn  = 0

 

       где:

                   D_iXn = d_in X_n ,

       тогда

                   D_i = d_ii X_i + d_i2 X₂ + ....... + d_in X_n + D_iP = 0;

 

d_i1 - перемещение по направлению i от действия X₁ = 1.

D_iP - перемещения по направлению i от действия внешней нагрузки.

       Если система имеет n неизвестных, то система канонических уравнений метода сил запишется:

 

 

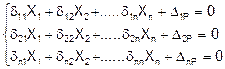
1^е уравнение: перемещение по направлению X_i от действия неизвестных X₁, X₂ , ... , X_n и внешней нагрузки, в основной системе, должно равняться нулю.

       Коэффициенты с одинаковыми индексами d_ii - называются главными коэффициентами, d_ik - побочными, причем d_ik = d_ki (на основании теоремы Максвелла), D_iP - грузовой коэффициент.