В школьном курсе математики обычно используются два основных способа решения задач: арифметический и алгебраический. Однако, кроме этих способов, рассматриваются еще и способ подбора, графический способ решения, практический способ. В принципе, все эти способы решения имеют равные права на применение их при решении задач, однако, арифметический и алгебраический являются наиболее универсальными, так как не все задачи можно корректно решить остальными способами.

Арифметический способ решения задач состоит в том, чтобы найти неизвестную величину составлением числовых выражений (числовых формул) и подсчета результата. Этот способ решения задач имеет важное методическое значение. Прочное усвоение методов решения задач арифметически позволяет подготовить учащихся к осознанному решению задач составлением уравнений.

Рассмотрим задачу: «Два велосипедиста выехали одновременно навстречу друг другу с одинаковой скоростью. Через какое время они встретятся, если расстояние между ними 60 км, а скорость 12 км/ч?»

Арифметически эту задачу можно решить так:

1. Какова скорость сближения велосипедистов?

12+12 = 24(км/ч).

2. Через какое время велосипедисты встретятся?

60:24 = 2,5(ч).

Ответ: велосипедисты встретятся через 2,5 часа.

Алгебраический способ основан на использовании уравнений и систем уравнений при решении текстовых задач. Известный американский педагог и математик Д. Пойа в своей книге по проблемам обучения решению задач пишет, что «составить уравнение – значит выразить математическими символами условие, сформулированное словами. Это перевод с обычного языка на язык математических формул. Трудности, которые могут встретиться при составлении уравнений, являются трудностями перевода». Это же в полной мере, на наш взгляд, можно отнести к записи решения выражением.

В данном пособии мы не будем затрагивать методику работы над решением задачи составлением уравнения, однако отметим, что в начальных классах за неизвестное обычно принимается то число, о котором спрашивается в задаче, и что уравнения решаются детьми только на основе связей компонентов и результатов арифметических действий.

Рассмотрим предыдущую задачу. Её решим алгебраически, но двумя способами:

1 способ:

Примем за х ч время, через которое встретятся велосипедисты, тогда, учитывая, что они двигались навстречу друг к другу с одинаковой скоростью 12 км/ч и прошли вместе 60 км можно составить уравнение: (12+12)х=60, где (12+12) км/ч – скорость сближения.

(12+12)х=60

24х=60

х=60:24

х=2,5 (ч)

Ответ: велосипедисты встретятся через 2,5 часа.

2 способ:

Примем за х ч время, через которое они встретятся. Тогда первый до встречи пройдет 12х (км) и второй тоже 12х (км). Так как вместе они прошли 60 км, то можно составить уравнение: 12х + 12х = 60.

12х+12х=60

24х=60

х=60:24

х=2,5 (ч)

Ответ: велосипедисты встретятся через 2,5 часа.

Графический способ решения представляет собой получение результата путем применения различных схем и геометрической интерпретации задачи.

Рассмотрим решение следующей задачи: «Из Сухуми и Ялты одновременно навстречу друг другу вышли два теплохода. Встретились ли они, если первый прошел 3/5 всего пути, а второй – 5/12 всего пути?»

Если весь путь изобразить произвольным отрезком СЯ, используя теорему Фалеса найти 3/5 этого отрезка, отложив ее от точки С, затем найти 5/12 этого же отрезка и отложить эту часть от точки Я, то можно решить задачу графически. В случае, когда полученные отрезки-части пересекутся, можно сделать вывод, что корабли встретились, в противном – нет. В данной задаче корабли встретились.

Решение задач графическим способом можно осуществлять и при помощи отрезков: «С первой грядки сорвали 4 огурца, а со второй 3 огурца. Сколько всего огурцов сорвали с двух грядок?»

Пересчитыванием можно найти ответ: 7 огурцов.

Практический способ решения предусматривает манипуляции с предметами, о которых говорится в задаче или с их изображениями и позволяет дать ответ на вопрос задачи, не выполняя при этом арифметических действий.

Например, рассмотрим задачу: « В коробке лежало 12 конфет. Мама дала дочери 2 конфеты и еще 2 конфеты сыну. Сколько конфет осталось в коробке?»

При решении этой задачи практическим способом можно выложить на парту 12 палочек, иллюстрирующих общее количество конфет, затем удалить сначала 2 палочки (2 конфеты дочке), а потом еще 2 палочки (2 конфеты сыну). Пересчитать остаток – 8 палочек (8 конфет). Этот результат и будет ответом задачи.

Практический способ решения задач очень важен при введении конкретного смысла арифметических действий, например, деления. Решение задач детьми-дошкольниками часто производится именно этим способом.

Н.Б. Истомина считает, что графический способ близок к практическому, но имеет более абстрактный характер и требует специальной подготовки учащихся [8, c.199].

Часто для решения задачи необходимо выделение (отбор) из данного множества некоторого подмножества, обладающего определенными признаками. Обычно такой отбор проводится в несколько этапов: при постепенном использовании данных задачи начинают выделять избыточное подмножество элементов, сужая его, отбирают требуемые, или показывают, что их нет. Метод отбора часто используется для решения комбинаторных задач.

Способ решения задачи подбором результата в каждом случае достаточно индивидуален, однако достаточно часто используется младшими школьниками при решении задач. На уроках не стоит запрещать детям решать задачи этим способом, однако лучше данный способ использовать для прикидки результата.

Рассмотрим применение подбора при решении задач в начальных классах.

Дана задача «На столе лежали 6 груш и 4 яблока. Саша взял со стола 5 фруктов. Сколько яблок и груш отдельно мог взять Саша?». При решении этой задачи можно рассуждать таким образом, основываясь на знании состава числа 5: Саша мог взять либо только яблоки, либо только груши (5=0+5=5+0). Тогда ответ будет или 5 яблок и 0 груш, или 0 яблок и пять груш. Дальше анализируются остальные случаи состава числа 5, формулируется ответ (5=1+4=4+1; 5=2+3=3+2).

Способ решения задачи при помощи схематического моделированияпозволяет получать решение задачи моделированием схемы отношений между данными и искомыми. Схема может выступать как способ решения задачи, так и как форма записи решения задачи [8, c.202].

Например: «На двух тарелках было по 18 яблок. На десерт из одной тарелки взяли несколько яблок, а из второй – столько, сколько осталось на первой тарелке. Сколько яблок осталось на двух тарелках?»

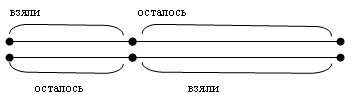
На основе данной схемы можно дать ответ на вопрос задачи: в двух тарелках осталось 18 яблок.

Схематическое моделирование позволяет при помощи пропорциональных отрезков изображать данные в задачах отношения. Именно этот способ, используемый в виде краткой записи, позволяет решать так называемые задачи «на части» в средних классах школы.

Кроме вышеперечисленных способов могут быть использованы различные их комбинации, т.е. комбинированный способ решения задачи.

Например, рассмотрим следующую задачу: «Один рабочий может выполнить работу за 4 ч, а другой эту работу может выполнить за 6 ч. Какую часть всей работы выполнит каждый рабочий, если они будут работать вместе?»

Решение:

Пусть весь объем работы составляет единицу. Тогда за 1 час первый рабочий выполнит 1:4=1/4 часть, а второй 1:6=1/6 часть всей работы. Время, за которое рабочие выполнят все задание при совместной работе, обозначим через х ч, тогда первый выполнит (¼)х часть всей работы, а второй (1/6 )х часть всей работы. Так как вся работа составляет единицу, составим уравнение:

1/4х+1/6х = 1

(¼+1/6)х = 1

х = 2 2/5 (ч).

Тогда первый рабочий выполнит ¼×2 2/5 = 3/5,

а второй – 1/6×2 2/5 =2/5.

Ответ: первый рабочий выполнит 3/5 всей работы, а второй – 2/5 всей работы.

В данной задаче сначала используется алгебраический способ решения, а потом – арифметический. Таким образом, задача решена комбинированным способом.

Рассмотрим следующую задачу: «Когда из портфеля вынули 6 тетрадей, в нем осталось в три раза меньше тетрадей, чем было. Сколько тетрадей было в портфеле?»

Решение:

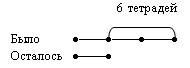
1) 6:2=3 (т.)

2) 3×3=9 (т.)

Ответ: было 9 тетрадей.

В данном решении комбинированы схематическое моделирование и арифметический способы решения задачи. Из модели видно, что на 6 тетрадей приходится две одинаковые части, значит можно найти, сколько приходится на одну часть, а дальше используется арифметический способ решения.

Упражнения

1. Решите задачу разными способами. Выберите самый рациональный. Обоснуйте свой выбор. «За 3 дня перевезли 540 т груза. В первый день перевезли 7/18 всего груза, во второй день – 4/18 его, а остальной груз был перевезен в третий день. Сколько тонн груза перевезли в третий день?» Выделите и последовательно сформулируйте простые задачи, которые вы решали в процессе решения исходной задачи.

2. Найдите в учебниках математики начальных классов или составьте самостоятельно, задачи, которые можно решить только при помощи схемы, либо комбинированным способом.

3. «Один рабочий может выполнить работу за 4 ч, а другой эту же работу может выполнить за 6 ч. Какую часть всей работы выполнит каждый рабочий, если они будут работать вместе?» Эту задачу можно решить арифметически в 2 действия. Попробуйте.

4. Даны задачи: а) В первый день магазин продал 8 одинаковых портфелей и получил за них 32 грн. Во второй день было продано 6 таких портфелей. Сколько денег получили за портфели во второй день? б) Построили 9 домов по 4 квартиры и 5 домов по 10 квартир. Сколько всего квартир построили? в) В шкафу стояло 6 глубоких тарелок, мелких в 3 раза больше, чем глубоких, а блюдец в 2 раза меньше, чем мелких тарелок. Сколько блюдец было в шкафу?

Решите эти задачи. Выберите из них задачи, в которых достаточно изменить одно число, чтобы задача могла быть использована для изучения свойств арифметических действий. Сделайте это.

5. Из задач предыдущего упражнения выберите ту, которая легко решается графически. Решите ее таким способом. Рассмотрите в учебнике Б2, М2 подряд 10 текстовых задач. Которые и сколько из этих задач могут быть решены графически? Как вы думаете, почему этот способ решения задач не часто практикуется на уроках? Согласны ли вы с этим? Почему?

6. Дана задача: «Из 100 л молока получается 4 кг масла. Сколько масла получиться при переработке 5000 л молока?»

Найдите не менее трех различных способов решения задачи. Каждое из решений запишите в виде выражения. Сравните полученные выражения. Найдите прием, который позволяет, зная один способ решения, найти остальные способы. При этом не путайте способы решения и способы записи решения. Зачем учителю знать всевозможные способы решения задачи?