На этом этапе основная цель – закрепить и обобщить у учащихся умение решать задачи данного вида. Обобщение позволяет охватить все возможные случаи решения данного вида задач в виде обобщенного алгоритма, значит, к целям этого этапа относится и формирование обобщенного алгоритма решения. Однако выделение связей в обобщенном алгоритме решения задач не должно подменяться зазубриванием последовательности действий. Выбор действий должен быть осознанным.

Для многих учащихся для обобщения решения задач того или иного вида достаточно выделить опорную задачу, в процессе обучения решению которой они «с места» (В.А. Крутецкий) анализируют принципы решения этой задачи и переносят на другие задачи данного вида. Таким образом, уже на первой типовой задаче учащиеся усваивают всю необходимую информацию об особенностях задач данного вида, т.е. подводят их решение под обобщенный способ действия.

Однако чаще всего обобщение происходит при постепенном усложнении задач, при этом решение достаточного количества задач данного вида традиционно в школе многие учителя проводят сначала массированно, потом – вперемежку с задачами других видов. Этот прием, на наш взгляд, приводит к тому, что часто дети решают задачи формально, по аналогии с предыдущими задачами. Поэтому на этом этапе имеет смысл использовать другие приемы, например, методику работы с обратными задачами П.М. Эрдниева (частичное или полное обращение задач), рассмотрение пар задач разных видов, которые дети часто путают, деформацию и трансформацию задач, и другие виды последующей работы над задачами.

В учебниках и дидактических материалах задачи часто приводятся в парах или тройках. Рассмотрим пару задач:

1. Для живого уголка купили 10 рыбок и посадили их в аквариумы парами. Сколько потребовалось аквариумов?

2. Для живого уголка купили 10 рыбок и посадили их в два аквариума поровну. Сколько рыбок посадили в каждый аквариум?

Решим сначала первую задачу.

Краткая запись: по 2 рыб. – ? акв. – 10 рыб.

Решение: 10:2=5 (акв.)

Ответ: потребуется 5 аквариумов.

Решим вторую задачу.

Краткая запись: по ? рыб. – 2 акв. – 10 рыб.

Решение: 10:2=5 (рыб.)

Ответ: в каждом аквариуме по 5 рыбок.

После решения каждой из этих задач следует провести полное сравнение их условий, кратких записей, решений и ответов. В данном случае в паре даны задачи на деление по содержанию (1) и деление на равные части (2). Одна из целей рассмотрения этих задач в паре – показать, что задачи на разные виды деления («на» и «по») решаются одним и тем же действием деления.

К сожалению часто учителя предлагают детям упражнения с такими парами задач для решения на самостоятельной работе по вариантам (первый вариант – первая задача, второй вариант – вторая), или одну задачу решают в классе, а вторую задают в качестве домашнего задания, нарушая тем самым дидактический замысел.

Проиллюстрируем закрепление навыков решения задач одного вида. При закреплении решения простых задач на увеличение числа на несколько единиц можно сначала закрепить решение на готовых текстах задач.

Например: «У курицы было 7желтых цыплят, а серых на 3 больше. Сколько серых цыплят было у курицы?»

Далее можно использовать прием полного обращения данной задачи (т.е. составить и решить все задачи, обратные данной). Это позволит учащимся наиболее выпукло рассмотреть все связи в задаче.

Также можно использовать прием составления аналогичной задачи по краткой записи.

«Составь задачу по краткой записи и реши ее:

1 полка – 6 книг

2 полка – ?, на 4 больше»

Далее можно использовать прием деформации задачи по одному из чисел, по двум числам:

«Подставляя числа в окошечко, составь задачи и реши их: «Высота яблони  м, а вишни на š м больше. Какова высота вишни?»»

В этой задаче на числа для «окошек» должны быть наложены ограничения (высота деревьев ограничена).

Еще раз подчеркиваем, что следует учитывать индивидуальные особенности восприятия каждого из учеников при переходе к этапу закрепления, некоторые дети после первых объяснений не нуждаются в дальнейшей помощи со стороны учителя, другие воспринимают все в более низком темпе. Поэтому, тщательно должны быть продуманы задания для каждой из групп детей.

Проверить сформированность обобщения решения задач данного вида можно при помощи критериальных задач (задачи, выступающие критерием сформированности нужного обобщения). Однако, умение решать конкретные видовые задачи еще не является свидетельством сформированности у ученика обобщенного решения задач данного вида, т.к. в силу конкретности этих задач это умение выступает лишь косвенным признаком сформированности обобщенного алгоритма решения. Значит, наряду с конкретными задачами данного вида детям необходимо предлагать задачи с обобщенными данными (задачи, составляющие класс конкретных задач, исключающие частные признаки (числовые данные) в этих задачах). К обобщенным задачам можно отнести деформированные задачи, задачи с переменными. Правильное решение таких задач позволяет сделать вывод о сформированности обобщения.

Например, при закреплении навыков решения простых задач можно использовать следующие упражнения:

1) Рассмотри краткую запись задачи.

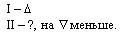
Из предложенных далее кратких записей задач, выбери задачи, обратные данной, если ее ответ обозначен

Подумай, есть ли среди предложенных задач взаимообратные задачи. Ответ объясни.

2) Схема решения задачи выглядит так: +Ñ=◄.

При помощи схем изобрази решения обратных задач.

3) В коробке  карандашей, а в пенале на ▲ больше. Сколько карандашей в коробке и пенале вместе? Запиши решение задачи выражением-схемой. Подбери числа. Найди значение выражения. И т.д.

4) Работа над тройкой задач.

а) Во вторник Боря смастерил 6 игрушек на елку, а в среду 5 игрушек. Сколько игрушек смастерил Боря за два дня?

б) Во вторник Саша смастерил 3 игрушки на елку, а в среду 7 игрушек. Сколько игрушек смастерил Саша за два дня?

в) Во вторник мальчик смастерил a игрушек на елку, а в среду b игрушек. Сколько игрушек смастерил мальчик за два дня?

В соответствии с требованиями программы, современные методисты не рекомендуют учителям сообщать детям название типов и видов задач, так как считается, что это мешает развитию логического мышления учащихся (М.В. Богданович, М.А. Бантова, В.Л. Дрозд и др.). Хотя названия все-таки вводятся по желанию учителя, иногда под другими, более простыми названиями или под номерами. Однако, существует и противоположное мнение: некоторые методисты считают это нарушением принципа историзма в преподавании математики. Например, П.М. Эрдниев и Б.П. Эрдниев пишут, что в программах для четырехлетней начальной школы отказались от традиционных названий трех видов задач (увеличение на несколько единиц, уменьшение на несколько единиц, разностное сравнение) и заменили их упрощенным «больше – меньше на», однако, такой термин не охватывает главного вида задач на «разностное сравнение» [18].

На наш взгляд, каждый учитель вправе сам решать вопросы, связанные с сообщением названий видов задач учащимся, т.к. действующей программой это не предусматривается.

Упражнения

1. При изучении задач нового вида учитель может использовать разные формы ознакомления с ее содержанием: учитель сам читает текст задачи вслух; предлагает детям самостоятельно прочитать задачу; предлагает детям составить задачу по краткой записи; предлагает детям получить ее путем трансформации уже знакомой детям задачи и т.д. Какие еще способы знакомства с содержанием задачи вы знаете? Проанализируйте достоинства и недостатки каждого способа. От чего зависит выбор способа знакомства с содержанием задачи? Есть ли среди способов те, которые следует предпочесть остальным? Почему?

2. Рассмотрите приведенную группу задач. Определите вид каждой задачи. Решите. Объясните, почему они сгруппированы вместе.

а) В двух коробках 36 карандашей. В одной из них 24 карандаша. Сколько карандашей во второй коробке?

б) Марина подписала 23 поздравительных открытки, и ей еще осталось подписать 9 открыток. Сколько открыток должна подписать Марина?

в) Одна бригада штукатуров обработала 21 дом, а другая 15. На сколько домов больше обработала первая бригада, чем вторая?

г) В магазин привезли 35 ящиков с кефиром, на 7 ящиков меньше, чем с молоком. Сколько ящиков с молоко привезли в магазин?

3. Найдите в учебниках Б1, Б2, Б3 задачи, приведенные в группе (паре, тройке и т.д.). Проанализируйте эти задачи. Какова цель их использования. Какую работу вы предлагаете провести над ними?

4. Дана пара задач:

а) Закройщица раскроила 8 платьев. Половину этих платьев портниха уже сшила. Сколько платьев сшила портниха?

б) Портниха сшила 8 платьев. Это половина платьев, которые раскроила закройщица. Сколько платьев было раскроено?

Учитель предлагает решить и сравнить эти задачи: «Чем похожи и чем отличаются содержание? Решения? Ответы?» После сравнения делает выводы. Проведите это сравнение подробно, с предполагаемыми ответами детей.

5. Дана задача: «Настольная лампа стоит 6 грн., а люстра на 24 грн. дороже. Во сколько раз дороже стоит люстра, чем лампа?» Дети решили задачу так: 24:6=4. Проанализируйте причину такой ошибки. Составьте парную задачу для сравнения и проведите сравнение.

6. Дана задача: «Машина за 4 часа вырыла 140 м канавы. Сколько времени ей понадобится, чтобы при той же производительности труда вырыть 210 м канавы?» Учитель предложил детям такое упражнение: «Измените одно из чисел в этой задаче так, чтобы ответ увеличился; уменьшился; уменьшился в два раза. Почему так происходит?» С какой целью может быть применено в начальных классах такое упражнение? Составьте подобные упражнения к задачам из предыдущего задания. Проведите языковой анализ задачи, разбейте ее текст на смысловые ситуации. Как вы думаете, какие трудности могут возникнуть у учащихся при анализе текста и решении этой задачи?