С точки зрения не математика хочется назвать простой задачу, которая кажется легкой в решении и, по этой ассоциации, кажется, что другие задачи будут сложными.
Однако математики делят задачи на простые и составные (сложные) по другому признаку: количеству выполняемых арифметических действий. Простой называют задачу, которая решается при помощи одного действия, а под составной понимают задачу, в решении которой используют два или более действий.
Если в задаче нельзя выделить другую задачу, то это простая задача, если можно – то составная (сложная) задача. Составную задачу можно разложить на простые или составные подзадачи, решение которых приводит к решению основной составной задачи. Разложение составной задачи на простые не всегда однозначно [19, c. 177]. Это означает, что задачи можно решать различными способами.
Например, рассмотрим следующие задачи:
1. Какова скорость велосипедиста, если за 5 часов он проехал 75 км?
Решение:
1) для того, чтобы найти скорость движения на данном отрезке пути нужно величину пути 75 км разделить на время, затраченное на его прохождение 5 часов.
75:5 = 15 (км/ч).
Ответ: скорость велосипедиста 15 км/ч.
2. Попадет ли за 8 часов велосипедист из деревни в город, расстояние до которого 120 км, если за 5 часов он проезжает 75 км?
Решение:
1) Какова скорость велосипедиста на данном этапе пути?
75:5= 15 (км/ч).
2) Какой путь проедет велосипедист за 8 часов?
15×8 = 120 (км/ч).
Ответ: т.к. за 8 часов велосипедист проедет 120 км, то в город, до которого расстояние 120 км, за это время он успеет добраться.
Первая задача является простой, так как решается одним действием, а вторая – решается несколькими действиями и является составной.
В системе задач, рассматриваемых в школьном курсе математики, существует классификация простых задач и составных задач по разным признакам (см. далее).
Упражнения
1. Выберите из предложенных задач простые задачи и решите их. Составные задачи разбейте на простые. Сформулируйте условие и вопрос каждой простой задачи, входящей в данную составную.
§ На двух делянках росло 807 роз. Когда с первой делянки срезали 167 роз, то на ней осталось 123 розы. Сколько роз росло на каждой делянке?
§ Мама купила 2 десятка груш. Сын съел пятую часть всех груш. Сколько груш осталось?
§ Петя купил 3 открытки, а Алина в 2 раза больше. Сколько открыток купила Алина?
§ Из двух городов, расстояние между которыми 280 км, одновременно навстречу друг другу выехали два автобуса. Один со скоростью 60 км/ч, а второй – 70 км/ч. На каком расстоянии друг от друга они находились через час?
2. Найдите в методической литературе не менее трех различных методических подходов к первому знакомству с составной задачей. Какой из них вам больше нравится. Почему? Составьте серию подготовительных упражнений для первого знакомства с составной задачей, соответствующую выбранному вами подходу. Подумайте, что пришлось бы изменить в составленной серии, если бы вы выбрали другой подход.
Понятие задач одного вида
Л.М. Фридман, Е.Н. Турецкий в школьном курсе математики выделяют следующие виды задач, отвечающие таким признакам:
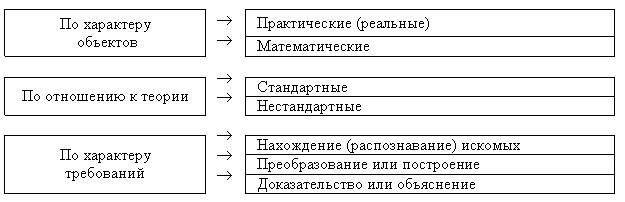
Классификация простых и составных задач, решаемых в начальной школе, производится по признаку отношения к теории, т.е. задачи подразделяются на стандартные и нестандартные. Некоторые методисты называют эти задачи соответственно алгоритмическими и эвристическими. При этом стоит отметить, что данное деление является условным, в связи с тем, что любая из задач может содержать как стандартный, так и нестандартный (творческий) компонент.
Математические задачи, для решения которых в школьном курсе математики имеются готовые правила (в виде словесного алгоритма, формулы, тождества и т.д.) или эти правила непосредственно следуют из правил, теорем, определений программного минимума называют стандартными. При этом предполагается, что для решения этих задач имеются вполне определенные правила-алгоритмы (отсюда – алгоритмические).
Начальный курс математики содержит в себе несколько основных групп задач, решение которых основывается на одних и тех же связях между данными и искомым, а отличаются лишь конкретными числовыми данными и сюжетом (стандартные). Именно эти группы задач методисты начальной школы называют задачами одного вида.
Вообще задачи, связанные между собой таким образом, можно называть стандартными, задачами одного вида (видовыми) или задачами одного типа (типовыми). Однако, часто термин «тип» используется как собирательный для нескольких видов задач.
Например, задачи на четвертое пропорциональное (тип) подразделяются на 6 видов (Бантова М.А., Бельтюкова В.Г.), которые в других источниках называют видом и подвидами, поэтому имеет смысл внимательно просматривать сам первоисточник, чтобы определиться со смыслом используемой терминологии.
Приведем пример задач одного вида.
1. В одной коробке 6 карандашей, во второй – в 3 раза больше. Сколько карандашей в двух коробках вместе?
2. В первом аквариуме 8 рыбок, а во втором – в 2 раза больше. Сколько рыбок в двух аквариумах?
Данные задачи отличаются сюжетом: в первой речь идет о карандашах в коробках, а во второй – о рыбках в аквариумах. Числовые данные в данной ситуации тоже различны, однако обе задачи имеют одинаковую теоретическую основу – увеличение в несколько раз и нахождение численности объединения двух непересекающихся множеств. По способу решения они имеют один алгоритм – сначала требуется найти, сколько предметов во втором случае, а потом – сколько вместе. Поэтому их можно назвать задачами одного вида.
Упражнения
1. Какие задачи называют стандартными? Приведите примеры стандартных задач.
Дата: 2018-12-28, просмотров: 1712.