Первое знакомство с задачей состоит из трех этапов: подготовительного, основного и закрепления.
Существуют два основных подхода к ознакомлению с задачами.
Первый подход предусматривает одновременное ознакомление с задачей (понятие задачи, ее составные части, работа с памяткой и т.д.) и формирование конкретного смысла действий сложения и вычитания (Богданович М.В., Моро М.И., Бантова М.А. и др.) и является традиционным для действующей программы. В основном, на первых порах, проводится устная работа над задачей, так как дети в этот период обучения медленно читают и пишут. На наш взгляд, данный подход соответствует требованиям современного математического образования. Зачем от детей «прятать» понятие «задача»? Задачи, как таковые, решаются детьми еще в детском саду, где их целенаправленно учат выделять условие и требование задач (см. Математическая подготовка детей в дошкольных учреждениях / Р.Л.Березина, В.В. Данилова, Т.Д. Рихтерман и др.; Сост. В.В. Данилова. – М.: Просвещение, 1987. – 175 с.).
Рассмотрим второй подход.
Этот подход используют практически все авторы учебников развивающего обучения. Процесс решения задач рассматривается с точки зрения моделирования:
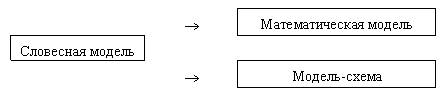
На подготовительном этапе ознакомление с задачей должно проходить при помощи задач-действий с предметными множествами, операций по объединению этих множеств и удалению их частей (Истомина Н.Б., Аргинская И.И. и др.). До знакомства с задачей у учащихся должны быть сформированы логические приемы мышления, сформированы непосредственно математические понятия и отношения, которые будут использоваться при решении задач.
Готовность школьника к знакомству с текстовой задачей включает в себя сформированность следующих компонентов (СНОСКА: Подробнее см. Истомина Н.Б., Нефедова И.Б. Первые шаги в формировании умения решать задачи. Новые подходы в обучении // Начальная школа.- 1998.- № 11-12. – С. 42-48)
1. умения читать;
2. четкой сформированности понятий сложения и вычитания, а также умения «переводить» на математический язык сюжетов задач;
3. сформированности приемов умственных действий (анализ, синтез, сравнение, аналогия, обобщение);
4. умения работать с различными моделями задачи: текстовой, предметной, схематической и символической.
Таким образом, формирование вышеперечисленных навыков и приемов и представляет собой подготовительную работу к первому знакомству с задачей и ее решением. В связи с этим ознакомление с задачей по программам развивающего обучения происходит значительно позже, чем по традиционным программам (1-3), практически только к концу первого года обучения.
На наш взгляд, при использовании данного подхода к введению задач нарушается последовательность и преемственность в дошкольном и начальном школьном обучении. Искусственно сдерживается возможность дальнейшего роста учащихся, подготовительные задания, несмотря на их необходимость, затягивают изучение материала. Однако, на наш взгляд, при обучении в соответствии с типовыми программами необходимо учитывать вышеперечисленные компоненты готовности учащихся к первому знакомству с задачей, но развивать их параллельно с работой над задачами, считая их развитие одним из направлений этой работы.
Что значит решить задачу?
В начальный период знакомства с задачами чаще всего дети понимают, как дать ответ на поставленный в задаче вопрос (знают число). В случае, когда решается задача в одно действие, дети сразу после сообщения текста задачи учителем дают ответ на вопрос, не отвечая при этом, откуда этот ответ взялся («Подумал», «Догадался», «Посчитал», «Не знаю»), и если учитель говорит, что данное решение нельзя принять, дети обижаются. Поэтому следует четко провести грань между загадкой и задачей.
На первый взгляд может показаться, что вопрос «Что значит решить задачу?» не нуждается в обсуждении. Это не так. Термин «решение задачи» употребляется в достаточно большом наборе различных ситуаций из жизни и в учебном процессе.
Можно рассматривать только два аспекта (Истомина Н.Б.):

Три аспекта термина «решение задачи» рассматривают Л.М. Фридман и Е.Н. Турецкий:

Остановимся на последней схеме. Если принять за основное первое толкование термина «решение задачи» (вся деятельность…), то выделяются следующие этапы решения задачи:
а) ознакомление с содержанием задачи, анализ содержания задачи;
б) составление краткой записи, схемы задачи;
в) поиск способа решения задачи, составление плана;
г) выполнение плана решения задачи;
д) проверка полученного решения;
е) исследование задачи;
ж) формулировка ответа к задаче;
з) последующая работа над задачей.
Данная схема не является догмой, более того, практически все ее этапы, учитывая реальный процесс мышления, взаимопроникают друг в друга. Например, анализ содержания задачи в неявной форме представляет собой не что иное, как неявную форму поиска решения.
К способам ознакомления с содержанием задачи относятся:
а) чтение задачи учеником;
б) восприятие задачи на слух (чтение задачи учителем или учащимся);
в) составление задачи по опоре (краткой записи, иллюстрации, инсценировке, схеме и т.д.);
г) трансформация задачи (из решенной задачи составляется новая) и т.д.
Для того чтобы решить задачу, ученик должен уметь выполнять следующую последовательность переходов:
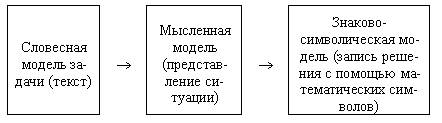
Каждая из моделей описывает единственный объект – задачу. Выполнены они на разных языках: языке слов, языке образов и языке математических символов. Для построения любой из этих моделей учащийся должен выделить только существенные свойства объектов и структуру связей и отношений между ними. Для математической модели – выделить количественные соотношения предложенной в задаче ситуации и связи между данными и искомым. Первый и второй пункты данной схемы относятся к этапу ознакомления с содержанием задачи.
На основе вышеперечисленного составляется «Памятка по решению задачи» (№ 1) для учеников начальных классов.
Памятка по решению задачи
1. Прочитай задачу, представь то, о чем говорится в задаче.
2. Запиши задачу кратко, если необходимо, сделай чертеж или схему.
3. Объясни, что показывает каждое число и назови вопрос задачи.
4. Подумай, какое число должно получиться в результате (например, больше или меньше, чем данные числа и т.д.)
5. Подумай, можно ли сразу ответить на вопрос задачи. Если нет, то почему? Что нужно узнать сначала? Что потом? Составь план решения задачи.
6. Выполни решение.
7. Проверь ответ и ответь на вопрос задачи.
8. Подумай, можно ли решить задачу другим способом?
9. Подумай, при каких условиях ответ задачи получился бы больше? Меньше?
Разумеется, можно варьировать последовательность вопросов в данной памятке в зависимости от конкретных условий, учитывать их взаимопроникновение.
Рассмотрим работу над следующей задачей «Из молока получается 10% творога. Сколько творога получится из 32,8 кг молока?» (задача для 5 класса).
Данная задача часто с трудом решается детьми, которые не представляют себе процесс производства творога. Поэтому после чтения условия задачи можно спросить детей, знают ли они, как делают творог, какие еще продукты получаются из молока при изготовлении творога (сыворотка). В данной ситуации не стоит жалеть времени на информацию о производстве творога, ведь это не только способствует решению данной конкретной задачи, но повышению общего уровня развития ребенка.
Далее следует поработать над фразой «Из молока получается 10% творога». Как вы это понимаете? Из какого количества молока получается 10% творога? (Из любого, т.е. из чайной ложки, 1 кг, 1 т и т.д.).
Масса полученного творога должна быть меньше или больше массы молока? (Меньше, т.к. творог получается из веществ, которые являются составной частью молока).
Краткую запись задачи можно сделать несколькими способами, желательно выбирать тот способ, который позволит облегчить поиск решения. Приведем примеры:
1)
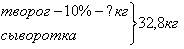
2) 10% от 32,8 кг – ?кг

3)
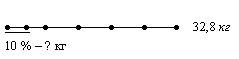
Кроме приведенных примеров, это могут быть и другие схемы, чертежи, рисунки, картинки и т.д. (все зависит от индивидуальных особенностей восприятия каждого ученика). Главное, чтобы при этом ребенок понял, о чем говорится в задаче.
Итак, что мы знаем из условия задачи? (У нас есть 32,8 кг молока, нужно найти, сколько творога получится из этого количества молока или, согласно условию задачи, 10% от 32,8 кг).
От какого числа следует найти 10 % в задаче? Как найти 10% от 32,8 кг? (32,8 кг разделить на 100% и результат умножить на 10).
Запишем решение
32,8:100×10=3,28 (кг).
Ответ: из 32,8 литра молока получится 3,28 кг творога.
Можно ли записать решение задачи по-другому? Как вы понимаете 10 % от чего-либо? (Десятая часть, десять сотых данного числа). Как найти 10 % или десятую часть от числа? (Разделить на 10; умножить на 0,1).
1 способ: 32,8:10=3,28 (кг);
2 способ: 32,8×0,1=3,28 (кг).
Если рассматривать термин «решение задачи» только как процесс нахождения ответа, то изменится только количество выделяемых этапов. В этом случае будем считать, что:
Решить задачу (в узком смысле) – не только дать ответ на вопрос задачи (назвать результат), но и объяснить, какие действия нужно выполнить над данными в ней числами, чтобы получить после вычислений искомое число или результат, либо доказать, что решения не существует, либо обозначить отношение, о котором спрашивается в задаче.
Записать решение задачи (если речь идет о конкретных числах) –при помощи цифр и знаков действий показать, что нужно сделать, чтобы найти неизвестное число, выполнить все эти действия и дать ответ на вопрос задачи.
С точки зрения данного подхода для решения задачи необходимо действовать по следующему плану:
а) раскрыть связи между данными и искомыми;
б) на основе этих связей выбрать действия для решения;
в) выполнить эти действия;
г) дать ответ на вопрос задачи.
Как видим, не проводится работа по проверке решения, последующая работа над задачей, однако, работа по чтению задачи, составлению плана решения подразумевается.
В данном случае используется следующая «Памятка по решению задачи» (№ 2):

Например, рассмотрим решение следующей задачи (на основе Памятки №2):
«За 5 метров ткани заплатили 30 гривень. Сколько стоит 1 метр этой ткани? (Какова цена ткани?)»
Прочитайте задачу. Повторите условие задачи. (За 5 метров ткани заплатили 30 гривень). Повторите вопрос задачи. (Сколько стоит 1 метр этой ткани?)
а) Если за 5 метров ткани уплатили 30 гривень, то за 1 метр нужно уплатить больше или меньше? (Меньше). Во сколько раз? (Нужно уплатить меньше в 5 раз).
б) Чтобы найти величину в 5 раз меньшую, чем 30 гривень, какое действие нужно выполнить? (Нужно 30 гривень уменьшить в 5 раз, значит, разделить на 5). Следовательно, задача решается действием деления.
в) Решение: 30:5 = 6 (грн.)
г) Ответ: цена ткани 6 гривень.
Работа по памятке №2 помогает детям полнее осознать понятие «задача», учит выделять ее составные части задачи и решение.
В дальнейшем, для работы над задачами целесообразно использовать конструктивную памятку, которая учит детей объяснять каждый шаг в решении задачи.

Проиллюстрируем работу по конструктивной памятке на конкретной задаче.
«На столе 5 карандашей, а в коробке на 2 больше. Сколько карандашей в коробке?»
Записи на доске и в тетрадях детей появляются в процессе работы по конструктивной памятке.
Известно. На столе 5 карандашей, а в коробке на 2 больше.
На доске появляется запись:
5 2
Спрашивается. Сколько карандашей в коробке (вместо вопроса ставится точка, т.к. эту запись в дальнейшем трансформируем в запись решения задачи).
5 2
Объясняю. Так как в коробке карандашей больше на 2, чем на столе, то буду выполнять сложение (в записи появляется знак «+»).
5 + 2
Решаю. К 5 карандашам прибавить 2 карандаша будет 7 карандашей (в записи появляется результат вычисления и наименование).
5 + 2 = 7 (кар.)
Ответ: 7 карандашей в коробке.
Работа над задачей, организованная таким образом позволяет ребенку использовать речевой образец, сначала вслух, а затем про себя.
Упражнения
1. «Масса сушеных яблок составляет 16% массы свежих яблок. Сколько надо взять свежих яблок, чтобы получить 4 тонны сушеных? Сколько сушеных яблок получится из 4,5 тонн свежих яблок?»
Проанализируйте задачу, решите ее в соответствии с памяткой №1, конструктивной памяткой. Подумайте, какие трудности могут возникнуть во время работы над содержанием задачи. Предложите различные формы краткой записи. Какой вам кажется наиболее удобным? Почему?
2. Дана задача: «Утром на элеваторе было 96 т пшеницы. К полудню привезли еще пшеницу на трех машинах по 3 т на каждой. Сколько тонн пшеницы осталось на элеваторе, когда 3/5 всей пшеницы отправили на мельницу?»
Рассмотрите различные способы иллюстрации этой задачи.
а)
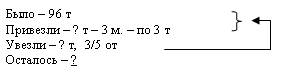
б)
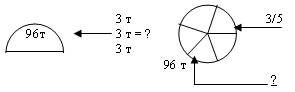
в)
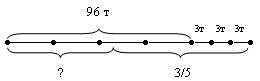
Какой из данных способов иллюстрации кажется вам более удачным? Почему? Какой способ предложили бы вы? От чего зависит выбор способа иллюстрации задачи?
3. Дана задача: «Вертолет за 2 часа пролетел 480 км. Сколько километров пролетит за 5 часов самолет, если его скорость в 3 раза больше скорости вертолета?» Проиллюстрируйте эту задачу различными способами. Нарисуйте словесную картину того, что происходит в задаче. Разбейте текст задачи на смысловые ситуации. Надо ли учителю иллюстрировать задачу по-разному?
Дата: 2018-12-28, просмотров: 717.