Оглавление
Введение. Роль и функции текстовых задач в обучении математике
Понятие текстовой арифметической задачи
Структура текстовой задачи
Различные методические подходы к первому знакомству с задачами
Что значит решить задачу?
Понятие простой и составной задачи
Понятие задач одного вида
Основные приемы работы над задачами одного вида
Этап подготовки к введению задач данного вида
Этап ознакомления с задачами данного вида
Этап закрепления умений решать задачи данного вида
Способы решения текстовых задач
Основные этапы решения задач
Изучение текста задачи и его анализ
Поиск способа решения
Краткая запись и другие виды графической работы с задачей
Синтетический и аналитический методы решения задач
Способы рассуждений при разборе задач
Решение задачи, способы записи арифметического решения задачи
Проверка решения задачи
Последующая и творческая работа над задачами
Развивающие функции задач в обучении математике в начальных классах
Задачи с недостающими или избыточными данными, нереальные задачи
Работа над деформированными задачами
Формы организации учебно-познавательной деятельности учащихся при работе над задачами
Дифференцированная работа над задачей
Различные подходы к типологии учащихся при организации уровневой дифференциации при работе над задачами
Дифференцированная работа над краткой записью задачи
Дифференцированная работа над задачами нового вида
Дифференцированная работа на этапе закрепления навыков решения задач данного вида
Приемы дифференцированной помощи при самостоятельной работе над текстовой задачей
Дифференцированная работа над задачей при проверке домашнего задания
Вопросы и указания для самостоятельной работы
Вопросы для самоконтроля
Тестовые задания
Список использованной литературы
Основная литература
Дополнительная литература
Учебники математики для начальных классов
Структура текстовой задачи
Любая задача состоит из предметной области, отношений, которые связывают объекты этой области, требования задачи и оператора (решения).
Под предметной областью понимают множество рассмотренных в задаче объектов, которые вместе со связывающими их отношениями образуют условие задачи.
Требование задачи – то, что необходимо найти в результате ее решения.
Под оператором задачи понимают совокупность действий, которые необходимо выполнить в соответствии с условием задачи над ее данными [3, c.7].
Например: «На уроке труда использовали 25 листов бархатной бумаги и 4 листа гофрированной бумаги. Сколько всего листов бумаги использовали на уроке?»
Предметная область данной задачи состоит из листов бархатной бумаги, листов гофрированной бумаги, из общего количества листов бумаги. Элементы этой предметной области связаны в данной задаче отношением суммы количества листов каждого вида. Известны следующие числовые характеристики предметной области: количество листов бархатной бумаги и количество листов гофрированной бумаги. Неизвестным выступает общее количество листов.
С множествами, составляющими предметную область, их числовыми характеристиками можно проводить следующую работу:
§ Перечисли все, что известно в задаче. (Известно, что израсходовали 25 листов бархатной бумаги и 4 листа гофрированной бумаги).
§ Перечисли все, что в задаче неизвестно. (Неизвестно, сколько всего листов бумаги израсходовали).
В начальной школе в текстовой задаче выделяют условие и требование (вопрос).
Без вопроса задачи нет. В результате решения задачи должно быть найдено искомое число (числа), либо показано, что такого числа не может быть (задачи с некорректными данными), либо установлены связи или отношения между числами. Этот результат получается при использовании числовых данных из условия, либо, если условие задачи не содержит явных числовых данных, из анализа условия.
Таким образом, в задаче должны быть данные и указаны зависимости между ними, причем эти зависимости могут быть указаны как прямо, так и косвенно.
Итак, в условии задач содержатся сведения о величинах известных и неизвестных, указываются связи и отношения между ними. В требовании содержится указание того, что нужно найти.
Требование может быть сформулировано в виде вопросительного или повелительного предложения, а так же может содержаться в условии задачи, при этом усложняется анализ содержания задачи, требуется переформулировка текста задачи. Одна и та же задача может быть сформулирована по-разному, например:
1. Два велосипедиста выехали одновременно навстречу друг другу из двух поселков, расстояние между которыми 76 км. Они встретились через 2 часа, причем, скорость одного из них больше скорости другого на 3 км/ч. Какова скорость каждого из велосипедистов?
2. Два велосипедиста выехали одновременно навстречу друг другу из двух поселков, расстояние между которыми 76 км. Они встретились через 2 часа, причем, скорость одного из них меньше скорости другого на 3 км/ч. Найдите скорость каждого из велосипедистов.
3. Два велосипедиста выехали навстречу друг другу из двух поселков, расстояние между которыми 76 км. Через 2 часа они встретились. Какова скорость каждого из них, если известно, что скорость одного на 3 км/ч меньше скорости другого?
Все три задачи являются различными формулировками одной. В первом случае условие и требование разделены, и требование сформулировано в вопросительной форме. Во втором случае требование сформулировано в повелительной форме. В третьем случае в требовании содержится часть условия. Кроме того, в первой задаче указано, что скорость одного больше скорости другого на 3 км/ч, а во второй и третьей – что скорость одного меньше скорости другого на 3 км/ч. Действительно, если один из них движется быстрее на 3 км/ч, то другой – медленнее на столько же км/ч.
Иногда «условием задачи» называют весь текст задачи, включая непосредственно условие и требование. Однако, с точки зрения методики, это не корректно. Учащихся необходимо учить читать текст (формулировку) задачи, выделять условие задачи и требование задачи в этом тексте.
Обратите внимание на то, что часто формулировки задач не содержат нужной информации, без которой нельзя говорить о функциональной зависимости или связях между величинами. Например, рассмотрим задачу: «За 6 чашек заплатили 19 грн. 20 коп. Сколько стоит одна чашка?» Для решения этой задачи необходимо все-таки выяснить одинаковые ли чашки, либо одинаковая ли у них цена. Иначе задача просто не имеет однозначного решения. Корректнее было бы сформулировать эту задачу так: «За 6 одинаковых чашек заплатили 19 грн. 20 коп. Сколько стоит одна чашка?» или «Купили 6 чашек по одинаковой цене. За всю покупку уплатили 19 грн. 20 коп. Сколько уплатили за каждую чашку?»
Упражнения
1. Выделите в данной задаче предметную область, отношение, требование задачи и оператор: «В парке посадили 130 берез и 150 лип. Сколько всего деревьев посадили?»
2. Выделите в данных задачах условие, требование, переформулируйте задачу различными способами: а) «Пешеход прошел за 6 ч 24 км. Сколько километров проедет машина за такое же время, если она поедет в 15 раз быстрее?»; б) «На 16 грузовиках перевезли 4000 ящиков с помидорами. Сколько таких ящиков перевезут на 48 таких же грузовиках?»; в) «Два шофера получили задание: за сутки перевезти с поля 43600 кг картофеля. Одна машина совершила 9 поездок, а другая – 7. Первая машина за один раз перевозила 1500 кг, а вторая – вдвое больше. Выполнили ли шоферы задание?» (СНОСКА: Задачи взяты из учебника [A3]) Подумайте, на какие неточности в формулировках задач нужно обратить внимание учащихся, чтобы задачи имели корректное решение.
3. Определите вид функциональной зависимости, которую можно пронаблюдать в каждой из задач. Предложите упражнение для такого наблюдения. а) «В 5 одинаковых клетках помещается 20 кроликов. Сколько нужно таких клеток, чтобы поместить в них 36 кроликов?»; б) «За 3 м бархата уплатили столько же, сколько за 14 м полотна. Цена бархата 28 грн. за метр. По какой цене покупали полотно?»
4. Даны две задачи: «Газета стоит 30 к., она дешевле журнала в 10 раз. Сколько стоит журнал?» и «Книга стоит 9 грн., а журнал в 3 раза дешевле. Сколько стоит журнал?» Выделите соответствия, присутствующие в задачах, сформулируйте обратные соответствия. Укажите задачу, в которой обратное соответствие используется для анализа задачи. Составьте подготовительное логическое упражнение или игру к этим задачам.
Что значит решить задачу?
В начальный период знакомства с задачами чаще всего дети понимают, как дать ответ на поставленный в задаче вопрос (знают число). В случае, когда решается задача в одно действие, дети сразу после сообщения текста задачи учителем дают ответ на вопрос, не отвечая при этом, откуда этот ответ взялся («Подумал», «Догадался», «Посчитал», «Не знаю»), и если учитель говорит, что данное решение нельзя принять, дети обижаются. Поэтому следует четко провести грань между загадкой и задачей.
На первый взгляд может показаться, что вопрос «Что значит решить задачу?» не нуждается в обсуждении. Это не так. Термин «решение задачи» употребляется в достаточно большом наборе различных ситуаций из жизни и в учебном процессе.
Можно рассматривать только два аспекта (Истомина Н.Б.):

Три аспекта термина «решение задачи» рассматривают Л.М. Фридман и Е.Н. Турецкий:

Остановимся на последней схеме. Если принять за основное первое толкование термина «решение задачи» (вся деятельность…), то выделяются следующие этапы решения задачи:
а) ознакомление с содержанием задачи, анализ содержания задачи;
б) составление краткой записи, схемы задачи;
в) поиск способа решения задачи, составление плана;
г) выполнение плана решения задачи;
д) проверка полученного решения;
е) исследование задачи;
ж) формулировка ответа к задаче;
з) последующая работа над задачей.
Данная схема не является догмой, более того, практически все ее этапы, учитывая реальный процесс мышления, взаимопроникают друг в друга. Например, анализ содержания задачи в неявной форме представляет собой не что иное, как неявную форму поиска решения.
К способам ознакомления с содержанием задачи относятся:
а) чтение задачи учеником;
б) восприятие задачи на слух (чтение задачи учителем или учащимся);
в) составление задачи по опоре (краткой записи, иллюстрации, инсценировке, схеме и т.д.);
г) трансформация задачи (из решенной задачи составляется новая) и т.д.
Для того чтобы решить задачу, ученик должен уметь выполнять следующую последовательность переходов:
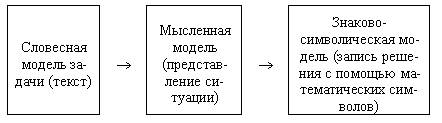
Каждая из моделей описывает единственный объект – задачу. Выполнены они на разных языках: языке слов, языке образов и языке математических символов. Для построения любой из этих моделей учащийся должен выделить только существенные свойства объектов и структуру связей и отношений между ними. Для математической модели – выделить количественные соотношения предложенной в задаче ситуации и связи между данными и искомым. Первый и второй пункты данной схемы относятся к этапу ознакомления с содержанием задачи.
На основе вышеперечисленного составляется «Памятка по решению задачи» (№ 1) для учеников начальных классов.
Памятка по решению задачи
1. Прочитай задачу, представь то, о чем говорится в задаче.
2. Запиши задачу кратко, если необходимо, сделай чертеж или схему.
3. Объясни, что показывает каждое число и назови вопрос задачи.
4. Подумай, какое число должно получиться в результате (например, больше или меньше, чем данные числа и т.д.)
5. Подумай, можно ли сразу ответить на вопрос задачи. Если нет, то почему? Что нужно узнать сначала? Что потом? Составь план решения задачи.
6. Выполни решение.
7. Проверь ответ и ответь на вопрос задачи.
8. Подумай, можно ли решить задачу другим способом?
9. Подумай, при каких условиях ответ задачи получился бы больше? Меньше?
Разумеется, можно варьировать последовательность вопросов в данной памятке в зависимости от конкретных условий, учитывать их взаимопроникновение.
Рассмотрим работу над следующей задачей «Из молока получается 10% творога. Сколько творога получится из 32,8 кг молока?» (задача для 5 класса).
Данная задача часто с трудом решается детьми, которые не представляют себе процесс производства творога. Поэтому после чтения условия задачи можно спросить детей, знают ли они, как делают творог, какие еще продукты получаются из молока при изготовлении творога (сыворотка). В данной ситуации не стоит жалеть времени на информацию о производстве творога, ведь это не только способствует решению данной конкретной задачи, но повышению общего уровня развития ребенка.
Далее следует поработать над фразой «Из молока получается 10% творога». Как вы это понимаете? Из какого количества молока получается 10% творога? (Из любого, т.е. из чайной ложки, 1 кг, 1 т и т.д.).
Масса полученного творога должна быть меньше или больше массы молока? (Меньше, т.к. творог получается из веществ, которые являются составной частью молока).
Краткую запись задачи можно сделать несколькими способами, желательно выбирать тот способ, который позволит облегчить поиск решения. Приведем примеры:
1)
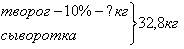
2) 10% от 32,8 кг – ?кг

3)
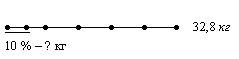
Кроме приведенных примеров, это могут быть и другие схемы, чертежи, рисунки, картинки и т.д. (все зависит от индивидуальных особенностей восприятия каждого ученика). Главное, чтобы при этом ребенок понял, о чем говорится в задаче.
Итак, что мы знаем из условия задачи? (У нас есть 32,8 кг молока, нужно найти, сколько творога получится из этого количества молока или, согласно условию задачи, 10% от 32,8 кг).
От какого числа следует найти 10 % в задаче? Как найти 10% от 32,8 кг? (32,8 кг разделить на 100% и результат умножить на 10).
Запишем решение
32,8:100×10=3,28 (кг).
Ответ: из 32,8 литра молока получится 3,28 кг творога.
Можно ли записать решение задачи по-другому? Как вы понимаете 10 % от чего-либо? (Десятая часть, десять сотых данного числа). Как найти 10 % или десятую часть от числа? (Разделить на 10; умножить на 0,1).
1 способ: 32,8:10=3,28 (кг);
2 способ: 32,8×0,1=3,28 (кг).
Если рассматривать термин «решение задачи» только как процесс нахождения ответа, то изменится только количество выделяемых этапов. В этом случае будем считать, что:
Решить задачу (в узком смысле) – не только дать ответ на вопрос задачи (назвать результат), но и объяснить, какие действия нужно выполнить над данными в ней числами, чтобы получить после вычислений искомое число или результат, либо доказать, что решения не существует, либо обозначить отношение, о котором спрашивается в задаче.
Записать решение задачи (если речь идет о конкретных числах) –при помощи цифр и знаков действий показать, что нужно сделать, чтобы найти неизвестное число, выполнить все эти действия и дать ответ на вопрос задачи.
С точки зрения данного подхода для решения задачи необходимо действовать по следующему плану:
а) раскрыть связи между данными и искомыми;
б) на основе этих связей выбрать действия для решения;
в) выполнить эти действия;
г) дать ответ на вопрос задачи.
Как видим, не проводится работа по проверке решения, последующая работа над задачей, однако, работа по чтению задачи, составлению плана решения подразумевается.
В данном случае используется следующая «Памятка по решению задачи» (№ 2):

Например, рассмотрим решение следующей задачи (на основе Памятки №2):
«За 5 метров ткани заплатили 30 гривень. Сколько стоит 1 метр этой ткани? (Какова цена ткани?)»
Прочитайте задачу. Повторите условие задачи. (За 5 метров ткани заплатили 30 гривень). Повторите вопрос задачи. (Сколько стоит 1 метр этой ткани?)
а) Если за 5 метров ткани уплатили 30 гривень, то за 1 метр нужно уплатить больше или меньше? (Меньше). Во сколько раз? (Нужно уплатить меньше в 5 раз).
б) Чтобы найти величину в 5 раз меньшую, чем 30 гривень, какое действие нужно выполнить? (Нужно 30 гривень уменьшить в 5 раз, значит, разделить на 5). Следовательно, задача решается действием деления.
в) Решение: 30:5 = 6 (грн.)
г) Ответ: цена ткани 6 гривень.
Работа по памятке №2 помогает детям полнее осознать понятие «задача», учит выделять ее составные части задачи и решение.
В дальнейшем, для работы над задачами целесообразно использовать конструктивную памятку, которая учит детей объяснять каждый шаг в решении задачи.

Проиллюстрируем работу по конструктивной памятке на конкретной задаче.
«На столе 5 карандашей, а в коробке на 2 больше. Сколько карандашей в коробке?»
Записи на доске и в тетрадях детей появляются в процессе работы по конструктивной памятке.
Известно. На столе 5 карандашей, а в коробке на 2 больше.
На доске появляется запись:
5 2
Спрашивается. Сколько карандашей в коробке (вместо вопроса ставится точка, т.к. эту запись в дальнейшем трансформируем в запись решения задачи).
5 2
Объясняю. Так как в коробке карандашей больше на 2, чем на столе, то буду выполнять сложение (в записи появляется знак «+»).
5 + 2
Решаю. К 5 карандашам прибавить 2 карандаша будет 7 карандашей (в записи появляется результат вычисления и наименование).
5 + 2 = 7 (кар.)
Ответ: 7 карандашей в коробке.
Работа над задачей, организованная таким образом позволяет ребенку использовать речевой образец, сначала вслух, а затем про себя.
Упражнения
1. «Масса сушеных яблок составляет 16% массы свежих яблок. Сколько надо взять свежих яблок, чтобы получить 4 тонны сушеных? Сколько сушеных яблок получится из 4,5 тонн свежих яблок?»
Проанализируйте задачу, решите ее в соответствии с памяткой №1, конструктивной памяткой. Подумайте, какие трудности могут возникнуть во время работы над содержанием задачи. Предложите различные формы краткой записи. Какой вам кажется наиболее удобным? Почему?
2. Дана задача: «Утром на элеваторе было 96 т пшеницы. К полудню привезли еще пшеницу на трех машинах по 3 т на каждой. Сколько тонн пшеницы осталось на элеваторе, когда 3/5 всей пшеницы отправили на мельницу?»
Рассмотрите различные способы иллюстрации этой задачи.
а)
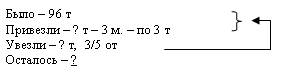
б)
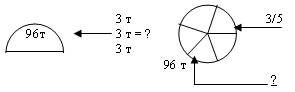
в)
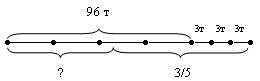
Какой из данных способов иллюстрации кажется вам более удачным? Почему? Какой способ предложили бы вы? От чего зависит выбор способа иллюстрации задачи?
3. Дана задача: «Вертолет за 2 часа пролетел 480 км. Сколько километров пролетит за 5 часов самолет, если его скорость в 3 раза больше скорости вертолета?» Проиллюстрируйте эту задачу различными способами. Нарисуйте словесную картину того, что происходит в задаче. Разбейте текст задачи на смысловые ситуации. Надо ли учителю иллюстрировать задачу по-разному?
Понятие задач одного вида
Л.М. Фридман, Е.Н. Турецкий в школьном курсе математики выделяют следующие виды задач, отвечающие таким признакам:
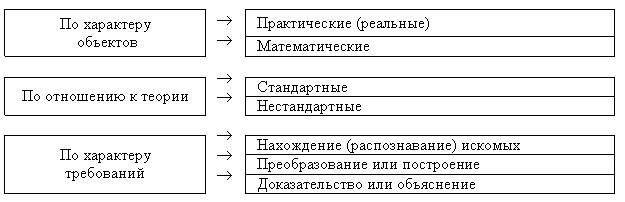
Классификация простых и составных задач, решаемых в начальной школе, производится по признаку отношения к теории, т.е. задачи подразделяются на стандартные и нестандартные. Некоторые методисты называют эти задачи соответственно алгоритмическими и эвристическими. При этом стоит отметить, что данное деление является условным, в связи с тем, что любая из задач может содержать как стандартный, так и нестандартный (творческий) компонент.
Математические задачи, для решения которых в школьном курсе математики имеются готовые правила (в виде словесного алгоритма, формулы, тождества и т.д.) или эти правила непосредственно следуют из правил, теорем, определений программного минимума называют стандартными. При этом предполагается, что для решения этих задач имеются вполне определенные правила-алгоритмы (отсюда – алгоритмические).
Начальный курс математики содержит в себе несколько основных групп задач, решение которых основывается на одних и тех же связях между данными и искомым, а отличаются лишь конкретными числовыми данными и сюжетом (стандартные). Именно эти группы задач методисты начальной школы называют задачами одного вида.
Вообще задачи, связанные между собой таким образом, можно называть стандартными, задачами одного вида (видовыми) или задачами одного типа (типовыми). Однако, часто термин «тип» используется как собирательный для нескольких видов задач.
Например, задачи на четвертое пропорциональное (тип) подразделяются на 6 видов (Бантова М.А., Бельтюкова В.Г.), которые в других источниках называют видом и подвидами, поэтому имеет смысл внимательно просматривать сам первоисточник, чтобы определиться со смыслом используемой терминологии.
Приведем пример задач одного вида.
1. В одной коробке 6 карандашей, во второй – в 3 раза больше. Сколько карандашей в двух коробках вместе?
2. В первом аквариуме 8 рыбок, а во втором – в 2 раза больше. Сколько рыбок в двух аквариумах?
Данные задачи отличаются сюжетом: в первой речь идет о карандашах в коробках, а во второй – о рыбках в аквариумах. Числовые данные в данной ситуации тоже различны, однако обе задачи имеют одинаковую теоретическую основу – увеличение в несколько раз и нахождение численности объединения двух непересекающихся множеств. По способу решения они имеют один алгоритм – сначала требуется найти, сколько предметов во втором случае, а потом – сколько вместе. Поэтому их можно назвать задачами одного вида.
Упражнения
1. Какие задачи называют стандартными? Приведите примеры стандартных задач.
Схема

Для решения задач подразумевается выполнение следующего плана, который является общим для решения задач любого вида и любого способа решения, все выделенные этапы представляют собой норму деятельности человека по решению задач.
Однако в реальном процессе решения не обязательно проходить через все перечисленные этапы. Это зависит от того, насколько решающему известен способ решения задачи. Поэтому в начальной школе можно использовать следующий план работы над задачей.
План полной работы над задачей
1. Изучение текста задачи и его анализ.
2. Выделение связей между данными и искомыми.
3. Поиск способа решения и составление плана решения.
4. Осуществление плана решения. Ответ на вопрос задачи.
5. Проверка решения задачи.
6. Анализ решения и полученных результатов.
7. Творческая работа над задачей.
Поиск способа решения
Выделяются две разновидности поиска способа решения задач:
1. явный – непосредственно разбор задачи;
2. неявный – анализ содержания задачи, работа с иллюстрацией задачи и т.д.
Итак, как же искать план решения задачи? Профессор математики С.А. Яновская сказала, что «решить задачу – это свести её к уже решенным». Другими словами, разбить каждую задачу на систему подзадач, которые уже умеем решать. Проблема в том, каким образом выделить эти подзадачи, как их увидеть? Как воспользоваться советом С.А. Яновской?
Определенных правил для такого сведения незнакомых задач к знакомым не существует, но если внимательно, вдумчиво проанализировать задачу, вдумчиво решать каждую задачу, фиксируя в памяти способы её решения, есть возможность научиться решению любых задач.
В начальной школе при знакомстве с задачами нового вида чаще всего учитель знакомит детей со способом решения задачи, но, для того, чтобы это не выглядело просто списыванием с доски готового решения, учитель при помощи специально организованной системы вопросов проводит так называемый разбор задачи.
Способ 2
Расположим схему таким образом:

Из схемы видно, если убрать из каждого набора по шишке и желудю, то останется шишка и желудь. Теперь перейдем к массам этих объектов. Если от массы двух шишек и желудя отнять массу двух желудей и шишки, то полученный результат покажет разность масс шишки и желудя. Таким образом, ответ на вопрос «На сколько тяжелее?» будет получен. Что тяжелее – шишка или желудь видно из рисунка. Выполним вычисления:
1) 152 – 94 = 58 (г).
Далее, если мы к массе двух шишек и одного желудя добавим полученную разность, то мы получим массу трех шишек:
2) 152 + 58 = 210 (г).
Отсюда масса шишки
3) 210:3 = 70 (г),
а масса желудя
4) 70 – 58 = 12 (г).
Ответ: масса желудя 12 г, масса шишки 70 г. Шишка тяжелее желудя на 58 г.
Способ 3
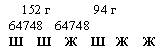
Из схемы видно, что у нас всего 3 шишки и 3 желудя (это можно определить пересчитыванием, либо оформить двумя арифметическими действиями), общая масса которых составляет
1) 152 + 94 = 246 (г).
Масса пары (желудь–шишка) составляет
2) 246:3 = 82 (г).
Можно составить еще одну схему (по необходимости)

из которой видно, что масса одной шишки может быть получена следующим образом:
3) 152 – 82 = 70 (г).
Далее находим массу желудя:
4) 82 – 70 = 12 (г).
5) 70 – 12 = 58 (г)
Ответ: масса желудя 12 г, масса шишки 70 г. Шишка тяжелее желудя на 58 г.
Обучение детей схематизации задач и составлению краткой записи представляет собой целенаправленный достаточно длительный процесс. Схематизация каждой из задач не является однозначной, составление схемы – процесс индивидуальный. Однако обучение использованию различных вариантов схематической записи задачи иногда позволяет ребенку увидеть разные способы решения задачи
Интересную методику обучения схематизации задач при помощи приема противопоставления различных форм наглядной интерпретации задач, предлагает Н.Б. Истомина (в учебниках математики Н.Б. Истоминой).
Использование элементов данной методики при работе по традиционным программам позволит усовершенствовать умения и навыки учеников по решению задач.
В процессе этой работы у учащихся должно быть выработано умение чертить отрезки, складывать и вычитать отрезки; умение описывать предметные и текстовые ситуации, схематизировать и математизировать их.
Два ученика Маша и Миша иллюстрируют тексты задач, при этом каждые по-разному. В одном из ответов содержится типичная ошибка, допускаемая детьми. При этом, на наш взгляд, можно показывать одновременно и несколько правильных интерпретаций.
Необходимо проводить работу, направленную на понимание соотношения целого и его частей. Со старшими дошкольниками по формированию элементарных математических представлений такая работа проводилась. С первоклассниками ее можно организовать на примерах отрезков.
Например:
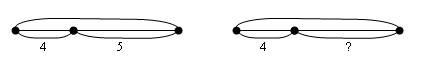
«Посмотри на схему. Что будешь искать: целое или часть?»
После введения понятия буквенного выражения можно использовать схемы с буквами. Также можно использовать и такие упражнения: «В корзине 15 грибов. Из них 5 белых, а остальные лисички. Обозначь все грибы кругами и покажи, сколько в корзине лисичек» (СНОСКА: Истомина Н.Б., Нефедова И.Б. Первые шаги формирования умения решать задачи // Начальная школа. – 1998. - №11-12. - С.42-48)
Маша выполнила задание так:

А Миша так:

Кто выполнил задание верно?
Однако, к помощи Миши и Маши авторами приема рекомендуется прибегать только тогда, когда учащиеся сами не могут справиться с заданием.
Рассмотрим составную задачу: «В вазе 15 конфет. Из них 4 шоколадных, 5 ирисок, а остальные – леденцы. Сколько леденцов в вазе?»
Стандартная модель (краткая запись) выглядит так:
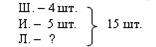
От исходной модели можно перейти непосредственно к схемам решения:

Или
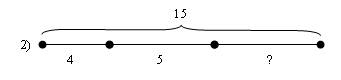
На наш взгляд, последняя схема позволит быстро найти путь к решению задачи.
Многоступенчатость составления краткой записи позволяет ребенку рассмотреть задачу со всех «сторон», позволяет найти различные способы решения задач.
Также можно обучать учеников составлению графов-моделей (схем) задачи (СНОСКА: Подробнее: Белошистая А.В. Прием графического моделирования при обучении решению задач. // Начальная школа. – 1991. - № 4. – С.18 -24), начиная с решения простых задач на нахождение суммы и остатка.
Идея построения граф-схемы задачи основывается на том, что в условии задачи рассматриваются связанные зависимостью элементы. Эти зависимости выражаются отношениями, которые обычно связывают три величины. Такие связанные тройки величин представляют собой либо простую задачу, либо простые задачи, входящие в составную задачу. Они и являются основными компонентами структуры задачи. Схематично каждая из связок представляется в виде своеобразного «треугольника». Структура составной задачи на схеме обычно выглядит как объединение конечного числа таких «треугольников».
Например, рассмотрим задачи «В коробке было 5 карандашей. Миша положил туда еще 2 карандаша. Сколько карандашей стало?» и «В коробке лежало 5 карандашей. 2 карандаша взяли. Сколько карандашей осталось в коробке?».
Разбор задач на нахождение суммы и остатка проведем от данных к вопросу и от вопроса к данным, при этом, обучая детей составлять схемы разбора и решения задачи. В схемах можно использовать также и знаки арифметических действий, что позволяет трансформировать их в план-схему решения задачи.
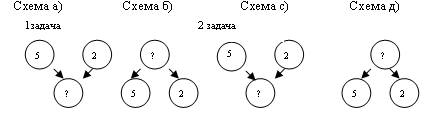
Схемы (а) и (с), а также (б) и (д) совпадают. Практически по каждой из схем можно составить два числовых выражения со знаком (+) и (–). Поэтому детям можно предложить добавить в схемы знаки арифметических действий, чтобы схема относилась к конкретной задаче.
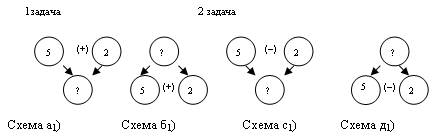
При обучении детей составлению граф-схем необходимо помнить, что схема составляется не после того, как задача прочитана детьми и проанализирована, а во время чтения текста и анализа условия. Таким образом, сначала появляется схема типа (а) – (д), а затем они трансформируются в схемы (а1) – (д1).
Упражнения
1. Пронаблюдайте в учебниках [Б1], [Б2], [Б3] как вводятся различные виды краткой записи задач, граф-схемы разбора задач.
2. Составьте и решите такую составную задачу, чтобы она содержала в себе следующие две простые задачи: а) увеличение числа в несколько раз; б) нахождение суммы.
3. Даны задачи: «Масса дыни 1 кг 200 г. Ваня съел 1/6 дыни, а Маша – 1/5 дыни. На сколько граммов дыни больше съела Маша?» и «У Андрея 123 марки, это в 3 раза больше, чем у Алеши. На сколько марок у Алеши меньше, чем у Андрея?» Запишите задачи кратко, решите по действиям. Сделайте схемы разбора задач. Выделите на схеме простые задачи. Определите их вид.
4. Составьте схему для решения задачи и решите ее арифметически: «Для изготовления стекла для бутылок берут 25 частей кварцевого песка, 9 частей соды, а извести на 4 части меньше, чем соды. Сколько надо взять песка, если извести и соды взяли 700 ц?»
Схема
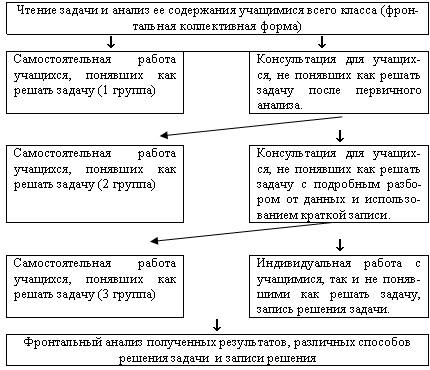
На основе приведенной схемы можно работать над задачами нового или уже изученного вида. Рассмотрим различные варианты применения многоступенчатости в работе над задачами.
Дифференцированная работа над задачами нового вида
Проанализируем особенности восприятия задач нового вида учащимися разных типологических групп, которая составлена нами на основе данных В.А. Крутецкого.
| Способные к математике учащиеся | Воспринимают задачи аналитически (расчленяют задачу на структурные элементы, оценивают, систематизируют их) и синтетически (перегруппировывают структурные элементы, выделяют отношения и зависимости). Каждую состоящую из структурных элементов структурную единицу воспринимают целостно, в комплексе, не умаляя роли каждого элемента в этой структуре. У способного ученика создается четкий целостно-расчлененный образ задачи. |
| Учащиеся со средними способностями | При восприятии задачи нового типа воспринимают, как правило, ее отдельные математические элементы. Часто, переключаясь от одного элемента задачи к другому, теряют предыдущий элемент. Среднему ученику необходимо ставить специальную задачу на связывание математических элементов задачи, в процессе анализа и синтеза он находит эту связь. |
| Неспособные к математике учащиеся | Связи и соотношения между элементами задачи, даже с посторонней помощью, устанавливаются у них с большим трудом. Им очень трудно дается осмысление связей между компонентами задачи, они с трудом охватывают совокупность зависимостей в задаче, не отличают существенных признаков от несущественных. Слабым учащимся бывает трудно отвлечься от конкретного содержания задачи, за сюжетом задачи эти дети не видят ее подлинного математического смысла. |
Из данных таблицы видно, что, средние ученики воспринимают в задаче нового типа (а неспособные — вообще во всех задачах) на первых порах лишь разрозненные данные, что они поначалу «прикованы» к конкретным данным. Исходя из этого, должна быть организована дифференцированная работа над задачами нового вида.
Кроме схемы многоступенчатого объяснения материала, для организации дифференцированной работы над задачами с учетом особенностей типологических групп учащихся, можно предложить следующую схему работы над введением задач нового вида (разработана на основе схемы Хмуры А.А.):
Схема
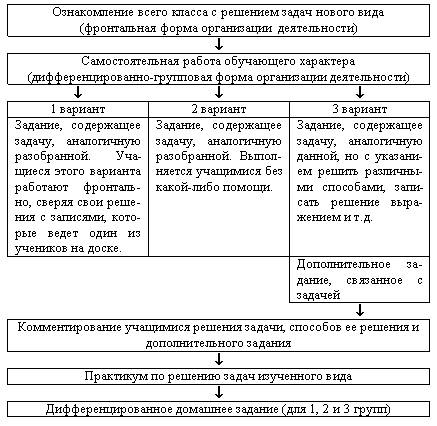
При такой организации работы над задачей нового вида сразу после объяснения учителя (раскрытие основных связей задачи, предъявление образца решения) проводится самостоятельная работа обучающего характера, которая позволяет выявить, на сколько усвоен материал с первого раза.
Организовать самостоятельную работу можно по-разному. В соответствии со схемой, можно использовать задания трех уровней сложности, которые отличаются не количеством работы, подлежащей выполнению, а ее качественными показателями, уровнем помощи. Например, задания первого варианта – алгоритмического, репродуктивного характера с элементами помощи, второй вариант требует переноса знаний, третий вариант предусматривает элементы творческого применения знаний. Каждый учащийся может самостоятельно выбрать посильный ему вариант. Важно подобрать задания таким образом, чтобы каждый учащийся работал над заданием с максимальной отдачей.
Во время выполнения заданий учениками учитель имеет возможность организовать индивидуальную помощь нуждающимся в ней. Сильные учащиеся, после выполнения основной части задания и проверки, переходят к выполнению дополнительного задания. Когда основная часть учащихся закончила работу над заданием, сильные учащиеся комментируют решение своего задания. Практикум по решению задач может быть организован в виде работы в гетерогенных группах (группы учащихся разных типологических групп), где более сильные учащиеся работают консультантами для слабых учащихся.
Дифференцированное домашнее задание имеет смысл подобрать так, чтобы оно стало логическим продолжением классной самостоятельной работы. Например, можно предложить учащимся решить задачи следующего варианта классной работы, а тем, кто выполнял задания третьего уровня, подобрать специальное задание.
Дифференцированная работа на этапе закрепления навыков решения задач данного вида
Рассмотрим схему организации учебно-познавательной деятельности учащихся, которая составлена на основе схемы Т. Горы и С.А. Логачевской (СНОСКА: Подробнее см. Гора Т., Логачевська С. Диференційований підхід до розв’язування текстових задач // Початкова школа. – 1998. – №1. – С.17-22).
Схема
| 1 вариант | 2 вариант | |
| І этап | Коллективный анализ условия и требования задачи, составление плана, схематическая запись решения на планшетах | |
| ІІ этап | Самостоятельная запись решения задачи в тетрадях. | Коллективный анализ подобной задачи с упрощенными числовыми данными. Запись решения с комментированием. |
| ІІІ этап | Самостоятельное решение подобной задачи с усложненными числовыми данными. | Коллективный анализ подобной задачи с измененным сюжетом. |
| ІV этап | Творческое задание. | Самостоятельное решение подобной задачи с измененными числовыми данными и сюжетом. |
Во время коллективного анализа текста задачи устно составляется план ее решения, затем учащиеся записывают схематически решение на специальных планшетах-черновиках и показывают решение учителю, который обходит класс. Если задача решена правильно, дети выполняют задание первого варианта, если с ошибкой – работают под руководством учителя над заданиями второго варианта. Часто учащиеся после первого самостоятельного чтения уже знают, как решать задачу, поэтому усложняющиеся задания для самостоятельного выполнения сообщаются учащимся сразу. Задания второго варианта предъявляются учителем с постепенным переходом к самостоятельному выполнению.
Рассмотри возможные варианты организации такой работы.
Задача 1: «В магазин привезли 18 ящиков винограда по 6 кг в каждом и 21 ящик персиков по 9 кг в каждом. Сколько килограммов фруктов привезли в магазин?»
І этап.
Прочитайте задачу. Составьте план решения.
План: 1) найти, сколько килограммов винограда привезли; 2) найти, сколько килограммов персиков привезли; 3) найти, сколько всего фруктов привезли в магазин.
ІІ этап.
1вариант. Самостоятельно запишите решение задачи (форму записи оговорить, например, по действиям с пояснениями или выражением).
2 вариант. Фронтальная работа. По заранее заготовленной краткой записи задачи с аналогичным сюжетом, но облегченными числовыми данными проводится анализ задачи, составляется план решения. Затем решение записывается с комментированием.

Решение обеих задач (1 и 2 варианты) проверяется коллективно. Таким образом, решение исходной задачи оказывается разобранным и ученики 2-го варианта тоже его видят, при этом они выполняют решение аналогичной типовой задачи и имеют возможность провести сравнение решений.
ІІІ этап.
1 вариант. Самостоятельно реши задачу (предлагается аналогичная задача с измененными числовыми данными и сюжетом).
Задача 2: «Дети купили 5 пакетов молока по 1 грн. 80 коп за пакет и 4 упаковки творожного десерта по 3 грн. 30 коп за упаковку. Сколько они заплатили за покупку?»
2 вариант. Фронтальная работа.
Задача 3: «Для оформления утренника детям привезли фломастеры в пачках. 6 пачек по 6 фломастеров в каждой и 3 пачки по 12 фломастеров в каждой. Сколько всего фломастеров привезли?»
Фронтальная проверка заданий двух вариантов.
IV этап.
1 вариант. Составь задачу по схеме (можно указать направление, например, «Магазин», «Почта», «Строительство» и т.д.) и вопросу

Например: Сколько денег уплатили? Сколько открыток купили? Сколько квартир построили?
2 вариант. Самостоятельно реши задачу (предлагается задача с измененным сюжетом и числовыми данными).
Задача 4: «Дети собрали 8 корзинок по 10 рыжиков в каждой и 5 корзинок по 14 груздей в каждой. Сколько всего грибов собрали дети?»
Задания анализируются фронтально.
Упражнения
Рассмотрите дифференцированные задания для работы над задачами разных видов в статье: Гора Т., Логачевська С. Диференційований підхід до розв’язування текстових задач // Початкова школа.–1998.–№1.–С.17-22. Составьте аналогичные упражнения для каждого вида задач. Что, на ваш взгляд, можно добавить к этим упражнениям. Предложите свои варианты заданий.
Приемы дифференцированной помощи при самостоятельной работе над текстовой задачей
При организации самостоятельной работы учащихся над задачами М.В. Богданович выделяет следующие три вида дифференциации:
1. индивидуализация требований к общему заданию:
§ постановка нескольких вопросов к одному условию, каждый отвечает на столько вопросов, на сколько ему по силам;
§ варьирование требований к решению задачи;
§ задание с тремя задачами, в котором задачи похожи, но имеют разную степень сложности, решение начинается со второй задачи, тот, кто с ней справляется – решает третью, кто не справляется – переходит к первой;
§ дополнительное задание, несвязанное с основным и т.д.;
2. упрощение одного из вариантов самостоятельной работы (ранее решенная задача, смена числовых данных);
3. оказание индивидуальной помощи при решении задач одного из вариантов:
§ конкретизация задачи с помощью карточки с иллюстрацией к задаче или краткой записью;
§ сообщение ответа задачи до ее решения;
§ сообщение плана решения, схемы решения, начала решения, постановка наводящих вопросов и т.д. [3].
В процессе самостоятельного решения задач на уроке учитель должен также учитывать индивидуальные особенности детей, качество сформированности их учебно-познавательной деятельности, конкретный, сиюминутный уровень умений решать задачи данного вида.
Выделяются следующие этапы работы учащихся над решением задачи: мотивационный; ориентировочный (анализ текста, выделение связей и зависимостей, моделирование, планирование решения); исполнительский (выполнение плана решения); контрольно-оценочный (проверка решения).
Часто контрольно-оценочный этап в решении задач ученики пропускают, а учителя не уделяют достаточного внимания формированию навыков самоконтроля ученика. Рассмотрим возможные варианты дифференцированного подхода к организации помощи в решении и одновременной проверки решения задачи.
1. Представление учащимся образца решения. Образец может быть записан на доске и закрыт до необходимого момента. Также образец можно записать на индивидуальной карточке и раздать нуждающимся в нем учащимся.
2. Использование вспомогательных карточек-схем решения каждой конкретной задачи. Этот способ является одновременно и способом дифференцированной помощи и способом формирования самоконтроля у учащихся в процессе решения задач.
3. Использование карточек с планом решения задачи.
4. Использование сигнальных карточек, содержащих основные теоретические факты для решения задачи.
5. Использование карточек с двумя вариантами решения задачи – верным и неверным, который предусматривает типичные для данного учащегося ошибки.
Проиллюстрируем возможные способы дифференцированной помощи. Например, учащимся дана следующая задача: «Пешеход за 4 часа прошел 16 км. Какое расстояние он пройдет за 5 часов?» Карточки дифференцированной помощи можно предложить такие:
1. Образец решения:
1) 16:4 =4 (км/ч) – скорость пешехода;
2) 4·5=20 (км) – пройдет за 5 часов.
2. Карточка-схема:
а) без числовых данных
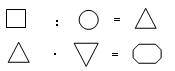
б) с частью числовых данных
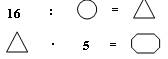
Схемы решения помогают учащемуся спланировать свои действия, выбрать нужное арифметическое действие в случае такой необходимости.
3. Карточка с планом решения:
1) Найди скорость пешехода.
2) Найди расстояние, которое пешеход пройдет за 5 часов.
4. Карточка с формулами:
Выбери нужные формулы для решения и примени их:
s = v·t
v = s:t
t = s:t
5. Карточка с верным и неверным решением:
Выбери правильное решение:
(16:4)·5
(5·4)·16
Детям, которые справились с решением задачи необходимо предложить дополнительное задание, работа над которым прерывается сразу, как только остальные решают основную задачу.
Дифференцированная работа над задачей при проверке домашнего задания
Домашние задания, как справедливо отмечает А.Я. Савченко, тоже необходимо дифференцировать. Дифференциацию можно осуществлять по объему задания и его сложности.
Задание может быть как одинаковым по содержанию, так и различным. Например: некоторые учащиеся вообще не получают домашнего задания; некоторым учащимся предлагают решить только задачи определенного вида; задачи «на выбор» – одну из двух – трех; самим выбрать задачи для домашней работы и т.д.
Все зависит от конкретной цели урока, цели домашнего задания, особенностей детей. Если на уроке дети познакомились с решением задач нового вида, то домашнее задание может быть одинакового содержания, но слабым учащимся можно задать просто решить задачу, а сильным – после решения домашней задачи провести творческую работу над ней. Можно предложить: решить задачу всеми возможными способами; изменить данные так, чтобы задача решалась по-другому; составить аналогичную задачу, записать ее условие на карточке, решить ее. Карточку с условием составленной учеником задачи (после соответствующей проверки учителем) можно использовать для проверки выполнения домашнего задания другими учениками на следующем уроке.
Если домашнее задание не содержит задач нового вида, то можно предложить учащимся вариативное домашнее задание из двух частей: первая часть задания репродуктивного характера, а вторая – частично-поискового или творческого. Выполнить задание детям предлагается «на выбор».
В процессе проверки домашней задачи работа может проводиться в следующей форме: сверка решения с образцом; взаимопроверка, если задача решается только одним способом, пояснения числовых выражений, из которых состоит решение; решение подобной задачи; составление и решение обратных задач.
Для группы слабых учащихся, которые, может быть, не решили домашнюю задачу (если их незначительное количество) можно организовать дополнительные занятия. В случае, когда с задачей не справились многие, необходимо организовать фронтальную работу, а учащимся, справившимся с заданием предложить дополнительные задания. Также для сильных учащихся можно приготовить карточки, которые предусматривают творческую работу над решенной дома задачей.
Упражнения
1. Во время контроля учащимся была дана задача: «Двое рабочих, работая одинаковое число дней, изготовили 5160 деталей. Один из них изготовлял в день 212 деталей, другой 218 деталей. Сколько деталей за это время изготовил каждый рабочий?» Некоторые дети справились с этой задачей раньше и получили от учителя карточки с такими заданиями: «а) измени эту задачу так, чтобы в ней появилось еще одно действие; б) измени одно из чисел в задаче так, чтобы ответ уменьшился в 2 раза». Как вы думаете, почему учитель дал такие карточки, а не просто новое задание? Составьте по этой задаче еще 3 карточки с той же целью.
2. На дом была задана задача: «В магазин привезли на машине 130 кг апельсинов. Когда выгрузили несколько ящиков апельсинов по 5 кг каждый, то на машине еще осталось 60 кг. Сколько ящиков апельсинов выгрузили?» Спланируйте проверку домашней задачи в форме устного счета, состоящего из задач. Постарайтесь сделать это так, чтобы было интересно и тем детям, которые решили задачу правильно. Каковы преимущества такого способа проверки домашнего задания?
Вопросы и указания для самостоятельной работы
(СНОСКА: Составлено совместно с Виноградовой Т.Н. и Бажан З.И)
1. Дайте (если это возможно), определение текстовой задачи. Какие составные части ее содержания вы знаете? Особенности содержания некоторых задач. Как неформально отделить условие от требования? Как разбить задачу на смысловые ситуации? [15] п. 17, № 1–4.
2. Какие приемы ознакомления с содержанием задачи вы знаете?
Какие приемы считаются «активными» и почему?
1) ознакомление по тексту:
§ рассказывает учитель;
§ читает учитель;
§ читает ученик;
§ читают все дети.
2) дети сами составляют задачу:
§ по зрительной опоре;
§ по словесным указаниям;
§ переделывая из знакомой задачи.
Предложите еще приемы ознакомления, если они есть.
[1] с. 236–237, 284; [6] с.94; [3] с. 22–24.
3. Анализ содержания задачи и его значение. Приемы анализа содержания, их раздельное и комплексное применение. [15] п.19 №1,2.
4. Способы иллюстрации содержания задачи. Их роль и место в анализе содержания задачи. Как их применение может быть связано с типом математических способностей ребенка? Как учитель может учесть эти связи в своей работе? [3] с.29–31; [9] с.334–362.
5. Поиск решения задачи (разбор), его определение. Схема разбора задачи. Виды разбора и их отражение на схеме разбора. Неразрывность анализа и синтеза в мышлении. Виды разбора:
а) от вопроса (аналитический);
б) от данных (синтетический);
в) комбинированный.
Критерии выбора способа разбора данной задачи.
[15] с.56 №4, с.57 № 5; [3] с.134-136, с.25-29.
6. Способы решения текстовой задачи:
а) арифметический;
б) алгебраический;
в) графический;
г) практический;
д) подбором;
е) в виде схематической модели.
Применимость данных способов в начальных классах. Отличие способа решения от способа записи решения. [15] n.18 №1,2,3,4; [6] с.92–112.
7. Для каждого способа решения укажите возможные способы записи решения и оцените их применимость в начальной школе. [15] с.55–56 №2, с.57 № 6; [3] с.21–43; [1] с.191–192; [4] с.177–179.
8. Последующая работа над решенной задачей. Ее цели:
а) проверка правильности решения (рассмотрите способы проверки решения и условия их применимости);
б) формирование умения решать задачи данного вида;
в) подготовка к изучению нового материала с использованием данной задачи.
Изучите виды последующей работы над задачей и попробуйте их использовать, учитывая их особую ценность при формировании умения решать задачи.
[15] n.21 № 1,2; [1] с.192–204; [3] с.43-48, гл.II, §3.
9. Подготовительная работа к задаче. Ее связь со схемой разбора задачи. Роль подготовительной работы в анализе задачи. Рассмотрите фрагменты подготовительной работы к задаче в методической литературе и попробуйте планировать такую работу в своих уроках. [1] с.27, с.223–224, с.231–233.
10. Формирование умения решать текстовые задачи.
Цели, которые обычно ставятся:
а) ученик должен уметь самостоятельно решить любую задачу, входящую в программный минимум;
б) ученик должен уметь правильно записать решение в соответствии с требованиями;
в) ученик должен уметь объяснить решение.
Методы и приемы, применяемые для обучения детей решению задач и цели, которые достигаются при этом:
а) алгоритмизация процесса работы над задачей; памятка и методика работы с ней, сроки такой работы и достигаемые цели;
б) последующая и творческая работа над задачей, ее возможные формы и условия применения, цели;
в) приемы, сводящиеся к тому, что ученик исполняет роль учителя, давшего образец работы (метод В.Ф. Шаталова, метод С.Н. Лысенковой), метод обучения актеров в китайском театре; правила применения и достигаемые цели;
г) метод противопоставления и сравнения задач, методика УДЕ, ее основы, применение и достигаемые цели.
[1] с.192–204, с.227–229; [6] с.93–94; [3] гл. II §3; [18] с.28, §§ 24,25
11. Сколько текстовых задач целесообразно решить на уроке? Сколько возможно решить? Роль текстовых задач в обучении.
Приемы насыщения урока текстовыми задачами:
а) специальные пособия для насыщения урока задачами;
б) цепочки и каскады задач;
в) преобразование и деформация задач с последующим их решением;
г) применение методики УДЕ.
Каждый из примеров использует особенности человеческого мышления, его резервы. Какие? Изучите эти приемы и их основу, многообразие достигаемых при их применении целей. Попробуйте их применить на уроках. [7] с.48–56; [3] с.62–68, с.48–50; [18] с.28 §§24,25.
12. Умение решать задачи формируется у разных детей по-разному и в различные сроки. От чего это зависит? Именно с этим связан тот факт, что работу по обучению детей решению задач надо вести дифференцированно. Что такое дифференцированная работа над задачей, и каковы ее формы? Дифференцированная устная фронтальная работа над задачей; дифференцированная работа с памяткой на уроках; приемы дифференцированной помощи при самостоятельной работе над текстовой задачей; дифференцированная работа над задачей при проверке домашнего задания; дифференцированная дополнительная работа над задачами. [3] с.10–22, с.87–94; [7] с.49,57; [1] с.227–229.
13. Что такое задачи программного минимума? Рассмотрите их классификацию и найдите их место в учебниках математики, которые вы используете в работе. [3] с.10–22.
14. Задачи, не входящие в программный минимум, задачи с логической нагрузкой или усложненные в начальном курсе. Изучите их классификацию, найдите их в учебниках, решите. Какие роли отведены им в процессе обучения детей решению задач? [3] c.118–126.
Вопросы для самоконтроля
1. Что называется текстовой арифметической задачей?
2. Из каких частей состоит текстовая арифметическая задача?
3. Что значит решить задачу?
4. Что такое простая задача?
5. Что такое составная задача?
6. Какова роль решения задач в начальной школе?
7. Что значит научить детей решать задачи?
8. Из каких этапов состоит методика работы над задачей?
9. Какая подготовительная работа должна проводиться перед решением задач?
10. Расскажите о работе по ознакомлению с решением задач:
а) перечислите этапы этой ступени;
б) раскройте смысл термина «ознакомление с решением задачи».
11. Расскажите об этапе поиска решения задачи (краткая запись, схема, чертеж, предметная иллюстрация, разбор задачи, его целесообразность, кем проводится, чем заканчивается).
12. Способы разбора составной задачи (от вопроса к данным, от данных к вопросу, комбинированный). Раскройте на конкретных примерах.
13. Основные формы записи решения задач, используемые в начальной школе. Расскажите о них. Приведите примеры.
14. Проверка решения задачи. Перечислите способы проверки, приведите примеры.
15. Расскажите об этапе закрепления решения задач данного вида, его составных частях.
16. Расскажите о роли упражнений творческого характера и задач повышенной трудности.
17. Задачи с недостающими и избыточными данными. Их роль в обучении младших школьников решению задач. Приведите примеры. Трансформируйте задачи так, чтобы появилась возможность решить как можно больше задач.
18. Расскажите о роли составления новых задач и преобразования задач для обобщения знаний учащихся.
19. Проиллюстрируйте каждое из предложенных типов заданий:
§ Постановка требования к данному условию задачи или изменение требования.
§ Составление условия задачи по данному требованию.
§ Подбор числовых данных к задаче и их изменение.
§ Составление задач по аналогии.
§ Составление обратных задач.
§ Составление задач по иллюстрации, краткой записи, схеме.
§ Составление задачи по данному решению.
§ Преобразование данных задач в задачи родственных видов.
Тестовые задания
Проверьте свои знания
Выбрать правильный ответ.
1. Простая задача – это:
а) легкая задача;
б) задача, в содержании которой есть только один вопрос;
в) задача, которая решается в одно арифметическое действие.
2. Какова особенность формулировки содержания задачи (из предложенных выбрать полный ответ): «50 кг краски упаковали в 10 банок. Сколько потребуется банок для упаковки 35 кг краски?»
а) требование задачи сформулировано в вопросительной форме;
б) требование задачи сформулировано в вопросительной форме и содержит в себе часть условия задачи;
в) в задаче недостаточно данных для выполнения требования (не сказано как упаковывали краску в банки – поровну или нет) и часть условия включена в одно предложение с требованием, которое сформулировано в вопросительной форме.
3. Расположить последовательно следующие этапы работы над задачей:
а) запись решения задачи;
б) последующая работа над задачей;
в) работа над содержанием задачи;
г) запись ответа на вопрос задачи;
д) поиск решения задачи.
4. Этап работы над содержанием задачи включает в себя:
а) краткую запись задачи;
б) запись решения задачи;
в) чтение текста задачи и словарную работу;
г) составление плана решения задачи;
д) выделение данных и искомых;
е) пересказ текста задачи;
ж) переформулировка задачи.
5. Если задача решена арифметическим способом, то решить задачу другим способом – это:
а) решить задачу арифметическим способом, отличным от первого;
б) записать решение задачи выражением;
в) выполнить чертеж или составить рисунок, который позволит легко дать ответ на вопрос задачи;
г) решить задачу составлением уравнения;
д) использовать счетный или другой материал, позволяющий практически ответить на вопрос задачи.
6. Составная задача – это:
а) задача, которая состоит из нескольких простых задач, связанных между собой;
б) сложная, трудная задача;
в) задача, которая решается в два или более арифметических действий.
7. Какова особенность формулировки содержания задачи (из предложенных вариантов ответов выбрать полный): «Сколько дверей нужно покрасить мастеру в двух квартирах, если в одной квартире 6 дверей, в другой – 4 двери, и мастер покрасил уже 7 дверей?»
а) требование задачи содержит в себе все условие задачи и сформулировано в вопросительной форме;
б) задача с избыточной информацией (мастер уже покрасил 7 дверей), которая не нужна для выполнения требования задачи, и требование задачи содержит в себе все условие задачи и сформулировано в вопросительной форме;
в) требование задачи сформулировано в вопросительной форме.
8. Этап «Поиск решения задачи» включает в себя:
а) оформление краткой записи задачи;
б) разбор задачи от данных к вопросу (синтез);
в) составление плана решения задачи;
г) комбинированный разбор задачи;
д) решение задачи другим способом;
е) разбор задачи от вопроса к данным.
9. Формы проверки решения задачи:
а) решение задачи другим способом;
б) разбор задачи другим способом;
в) прикидка;
г) соотнесение полученного результата и условия задачи;
д) составление и решение обратной задачи;
е) составление аналогичной задачи с последующим решением.
Список использованной литературы
Основная литература
1. Бантова М.А., Бельтюкова Г.В. Методика преподавания математики в начальных классах. – М.: Просвещение, 1984. – 335 с.
2. Богданович М.В. та ін. Методика викладання математики в початкових класах: Навч. посібник / М.В. Богданович, М.В. Козак, Я.А. Король. – К.: А.С.К., 1999. – 352 с.
3. Богданович М.В. Методика розв’язування задач у початковій школі: Навч. посібник. – 3-те вид., перероб. і допов. – К.: Вища шк., 1990. – 183 с.
4. Богданович М.В. Урок математики в початковій школі: Посібник для вчителя. – К.: Рад. шк., 1990. –192 с.
5. Боцманова М.Э. Психологические вопросы применения графических схем учащимися начальной школы // Вопросы психологии. – 1960. – №5.
6. Истомина Н.Б. и др. Практикум по методике преподавания математики в начальных классах: Учеб. пособие для студентов пед. ин-тов по спец. № 2121 «Педагогика и методика нач. обучения» / Н.Б. Истомина, Л.Г. Латохина, Г.Г. Шмырева. – М.: Просвещение, 1986. – 176 с.
7. Истомина Н.Б. Активизация учащихся на уроках математики в начальных классах: Пособие для учителя.– М.: Просвещение, 1985. –
8. – 64 с.
9. Истомина Н.Б. Методика обучения математике в начальных классах: Учеб. пособие для студ. сред. и высш. учеб. заведений. – 2-е изд., испр. – М.: Издательский центр «Академия», 1998. – 288 с.
10. Крутецкий В.А. Психология математических способностей школьников – М.: Просвещение,1968. – 432 с.
11. Методика начального обучения математике / под ред. Л.Н. Скаткина. – М.: Просвещение, 1972. – 320 с.
12. Методика начального обучения математике: Учеб. пособие для пед. ин-тов / В.Л. Дрозд, А.Т. Касатонова, Л.А. Латотин и др.; Под общ. ред. А.А. Столяра, В.Л. Дрозда. – Мн.: Выш. шк., 1988. – 254 с.
13. Методика преподавания математики в средней школе. Частная методика / сост. В.И. Мишин. – М.: Просвещение, 1987. –416 с.
14. Моро М.И., Пышкало А.М.. Методика обучения математике в 1-3 классах. – М.: Просвещение, 1975. – 336 с.
15. Пойа Д. Как решать задачу. – М.: Учпедгиз, 1959. – 216 с.
16. Стойлова Л.П., Пышкало А.М. Основы начального курса математики. – М.: Просвещение, 1988.– 320 с.
17. Формирование элементарных математических представлений у дошкольников / под редакцией А.А. Столяра. – М.: Просвещение, 1988. – 303 с.
18. Фридман Л.М., Турецкий Е.Н.. Как научиться решать задачи: Кн. Для учащихся ст. классов сред. шк. – 3-е изд., дораб. – М.: Просвещение, 1989. – 192 с.
19. Эрдниев П.М., Эрдниев Б.П. Теория и методика обучения математике в начальной школе. – М.: Педагогика, 1988. – 208 с.
Дополнительная литература
20. Метельский Н.В. Дидактика математики: общая методика и ее проблемы. [Учеб. пособие для вузов] – 2-е изд., перераб. – М.: Изд-во БГУ, 1982. – 256 с.
21. Лысенкова С.Н. Когда легко учиться: из опыта работы учителя начальных классов № 587 г. Москвы / Предисл. И.Д. Зверева. – М.: Педагогика, 1981.–144 с.
22. Шаталов В.Ф. Эксперимент продолжается.–Д.: Сталкер, 1998. – 400 с.
23. Эрдниев П.М., Эрдниев Б.П. Укрупнение дидактических единиц в обучении математике: Кн. для учителя. – М.: Просвещение, 1986. – 255 с.
24. Эрдниев П.М., Эрдниев Б.П. Обучение математике в школе / Укрупнение дидактических единиц: Кн. для учителя. – 2 изд. испр. и доп. – М.: АО «Столетие», 1996. – 320 с.
Учебники математики для начальных классов
[Б1] Богданович М.В. Математика. Проб. підруч. для 1 кл. тририч. початк. шк. – К.: Освіта, 1996. – 206 c.
[Б2] Богданович М.В. Математика. Підруч. для 3кл. чотириріч. і 2 кл. тририч. початк. шк. – К.: Освіта, 1995. – 224 c.
[Б3] Богданович М.В. Математика. Підруч. для 4 кл. чотириріч. і 3 кл. тририч. початк. шк. – К.: Освіта, 1995. – 240 c.
[А1] Аргинская И.И., Занков Л.В. Математика: 1 кл.: Проб.учеб. – 4-е изд. – М.: Просвещение, 1994. – 192 с.
[А2] Аргинская И.И. Математика: 2 кл.: Проб.учеб.– М.: Просвещение, 1992. – 191 с.
[А3] Аргинская И.И. Математика: 3 кл.: Проб.учеб. – 2-е изд. – М.: Просвещение, 1994. – 159 с.
[М1] Моро М.И., Бантова М.А., Бельтюкова Г.В. Математика: Учеб. для 1 кл. трехлет.нач.шк. –14-е изд. – М.: Просвещение, 1991. – 176 с.
[М2] Моро М.И., Бантова М.А. Математика: Учеб. для 2 кл. трехлет.нач.шк. – 19-е изд. – М.: Просвещение, 1991. – 256 с.
[М3] Математика: Учеб. для 3 кл. трехлет.нач.шк. / А.С. Пчелко, М.А. Бантова, М.И. Моро, А.М. Пышкало – 16-е изд. – М.: Просвещение, 1987. – 207 с.
http://www.pedlib.ru/katalogy/katalog.php?id=1&find_me=!%CE&page=1
Оглавление
Введение. Роль и функции текстовых задач в обучении математике
Понятие текстовой арифметической задачи
Структура текстовой задачи
Различные методические подходы к первому знакомству с задачами
Что значит решить задачу?
Понятие простой и составной задачи
Понятие задач одного вида
Основные приемы работы над задачами одного вида
Этап подготовки к введению задач данного вида
Этап ознакомления с задачами данного вида
Этап закрепления умений решать задачи данного вида
Способы решения текстовых задач
Основные этапы решения задач
Изучение текста задачи и его анализ
Поиск способа решения
Краткая запись и другие виды графической работы с задачей
Синтетический и аналитический методы решения задач
Способы рассуждений при разборе задач
Решение задачи, способы записи арифметического решения задачи
Проверка решения задачи
Последующая и творческая работа над задачами
Развивающие функции задач в обучении математике в начальных классах
Задачи с недостающими или избыточными данными, нереальные задачи
Работа над деформированными задачами
Формы организации учебно-познавательной деятельности учащихся при работе над задачами
Дифференцированная работа над задачей
Различные подходы к типологии учащихся при организации уровневой дифференциации при работе над задачами
Дифференцированная работа над краткой записью задачи
Дифференцированная работа над задачами нового вида
Дифференцированная работа на этапе закрепления навыков решения задач данного вида
Приемы дифференцированной помощи при самостоятельной работе над текстовой задачей
Дифференцированная работа над задачей при проверке домашнего задания
Вопросы и указания для самостоятельной работы
Вопросы для самоконтроля
Тестовые задания
Список использованной литературы
Основная литература
Дополнительная литература
Учебники математики для начальных классов
Введение. Роль и функции текстовых задач в обучении математике
Решение текстовых задач играет в математическом образовании очень важную роль. Одним из основных показателей глубины усвоения учащимися учебного материала и уровня математического развития является умение решать задачи, текстовые в том числе. Поэтому обучению решению текстовых задач уделяется много внимания, программами выделяется большое количество часов на решение текстовых задач.
Согласно программе, работа над текстовыми задачами в начальной школе занимает около 60% времени. Задачи выступают и целью обучения и его способом. Посредством задач у учащихся формируются математические понятия, исследуются математические законы. Задачи являются средством развития логического мышления, показывают значение математики в повседневной жизни, помогают детям использовать полученные знания в практической деятельности.
Ведущие методисты отмечают, что решение текстовых задач в начальной школе преследует двойную цель: с одной стороны – научить решать текстовые задачи различных видов, с другой стороны – сами текстовые задачи выступают как средство обучения, воспитания и развития школьников. (СНОСКА: Далее термины «текстовая задача» и «задача» будем использовать как синонимы)
Однако, к сожалению, до сих пор, чаще всего для обучения детей решению задач учителями употребляется лишь показ способов решения определенных видов задач и закрепление их решения механически, хотя решение задач призвано, с первых шагов знакомства с ними, развивать логическое мышление, смекалку, сообразительность; в работе с задачами совершенствуются логические умения проводить анализ и синтез, обобщать и конкретизировать, раскрывать основное, выделять главное в тексте и отбрасывать несущественное, второстепенное; воспитывать личностные качества – терпение, настойчивость, волю.
Нельзя не отметить и тот факт, что часто при решении задач у учащихся также пробуждается интерес к самому процессу поиска решения, при достижении цели дети получают моральное удовлетворение (при правильной организации работы над задачей). При решении задач дети разных возрастов получают новые знания, обобщают и систематизируют полученные ранее.
В начальной школе именно в процессе решения задач происходит формирование различных математических понятий. «Используемые в текстовых задачах житейские понятия и представления являются исходным материалом для формирования первоначальных абстракций и математических понятий у учащихся. С другой стороны, такие задачи позволяют учащимся видеть за математическими понятиями и отношениями вполне реальные, жизненные явления» [11, с.158].
Например, формирование понятий сложения и вычитания происходит в системе целесообразно подобранных задач, которые решаются при помощи предметно-практической деятельности. Дошкольники знакомятся со смыслом действий сложения и вычитания именно на основе решения простых задач на нахождение суммы и остатка, теоретической основой которых являются операции объединения непересекающихся множеств и удаления части множества.
В соответствии с действующей программой в начальной школе все арифметические действия вводятся именно в задачах, т.е. формирование конкретного смысла арифметических действий (понятие сложения, вычитания, умножения, деления) происходит именно в процессе решения задач.
В системе задач также проводится пропедевтика функциональной зависимости, более глубокое закрепление идеи которой происходит в старших классах.
Решение задач также повышает вычислительную культуру учащихся. В процессе решения текстовых задач у учащихся формируются умения и навыки моделирования реальных объектов и явлений, перевода на математический язык реальных жизненных ситуаций.
В школе первой ступени закладывается фундамент знаний, умений и навыков учащихся, необходимых не только для их дальнейшего образования, но и для развития умственных, моральных и эмоционально-волевых качеств личности учащихся. Курс начальной математики имеет ярко выраженную практическую, учебно-познавательную направленность, способствует формированию обобщенных приемов умственной деятельности учащихся.
В обучении младших школьников решению задач учителю начальных классов необходимо обратить внимание на целенаправленное формирование у каждого учащегося следующей структуры умений (В.А. Мизюк)
Дата: 2018-12-28, просмотров: 2042.