Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Особенность СУ ТО состоит в том, что выходные параметры системы

//,{/) = |Я,(/), Я₂(/), ..., НМ\

где Т~ знак транспонирования, не определяются однозначно вход­ными параметрами

С«) = |<7,</), <?₂(/), ..., С,(/)|^г,

а зависит от ряда переменных Z { t ), определяемых ее собственными характеристиками,

Z ( t ) = |z,(/), ш, ..., Ш\^т.

В итоге выходные параметры СУ ТО определяются как

н,{1) = Ф\гм, ио, .... z_n { t ), с,(/), с₂(0, ..., G_q ( t \ /],

/= 1, 2, ..., m ,

где H ,{ t ) (i = 1, 2, ..., m ) — параметры, характеризующие функци­онирование СУ и представляющие интерес для проектировщика СУ ТО; G ,{ f ) (/= 1, 2,..., q ) — воздействия, влияющие на поведе­ние объекта; Ф, — однозначные функции.

Изменение H ,{ t ) на интервале (r₀, t_k ) определяется изменением G ( t ) на том же интервале и начальными условиями \ Z _{ ( t ₀ ), ^(/₀),..., ZM \, т.е.

Я,<» = ФДВД, Z₂0b),..., Z„(/₀), C,(/b,/*), G&o, /*),..., G₉(/₀, /*), /I,

' e (f₀, t_k ).

Минимальное число п переменных Z „ которые позволяют од­нозначно выразить выходные параметры СУ Н, (/ = 1, 2, ..., ш) через ее входные параметры С, (/' = 1, 2,..., q ) и время t , представ­ляют собой переменные состояния СУ. Состояние СУ содержит

249

всю информацию о про/илом, необходимую для однозначного определения реакции Н ( t _{) , t_k ) на произвольный входной сигнал G ( to , <*)• В свою очередь, сами переменные состояния Z \((), Z ₂ ( i ),..., Z_n ( t ) в любой момент времени / е (/₀, /*) являются однозначны­ми функциями начального состояния Z ( t ₀ ) и реализации входа G('o, 4):

//,</) = F\Z_x(k), Z&u, ..., Z „(t₀), Ci(/₀, /*), $0b, /*), -, <7₄(/₀, /*), /J,

или в векторной форме

Для СУ, динамические свойства которой описываются линей­ными дифференциальными уравнениями, уравнения ее состоя­ния можно записать в следующем виде:

Z ( t ) = AZ ( t ) + BG ( t ); H { l ) = CZ { t ) + UG { l ),

где А — матрица коэффициентов; В — матрица управления; С — матрица выхода; U — матрица обхода системы.

В случае стационарной системы элементы матриц коэффициен­тов, управления, выхода и обхода объекта являются постоянными. Для нестационарной СУ все или некоторые из элементов матриц, входящих в уравнения состояния, зависят от времени /. Эти урав­нения называют уравнениями состояния. Векторы H , G и Z называют соответственно вектор выхода, входа и состо­яния объекта. Считается, что вектор выхода Н принимает соот­ветствующие значения в пространстве состояния СУ с параметра­ми Z

Понятие переменных состояния используют и для описания входных сигналов. Для этого записывается следующее дифферен­циальное векторное уравнение:

V '~ PV , V = \ V_uV ₂ ,..., V_m \ T ,

решение которого V ( f ), te (0,/), полученное при определенных начальных условиях Уф), однозначно определяет вектор входа

u ( t ) = DF ( t ), te [0, t ],

где D — матрица размером gxm .

Тогда поведение СУ, на которую действует входной сигнал U ( t ), представляется однородным векторным дифференциальным урав­нением

F(/) = /(z(/);/), z(0) = z₀,

где z ( t ) = | V ( t ), x ( t ) | — вектор состояния системы; 1(0) — вектор начального состояния.

250'

Считается, что вектор J принимает значение в расширенном пространстве состояний СУ z = xv , где V э v — пространство со­стояний входа СУ.

Для СУ с линейными параметрами уравнения состояния име­ют вид:

z (/) = Fz (0; y ( f ) = Nz { t ).

где F , N — расширенные матрицы соответственно коэффициентов СУ и ее выхода.

Существует ряд способов формирования уравнений состояния в процессе прямого, последовательного и параллельного програм­мирования. При нахождении этих уравнений удобно использовать схемы в переменных состояния.

Для представления динамических свойств линейных стационар­ных систем с одним входом «(f) и одним выходом у{() часто ис­пользуют передаточную функцию

] V ( S ) = ^- = ^{bmpm +} ^-'^""' ⁺ ~ + ^b\P + ^bo и(р)  р" +а„._хр^п'⁾ +...ла_хр + а₀

которую легко определить, если задано дифференциальное урав­нение системы в следующем виде:

d/"          d/"^-1               d/

, d^mu(f) . d^m-'«(0 , <iu{t) . ,_Л

Следует отмстить, что динамические связи в приведенных урав­нениях для объекта, имеющего сигналы на входе <?(/) и выходе Я(0, задаются единственным образом. Однако уравнения состоя­ния для одного и того же объекта не единственны и могут иметь разные матрицы А, В, С, II , или F . Элементы этих матриц зависят от способа получения схемы объекта в переменных состояния.

Процесс составления схем в переменных состояния часто на­зывают программированием. Такое название оправданно, так как используемые приемы полностью аналогичны как для непрерыв­ных, так и для импульсных систем. Схемы в переменных состояни­ях импульсных систем применяют для составления программ при моделировании на ЭВМ. Схемы в переменных состояниях для не­прерывных систем могут служить непосредственно для составле­ния схемы набора при моделировании на аналоговых вычисли­тельных машинах (АВМ).

При прямом программировании передаточная функция ТО записывается после деления числителя и знаменателя нар" в сле­дующем виде:

251

______ ш ______ ₌

b_mp-⁽"-^m) + ft_m-,P"^(n_m+n +... + b_tp-ⁱⁿ-ⁿ + boP~"

₌                  Hi £)                   

1+а„_,р^_| +... + а,р^Чп-^,) +а₀р-"'

Приравнивая правую и левую части к Е(р), получаем E ( p ) = G ( p )- a_n _ _l p - ^l FAp )-...- a_lp -< ⁿ -» E < j >)+ a ₀ p -" E ( p );

Н{р) = Ь_тр~^Е(р)₊Ь_т_₁р-1»-^т+»Е(р)₊...₊Ь₁р-^Е(р)+Ь₀Р-"Е(р).

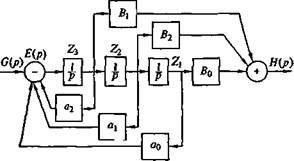
Эти уравнения применяют для составления схемы в перемен­ных состояния. На рис. 6.21, а показана схема для п = 3, т = 2.

Переменными состояния являются сигналы (Z₍, Z₂, Z,) на вы­ходе интеграторов. Если предположить, что £/(/) является ступен­чатой функцией U ₀ \( t ), то дифференциальными уравнениями для переменных состояния, показанных на рис. 6.21, о, являются:

С = О, Z \ = Z₂, Z₂ = Z₃, Z3 = (7- а₂-2з^- «i^2^{_ а}о^ь или

с		G
*2	= F	Z, z2
Z',		z3

0 0 0 0 0 10 0

0 0 10"

1 - а₀ -щ -а₂

Уравнение выхода имеет вид

//(/) = 6oZ, + b.Za + bjZ₃.

При параллельном программировании передаточная фун­кция представляется в виде суммы простейших дробей

1=1 Если все корни /?, (/ = 1, 2,..., п) характеристического уравнения

R " + a ^ R "-¹ + ... + а,/? + а₀ = О

действительны и различны, т.е.

то коэффициенты Л,- находят методом неопределенных коэффици­ентов. Схема для объекта W { p ) получается параллельным соедине­нием элементов. Для т = 2, п = 3 и разных действительных корней характеристического уравнения на рис. 6.21, б показана схема в

252

 

 

 

		Ол
C(J>)		"1

Н(Р)

 

Рис. 6.21. Структурные схемы математических моделей, построенные ме­тодами прямого (о), параллельного (б) и последовательного (в) про­граммирования:

(!{ р) — входной сигнал; Н(р) — выходной сигнал; Е{р) — разностный ситал;

Во, В,, В_ъ «о, о,, а₂, й₃. b , /?i, /?2, Лэ. Ц< ^2 — вычисляемые коэффициенты;

Z,—Zj — параметры состояния интегрирующих элементов

253

переменных состояния. При скачкообразном входном сигнале урав­нения состояния имеют следующий вид:

С = 0; Z\ = a_xG- R_xZu Z₂ = a₂G- R₂Z_2l Z₃ = a₃G- R₃Zj;

H = Z, + Zi + Z₃,

или

// =

 

G'		0 0	0	0		С
	=	A\ -R\ Ai 0	0 -R2	0 0	X	Я. Иг
И'г		Ai 0	0	-Ri		и,

Форму представления схем и уравнений состояния при парал­лельном программировании называют канонической.

В общем случае, когда характеристическое уравнение содержит комплексные корни, отдельные ветви схемы в переменных состо-

D - R + F -

яния (для слагаемых WAp ) = '   ^!—) строятся так же, как и

Р + RiP + Qi при прямом программировании. При наличии кратных корней

( P - Ri ) r ,/•>!) строятся последовательным про-

А-
отдельные ветви (для слагаемых вида W_t ( p ) =------- hrrr или

D , p + E ,

JVAp ) = -

граммированием.

При последовательном профаммировании передаточная функция представляется в виде произведения простейших дробей

W { p )^ flW ,{ p ). 1=1

Схема СУ (рис. 6.21, в) получается последовательным соедине­нием схем в переменных состояния, полученных для каждой пере­даточной функции Wiip ) (/= 1, 2,..., к):

_JV{p)= H{p) _b(_P-L_l)(p-L₂) _

< КР ) P<J>-R\)<J>-Ri)

b р - Ц p-Lj

А[_{1 +} л,_-а

R ,

P -

PP - RxP - R ₂ p

_ч р-Ъ

При постоянном входном сигнале уравнения состояния будут иметь вид

С = 0; Z \ = - R ₂ Z_X + ( R ₂ - L ₂ ) Z 2 + ( R ₃- Z₃)Z₃; Z₂' = - R & + (Л, -LJZ ,;

Z'₃ = bG; H^Z^ + Zi + Zs

254

или

//' =

G '

А z ₃

0 0 0           0

О — R . i /?2 ^— 1-ъ Ri ~ [*1

о

о о - я, я, - ц

АО     О

G

z ₂

Z ,

#=|0 1 I \\ Н .

Нетрудно заметить, что уравнения состояния будут другими при иной последовательности соединения элементов Wfjj ), например, если элемент b /р поставить не на входе, а на выходе объекта. Зтот факт лишний раз подтверждает возможность широких вариаций математических моделей ТО с целью выбора удобных для исследо­ваний зависимостей между переменными состояния.

При моделировании динамических процессов с помощью ЭВМ следует приведенные ранее матрицы представить в виде следую­щей матрицы перехода:

Ф (/) =

йи(/) an(t) ai\(t) an(t)

Qm\{t)  (l_ml{t)

a. „ (0 | ain(t) I

a , m ( t ) |

где a ₀ ( f ) — выражение для реакции на единичный скачок в точке / при возбуждении схемы в точке у.

В качестве примера рассмотрим контурную фрезерную обработ­ку на станке с ЧПУ, которая имеет общие черты с обработкой сложного профиля на токарном станке с ЧПУ. Формообразование контура происходит за счет согласованного во времени относи­тельного движения заготовки и инструмента по взаимно-перпен­дикулярным направлениям.

Управление перемещениями при обработке контура осуществ­ляется с помощью СЧПУ. Характерными случаями являются обра­ботка элемента контура в виде дуги окружности (рис. 6.22, а), об­работка элемента контура в виде прямой (рис. 6.22, б), а также варианты обработки элементов в виде изломов траектории (рис. 6.22, ей г). Достижение соответствия контура, полученного в результате обработки, контуру, заданному по программе, являет­ся основной технологической задачей.

При обработке контура, имеющего произвольную геометрию, динамические ошибки системы существенно зависят от геометрии каждого участка контура, его положения в осях координат станка, а также от величины контурной скорости. Последнее обстоятель­ство используют для обеспечения точности контурной обработки.

255

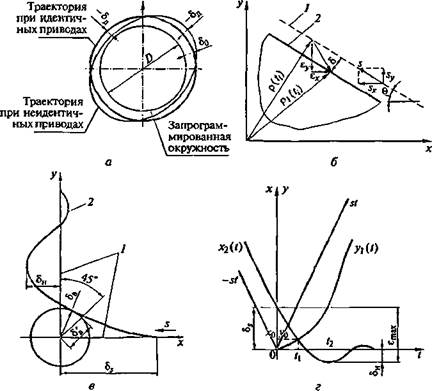
Рис. 6.22. Обработка контуров в виде окружности (а), отрезка прямой (б), углов — прямого (в) и произвольного по величине (г):

D — диаметр обрабатываемой окружности; s , s „ s_y — соответственно контурная скорость и ее составляющие по осям х и у, 1,2 — траектории движения инстру­мента; / — время; /_ь t - i — текущие моменты времени; +5_Л и -8_Л — отклонения размеров детали при неидентичных приводах; б<> — отклонения размеров при идентичных приводах; р(/,), Р](/<) — радиусы-векторы соответственно до задан­ной / и полученной 2 траектории; 6 — угол наклона траектории; 6 — величина погрешности обработки контура; е_х, е_у — величины рассогласований соответ­ственно по осям х и у, 8_Н — наружная погрешность обработки; 6„ — внутренняя погрешность обработки; 8', — проекция величины внутренней погрешности; 6₅ — отрезок контура, на котором присутствует noi-решность обработки

Снижая величшгу контурной скорости, уменьшают величину ди­намической ошибки и таким образом уменьшают отклонения раз­меров на контуре. Как правило, занижают величину контурной скорости вдоль всего контура, хотя при этом неоправданно сни­жается производительность обработки.

Прогнозирование точности контурной обработки на стадии проектирования ТП обработки позволяет определить участки кон­тура, на которых необходимо принять меры к снижению отклоне-

256

ний размеров. При этом, варьируя известными методами сниже­ния отклонений размеров, по имеющейся информации о процес­се формообразования контура повышают производительность об­работки при обеспечении требуемой точности.

При разработке ММ с использованием метода пространства состояний следует иметь в виду, что при описании процессов кон-1урной обработки достаточный порядок дифференциального урав­нения, описывающего динамические характеристики объекта из условия точности ММ, составляет п = 3. При использовании мето­дов параллельною и последовательного программирования полу­чают матрицы с некоторыми нулевыми компонентами (разрежен­ные матрицы), что упрощает расчет на ЭВМ, однако метод после­довательного программирования предполагает построение СУ с апериодическим законом изменения выходного параметра, что при обработке контура не используется. Использование колебательно­го процесса предполагает использование метода параллельного про­граммирования.

Математическую модель процесса формирования контура пу­тем относительного движения заготовки и инструмента в процессе формообразования контура по каждой из координат можно пред­ставить в виде следующего дифференциального уравнения:

1\ Т_г ^ f + (7; + Г₂)^~ + К(Т₃ + 1)^ + КН = К('/\ + ту)^ + KG ,

где И— выходное воздействие; С— входное воздействие; Т_ь Т₂, Т₃ — постоянные времени динамической системы; К — коэффи­циент усиления динамической системы; г\ — коэффициент введе­ния производной по управляющему воздействию.

Параметр ц определяет информацию о скорости перемещения но отдельной координате и не определяет информацию о величи не перемещения.

Анализ точности получаемого контура целесообразно прово­дить рассматривая погрешность как отклонение размеров в каж­дой точке заданного контура (рис. 6.23). Располагая методикой рас­чета положения точек полученного контура, легко в автоматичес­ком режиме проводить анализ процесса формообразования конту­ра.

Для определения положения точек полученного в результате обработки контура необходимо решение дифференциального урав­нения для каждой из координат. Здесь нужно иметь в виду, что решение его традиционными методами связано с серьезными труд­ностями. Во-первых, решение необходимо выполнять для каждой точки контура с шагом, равным дискрете системы управления, обеспечивающей управление процессом формообразования. Во-вторых, решать указанные дифференциальные уравнения необхо­димо при ненулевых начальных условиях. С учетом того, что урав-

9 За* 519

257

Л .

Ук

/

/

/ F_{7 i}

* a

Рис. 6.23. Общий случай обработки кон­тура произвольной геометрии:

/ — контур, получаемый при обработке; 2 — допустимое отклонение размеров на конту­ре; 3 — контур, заданный по программе; F ,— точки получаемого контура; Q -, — точки за­данного контура; в_г, 6з — величина и направ­ление смещения точек заданного конту­ра в сторону полученного контура

нение окружности описывается дифференциальным уравнением второй степени, в целом указанные уравнения могут иметь пятый порядок.

Решение поставленной задачи оказывается практически невоз­можным даже при использовании ЭВМ большой мощности. Обычно при разработке ТП используют вычислитель! гые устройства малой мощности. В свете этого желательно иметь методику, позволяю­щую решать поставленную задачу средствами малой вычислитель­ной техники.

Используя преобразования Лапласа, можно получить переда­точную функцию Ф(р), характеризующую динамические харак­теристики системы по каждой из координат. В общем виде переда­точная функция имеет вид

Ф(/0

(7з + г\)Кр + К

Т_хТ_гР> + (Г, + Т₂)р² + К(Г_Ъ + \)р + А"

где р — оператор Лапласа.

Для каждой из координат структура функции сохраняется. Раз­личия состоят лишь в значениях коэффициентов, составляющих функцию.

Рассматривая выходной параметр И как значение координаты, в общем виде для него можно записать следующие выражения:

для случая обработки элемента контура в виде отрезка прямой

_я=£___________ Кр(Т₃+г)) + К_________ .

Р Т_{Т₂р³ + (7J + Т₂)р² + К(Т₃ + \)р + К' для случая обработки элемента контура в виде дуги окружности

II _ ыр_________ Кр(Т_г\т\) + К_________

р² + со² Т{Г₂р* + (Г, + Т₂)р² + К(Т₃ +\)р + К' где s — контурная скорость; со — круговая частота.

258

Представим второй дробный сомножитель правой части в виде простейших дробей. Для этого приведем выражение в знаменателе к «неполному» виду

Т²р^ + 2^Тр² + р+К=0,

где 7Д — промежуточные коэффициенты.

Разделив почленно компоненты уравнения на Т², получим

р^ъ + — р² + -£г + -^ = 0.
7"             Г 7*

Подстановкой ^ = ^ - —^ приводим уравнение к виду

где rf = -с²/3 + £; 9 = 2(а/3)³ - flfc/З + с; а = 2^/Г; Ь = 1/Г²; с = АГ/Г². Корни «неполного» кубического уравнения

Y ,= A + В

2

Y_ur .- d ±*±^*>

A = fUS -, B ^ ff ^; e = ^

где _Л = a~i*vo; ^ = _A3j-^.-ve; « = l|l +[|

Формирование ММ, описывающей поведение рабочего органа станка по каждой из координат, можно проводить одним из трех методов: прямого, последовательного или параллельного програм­мирования.

Применим метод параллельного программирования. Преобра­зуем выражение для выходного параметра, используя метод нео­пределенных коэффициентов. В окончательном виде передаточная функция будет следующей:

^КР) р-Е< (р-М)² + £?' где £_ь Ёг, £_3> £4 — коэффициенты:

_{F   р}         К+г)Е_{4              р} _ r){M² + L²)-KE< + 2MK

'    ² M²+L²-2ME<+p²' ³     N-2M_Pl+El

Для разработки ММ процесса формообразования необходима структурная схема динамических процессов, протекающих по каж­дой из координат. На рис. 6.24 представлена структурная схема ММ для каждой координаты, построенная на основе выражения, по­лученного методом параллельного программирования.

9'

259

! Р	У	ш
ГГ ^_		ГП
1 р		Ш

Используя построенную струк­турную схему, опишем связи меж­ду выходами интегрирующих зве­ньев динамической системы. Для этого используют передаточные функции, связывающие выходы интегрирующих звеньев. Отдель­ным передаточным функциям присвоим двухзначные индексы, в которых первая цифра означает номер точки, где происходит на­блюдение реакции системы на ее возбуждение, вторая — номер точ­ки возбуждения системы единич­ным скачком.

Например, функция, описыва­ющая взаимосвязь между точками 3 и 2, имеет виц

Рис. 6.24. Структура математиче­ской модели формообразования по каждой из коогчинат: Z( j>) — выходной сигнал, р — опе­ратор Лапласа; М, N , £,. Е2, Л."3, А"4 — коэффициенты модели; м, — угло­вая скорость; /, 2, 3, 4, 5, 4\ У — вы­ходы интегрирующих звеньев

Wn { p ) -

-Np + 2MN р² - 2Мр + N '

где N = M ² + L ² .

Аналогично описываются пере­даточные функции для связей между другими точками динами­ческой системы. Для описания функций a_m ,( t ), определяющих вид переходных процессов, протекающих в каждой точке системы под действием возбуждения этой системы в разных ее точках, имеем в виду, что возбуждение осуществляется единичными скачками вила

G ( p ) = \/ p .

Применяя обратные преобразования Лапласа для функций W „ _m ( p ) и С(р), можно получить законы изменения выходных ве­личин а_тп(р) во всех точках динамической системы. Например, для точек 3 \\ 2 выражение для функции a ^( t ) имеет вид:

йзг(0 = L-

-Np + 2MN p(p²-2Mp+N)

N = 2 М ~ е *"

sin

7J-2arctg-^ M

Подставив в полученные выражения значение времени /, в те­чение которого при заданной контурной скорости совершается взаимное перемещение инструмента и заготовки на одну дискрету системы управления, получим числовые коэффициенты а„_т(р), ха­рактеризующие изменение состояния динамической системы во всех ее точках за указанный период, и запишем их в виде матрицы

260

o„ a_n ... й,₅ _ o₂| c₂₂ ... a₂₅

a₅₁ a₅₁ ... a₅₅

При моделировании протекающих в динамической системе ре­альных процессов, связанных с контурной обработкой, возбужде­ние необходимо осуществлять скачками возбуждающих воздей­ствий, обычно отличающихся от единичного на некоторую вели­чину. Значения скачков возбуждающих воздействий можно пред­ставить в виде произведения единичного скачка и некоторой фун­кции Z_m ( t ).

Для определения значения этой функции для точки т динами­ческой системы можно воспользоваться выражением

Z_m { t ) = ^ Zj ( t - M ) a_mj .

Таким образом, выражение для матрицы состояния выхода ди­намической системы может быть определено через матрицы коэф­фициентов и состояния выхода динамической системы

 

Z,(t)		Z,(/-A/)
z2(t)	= Лх	Z2(/-A/)
Zs(/)		25(/- Л /)

Информацию о состоянии динамической системы можно по­лучить с шагом, равным М. Точность расчетов будет тем выше, чем меньше величина Л/, но, в то же время, при расчете процесса формообразования контура с уменьшением величины Д/ растет число шагов, а следовательно, возрастает объем вычислений. Ис­следования показывают, что оптимальным является выбор значе­ния Д/, равного величине дискреты системы управления, делен­ной на величину контурной скорости.

Таким образом, состояние динамической системы в каждый момент времени можно свести к осуществлению элементарных арифметических действий над известными численными значения­ми коэффициентов матриц, описывающих свойства динамичес­кой системы. Это принципиально упрощает расчеты, связанные с определением положения контура, получаемого в результате про­текания процесса формообразования. Полученная структурная мо­дель динамических процессов позволяет осуществить моделирова­ние процессов при необходимости на аналоговых вычислительных машинах.

261

Окончательно уравнение выхода для одной координаты имеет вид

//(О = Z,(0E, + ШЕ₂ + ШЬ,

где Н{1) — значение координаты в текущий момент времени /.

При расчетах по приведенной методике на первом этапе рас­считывается матрица коэффициентов динамической системы. Да­лее, путем приращения параметра t с шагом Д/ определяются ко­ординаты точек F_h составляющих получаемый в результате про­цесса формообразования контур (см. рис. 6.23), и координаты то­чек Q , контура, заданного по программе. Последовательно осуще­ствляя расчет вдоль по каждому из этих контуров, можно легко определить наикратчайшие расстояния отточек контура, заданно­го по программе, до точек контура, полученного в результате про­текания процесса формообразования.

Если точки полученного контура отстают от точек заданного по программе в пределах величины допуска, то на этих участках усло­вие обеспечения точности выполняется. В тех точках, где получен­ный контур выходит за установленные пределы, требуется при­нять специальные меры по изменению траектории получаемого контура.

В связи с тем, что отклонения размеров существенно зависят от расположения контура в осях координат станка, необходимо при проектировании ТП контурной обработки определять оптималь­ное положение заготовки на столе станка. Для этого необходимо, используя разработанную методику, определить отклонения раз­меров во всех точках заданного по программе контура и просум­мировать их.

Физическим смыслом полученной величины является площадь фигуры, образованной отклонениями размеров. При варьирова­нии угла поворота заготовки в осях координат станка площадь бу­дет меняться. Оптимальным положением заготовки на столе стан­ка должно считаться такое, при котором площадь указанной фи­гуры минимальна.

При расчетах отклонений Q размеров на контуре можно ис­пользовать формулу

Q = 4{ F_x - Q_x )* + { F_y - Qy )\ где Qx , Qy — координаты некоторой точки контура, заданного по программе; F_x , F_Y — координаты ближайшей к этой точке точки полученного контура.

Суммарная погрешность па контуре составит

где Qi — отклонение размера от заданного в /-й точке контура.

262

Условие оптимального положения заготовки на столе станка записывается в виде

£)_Е—» min.

Условие определения оптимального положения заготовки на столе станка позволяет сократить протяженность участков конту­ра, на которых величина отклонений размеров превышает задан­ную величину. Используя предлагаемую методику расчета откло­нений размеров для сокращения их величин, можно применить процесс управления по скорости. В этом случае изменение контур­ной скорости оказывается минимальным, что приводит к повы­шению производительности обработки по сравнению с традици­онными методами обеспечения точности.

6.7. Оптимальное управление технологическими объектами

При разработке автоматических СУ ТО прежде всего ставится следующая задача: система должна выполнять свое назначение, определяемое целью управления. Иногда стоит более сложная за­дача разработать СУ с наилучшими показателями качества. Для разработки таких СУ применяют принцип оптимальности, позво­ляющий обеспечить наилучшее выполнение цели управления.

Аитоматическую СУ, обеспечивающую наилучшие технические или технико-экономические показатели качества при заданных условиях работы и ограничениях, называют оптимальной. Оценку достижимости цели в процессе управления ТО, представ­ленную в формализованном виде (аналитической форме), приня­то называть критерием оптимальности, который представляют в виде целевой функцией. Разработка наилучшей СУ, удовлетворя­ющей поставленным требованиям, представляет собой задачу син­теза оптимальной системы.

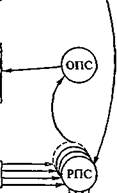
Возможны два основных типа задач синтеза оптимальных СУ ТО. В задачах первого типа известна структура СУ ТО (передаточные функции регулятора К_р(р) и ТО Ко(р)), требуется найти оптималь­ное значение ее числовых параметров, при которых обеспечивается экстремальное значение заданного показателя качества (синтез па­раметров СУ ТО). В задачах второго типа СУ полностью неизве­стна и требуется определить ее структуру и параметры так, чтобы она была оптимальной по принятому показателю качества (синтез структуры СУ). На практике обычно задан объект управления, по­этому задача синтеза состоит в определении структуры и парамет­ров оптимального управляющего устройства (УУ) (рис. 6.25).

Переменные выхода y ( f ), управления «(/), входных х_вк(() и воз­мущающих /_в(0 воздействий в обшем случае могут быть как ска­лярными, так и векторными величинами.

263

h.

-=<&-

\ --------- \ и \ —■— t

 

 

 

	УУ	f/	|/.
1	?		Ko(P) —
t

Рис. 6.25. Структурная схема систем управления:

а — с известной структурой; 6 — с неиз­вестной структурой; A",,, Y — входной и выходной параметры;^ — функция, опи­сывающая внешние возмущающие воз­действии; U — выходной сигнал регуля­тора; K_v ( j >) — передаточная функция ре­гулятора; УУ — управляющее устройство; К„(р) — передаточная функция техноло­гического объекта

Наиболее распространенной является задача определения опти­мальных управлений «(/), обеспечивающих оптимальные процес­сы в функции времени при заданных начальных Y { t ₀ ) и конечных К(/_к) значениях выходных переменных. Оптимальные управления «(/) ТО и их реализацию различают для двух основных случаев: без применения (разомкнутая СУ) и с применением (замкнутая СУ) обратных связей. В разомкнутой оптимальной СУ (рис. 6.26, а) уп­равляющее устройство по заданным граничным условиям форми­рует оптимальный закон управления. При этом координаты ТО не используются в формировании закона управления. В замкнутой оптимальной СУ (рис. 6.26) на вход УУ подаются соответствую­щие сигналы с выхода ТО.

Решение задачи синтеза оптимальной системы управления на­чинают с описания реальных элементов системы математически­ми соотношениями (состаапение ММ системы). Далее устанавли­вают имеющиеся ограничения для координат системы и анализи­руют характеристики сигналов внешних воздействий, а также со­ставляют математическое выражение заданного критерия качества.

После того как задача синтеза математически сформулирована, ее решают соответствующими математическими методами, в ре­зультате чего находят функцию управления из условия минимума или максимума показателя качества, определяющего оптималь­ный режим работы ТО.

то

то

У (' о )-

* „ <0

 

УУ

1/(0

«СГЛ»)

УУ

б

ПО

, Г(0

Рис. 6.26. Структурная схема системы оп­тимального управления:

а — разомкнутой; б — замкнутой; ТО — тех­нологический объект; УУ — управляющее ус­тройство; Л"_ю(0 — функция, описывающая входной сигнал; У(1₀) — заданные начальные значения выходных переменных; Y ( Q — ^то же, конечные; (/(У, Х_т) — оптимальное уп­равляющее воздействие; 1/(0 — функция сиг­нала управления регулятора; Y { f ) — функция выходного параметра

264

Аналитическое решение задачи синтеза оптимальных систем управления выполняют методами теории оптимального управле­ния. В результате находят аналитическое выражение, определяю­щее структуру и параметры УУ.

В простых задачах управления стационарными объектами при отсутствии внешних возмущений можно ограничиться таким ал­горитмом оптимального управления, который определяет неиз­менную настройку оптимального регулятора (управляющего уст­ройства). При этом предусматривается наличие достаточного объе­ма предварительных сведений (априорной информации) о внут­ренних и внешних условиях работы объекта и системы. Чем полнее на стадии проектирования априорная информация о характерис­тиках системы и условиях ее работы, тем точнее СУ, полученная в результате проектирования. Зто означает, что в данном случае оп­тимизируется только конструкция системы с целью обеспечения оптимальных процессов.

Существует большой класс объектов управления, статические и динамические характеристики которых изменяются в широких пределах заранее непредвиденным образом; при этом невозможно описать физические процессы, протекающие в них при функцио­нировании СУ в реальных условиях. В связи с этим для нестацио­нарных объектов СУ будут работать в условиях неопределенности, т.е. недостаточности («неполноты») априорной информации о ха­рактеристиках управляемого процесса.

Дальнейшее совершенствование производственных и техноло­гических процессов обусловлено усложнением задач управления. Специфическая особенность этих усложнений заключается в прак­тической невозможности подробного изучения и описания про­цессов, протекающих в СУ. По мере усложнения задач, возлагае­мых на СУ из-за уменьшения априорной информации о системе, появляются трудности в обеспечении заданного качества управле­ния. Для преодоления этих трудностей при разработке СУ, функ­ционирование которых происходит в условиях неопределенности, применяют принцип адаптации. Это позволяет искусственно со­здать эффект приспособления к изменяющимся условиям в СУ за счет того, что часть функций по получению, обработке и анализу недостающей информации об управляемом процессе осуществля­ется самой системой в процессе се нормальной эксплуатации с помощью адаптивного управляющего устройства (АУУ), а не про­ектировщиком на предварительной стадии разработки системы. Это позволяет существенно снизить влияние неопределенности на ка­чество управления и скомпенсировать в определенной степени недостаток априорной информации об управляемом процессе на стадии проектирования.

Системы управления, в которых параметры управляющих воз­действий или алгоритмы управления автоматически и целенап-

265

Рис. 6.27. Структурная схема формирова- г 1.\     ния сигналов управления в адаптивной

U( YXXB) d

ХвЛО

у. .                 систем управления:

 

	AVV		*(/)	ТО
	■	.

ЛУУ — комплекс измерительных, преобразо­вательных и вычислительных устройств, а так­же усилительных и исполнительных элементов; ТО — технологический объект; Х_ЛХЦ) — функ­ция, описывающая входной сигнал; У(/) — функция, описывающая выходной сигнал; Х(г) — функция сигнала цепи обратной связи; U ( Y , X , Х_вх) — функция комплекса сигналов управления технологическим объектом

равленно изменяются для осуществления в каком-либо смысле наилучшего управления ТО (причем характеристики ТО или воз­действий внешней среды могут изменяться заранее непредвиден­ным образом), называют адаптивными СУ.

Развитие новых технических средств радиоэлектроники, вычис­лительной техники и технической кибернетики, а также изучение и моделирование органов живых организмов способствуют созда­нию и совершенствованию адаптивных СУ. Обобщенная функцио­нальная схема адаптивной СУ показана на рис. 6.27, где АУУ в общем случае представляет собой комплекс измерительных, пре­образовательных и вычислительных устройств, а также усилитель­ных и исполнительных элементов.

Принцип адаптации применяют в тех случаях, когда сложность управляемого процесса (нестационарного объекта) достигает та­кого уровня, при котором влияние неполноты априорной инфор­мации об условиях работы системы становится существенным и невозможно обеспечить заданное качество процессов управления без приспособления системы к изменяющимся непредвиденным образом условиям функционирования.

Учитывая, что основным назначением всякой СУ является до­стижение требуемой цели управления в условиях, в общем случае заранее не определенных, их можно разделить на два класса:

• системы с жесткой настройкой, в которых неполнота инфор­мации не мешает достижению цели управления;

• адаптивные СУ, в которых неполнота информации не позволя­ет достигнуть цели управления с заданной точностью без автома­тического приспособления системы в условиях неопределенности.

СУ обоих классов можно строить таким образом, чтобы обеспе­чивались наилучшие показатели качества, т.е. в общем случае ука­занные классы систем могут быть оптимальными СУ с «жесткой» настройкой и адаптивными оптимальными СУ. При решении за­дачи синтеза оптимальной адаптивной СУ выбирают показатель качества, характеризующий достижение требуемой цели управле­ния в условиях неопределенности. Аналитическое решение задачи синтеза адаптивных систем выполняют соответствующими мето-

266

дами теории автоматического управления. Оптимизацию сложных СУ с помощью адаптивных управляющих устройств называют ав­томатической оптимизацией.

Таким образом, при разработке оптимальных адаптивных СУ ТО создают их оптимальную конструкцию, которая обеспечивает автоматическую оптимизацию в условиях неопределенности.

6.8. Развитие систем управления технологическими объектами

Развитие средств автоматики и электроники и прежде всего механизмов и устройств программного управления позволяет вы­полнять функции управления на качественно высоком уровне, а именно — управлять работой агрегатов с оптимизацией режимов их работы, адаптацией и самонастройкой режимов, придавая сис­темам управления не только функции исполнения разработанной программы, но в значительной степени и сам процесс програм­мирования.

При создании автоматических и автоматизированных систем различного назначения до недавнего времени в качестве их вычис­лительной основы широко использовали два класса средств циф­ровой техники:

• устройства с жесткой структурой, выполненные на базе циф­ровых логических схем;

• ЭВМ универсальные и управляющие.

Устройства с жесткой структурой обычно содержат большое чис­ло дискретных элементов и интегральных схем малой и средней степени интеграции. При этом различного рода изменения функ­ций требуют изменения схемы (т.е. перепайки соединений, заме­ны компонентов), проверочных тестов. Поэтому главным недостат­ком системы на основе таких устройств являются значительное время проектирования и изготовления, а также трудности внесе­ния изменений.

Системы на основе ЭВМ можно легко перестраивать с реализа­ции одной функции на другую, для чего достаточно составить и занести в память новую программу. Выполнение алгоритма функ­ционирования в таких системах осуществляется программно. При использовании серийных ЭВМ это значительно сокращает сроки проектирования, изготовления и настройки системы.

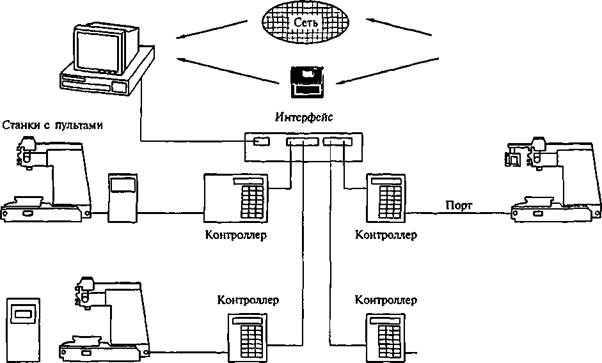
Использование ЭВМ в процессах управления ТО привело к появлению производственных систем, получивших название CIM (Computer integrated manufacturing), т.е. компьютеризированные интегрированные производства (рис. 6.28). Важнейшими компонен­тами таких систем являются подсистемы автоматизированного проектирования, а также программно-аппаратный интерфейс. Та-

267

го

00

 

 

Сервер

Станки с системами ЧПУ типа NC

 

Рис. 6.28. Схема компьютеризированной интегрированной прои

кая система //редстаачяет собой автоматизированный комплекс с гибко перестраиваемой технологией, в которой управление осу­ществляется от центральной ЭВМ. Она является системой более высокого уровня управления по отношению к каждой ЭВМ управ­ления ТО, входящих в такой комплекс, и обеспечивает максималь­ную и равномерную загрузку станков с помощью автоматизиро­ванных транспортных средств для деталей и режущих инструмен­тов и осуществляет «наблюдение» за ходом ТП (проведение контро­ля и ввод соответствующих корректив в работу ТО, изменение со­ответствующим образом технологических маршрутов обработки и при необходимости изменение заданных в программе параметров).

Электронно-вычислительная машина также осуществляет рас­пределение рабочих профамм, хранящихся в библиотеке профамм-ного обеспечения.

При этом, несмотря на то, что ЧПУ на базе ЭВМ имеет боль­шой объем собственной памяти, достаточной для хранения про­граммы на осуществление всего ТП, далеко не всегда рациональ­но передавать ее из ЭВМ в ЧПУ полностью из-за трудности кор­ректировки такими средствами.

Следующим более высоким уровнем автоматического управле­ния является обеспечение учета, планирования и диспстчирова-ния работы автоматизированного комплекса. Это по сути дела яв­ляется уровнем АСУ цеха или предприятия, которая реализуется также с помощью мощной ЭВМ, так как обычно адесь решаются более общие задачи, в том числе и задачи автоматизированной подготовки управляющих программ для ТО.

Такая многоуровневая СУ также включает задачи автоматиза­ции административного управления. Данную систему называют гибкой интефированной системой, при этом в случае необходи­мости ее более низкие уровни могут работать автономно.

Системы управления на базе ЭВМ строят также на основе мик­ропроцессора (МП). В МП объединены универсальные возможнос­ти профаммируемого средства с преимуществами и возможностя­ми, которые представляег технология микропроцессорной техники.

Формирование и развитие МП привело к появлению нового полхода к проектированию цифровых систем на основе профам-мируемой логики. Этот подход предполагает при построении сис­тем использование стандартных универсальных МП, работающих под управлением профаммы.

Если разработчик систем на основе устройств с жесткой струк­турой может пользоваться для r-ализации необходимых функций только аппаратными средствами, а при использовании ЭВМ — в большей степени только профаммными средствами, то при пост­роении СУ на основе профаммируемой логики он получает воз­можность использовать полностью как аппаратные, так и профамм-ные средства.

269

Необходимо отметить, что стоимость, малые размеры и масса, высокая надежность средств МП придают СУ новые качества, по­зволяющие существенно приблизить средства обработки инфор­мации и управления к местам ее возникновения и приложения управляющих воздействий. В конструктивном отношении средства МП становятся встроенными, т. е. являются элементами и узлами автоматических систем, подчиненных своей логике, своим зада­чам.

Для дальнейшего развития систем управления технологически­ми объектами и процессами необходимо использовать CALS-тех-нологии. Это обеспечивает предоставление необходимой инфор­мации в нужное время, в нужном виде, в конкретном месте жиз­ненного цикла при изготовлении изделия. В этом случае задачами CALS-технологии являются структурирование и моделирование данных о технологических объектах; обеспечение эффективного управления и обмена данными; создание и сопровождение доку­ментации для поддержания жизненного цикла ТО.

Контрольные вопросы

1. Что является технологическим объектом в машиностроении?

2. Определите назначение систем управления ТО.

3. Что такое программа управления?

4. Что такое дискрета СУ?

5. Перечислите основные требования, предъявляемые к СУ.

6. По каким признакам можно классифицировать СУ?

7. Опишите принцип работы гидроусилителя.

8. Что такое статические и астатические СУ?

9. Какие преимущества имеют СУ с обратными связями по сравнению с СУ без обратных связей?

 

10. Определите назначение датчиков обратной связи.

11. Какие методы используют при формировании сигналов обратной связи?

12. В каких случаях используют шаговые двигатели и в каких — высоко-моментные двигатели?

13. Какие перспективы развития имеют СУ в условиях применения интегрированного автоматического управления?

Гла ва 7

ФОРМИРОВАНИЕ АВТОМАТИЗИРОВАННОГО

МАШИНОСТРОИТЕЛЬНОГО ПРОИЗВОДСТВА НА ОСНОВЕ

РАСПРЕДЕЛЕННЫХ ПРОИЗВОДСТВЕННЫХ СИСТЕМ

7.1. Принцип многообъектного технологического проектирования в распределенных производственных

системах

Процесс функционирования РПС характеризуется, в частно­сти, степенью загрузки технологического оборудования ее состав­ляющих. В реальных условиях при выполнении производственного задания (ПЗ) неизбежным является простой технологического обо­рудования, что можно объяснить следующими причинами: невоз­можностью подбора оборудования по технологическим возмож­ностям, однозначно соответствующим требованиям выполняемых ТП; неритмичностью прохождения плановых производственных за­даний; некоторым запасом по количеству и технологическим воз­можностям технологического оборудования с целью гарантиро­ванного обеспечения требуемых условий функционирования ПС и др. Все это приводит к появлению определенного объема избыточ­ности производственных ресурсов. Размер и состав ресурсов, а так­же характер их изменения во времени являются определяемыми параметрами ПС.

Процесс выполнения несколькими РПС своих ПЗ протекает обычно таким образом, что производственные процессы в них вы­полняются независимо один от другого. На рис. 7.1 представлена схема выполнения ПЗ в распределенных производственных систе­мах. Например, в /"-й РПС (1 < /< л) выполняется т, видов готовой продукции (ГП,). Для выполнения этого объема работ РПС,-дол­жна обладать технологической гибкостью, позволяющей реали­зовать соответствующие технологические процессы.

Технически возможная гибкость VS,-системы характе­ризует технически допустимые возможности переналадки систе­мы по отдельным рабочим параметрам (или их совокупности) и представляет собой зависимость вида

VS, = и KJvSijjc ,
J -\ \ k =\     J

где n_{Tj 0 i} — число единиц технологического оборудования в /'-и ПС; Qij — множество значений параметров j -к единицы технологичес­кого оборудования, достигаемые при ее переналадке; vs,-^ — уни­тарное значение параметра технических возможностей единицы оборудования.

271

П3,(/Л|)

РПС|

ГП|(т|)  Рис. 7.1. Прохождение производ­ственного задания через распреде-

П3₂(/я₂) _

РПС,

ГП2(т₂)  ленную производственную систему; П3|(/Я|), ..., П3,{/я„) — производствен-

............    ные задания; РПС„ .... РПС„ — распре-

2J3j(m/)_ |--- ргтр"------ i_ CU^"i?   деленные пронзиодственные системы;

**"!----------- J---- !       "*" ГП |(#П|),.... ГП„(/л„) — готовая продукция

ПЗ_л(т„) _

Н РПС„

ГП„(т„)_

Технологически необходимая гибкость VD,-системы характеризуется значениями изменяемых параметров, соответству­ющих значениям свойств сменяемых деталей:

VD, = и У=1

f^h '. j           ^

где vujjji — множество операций, необходимых для выполнения /и,-сменяемых деталей; йу — число операций, необходимых для полу­чения у-й готовой летали.

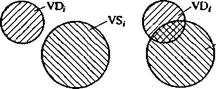
На рис. 7.2 приведены три варианта сочетаний технически воз­можной и технологически необходимой гибкости. На рис. 7.2, а отражен случай, когда рассматриваемую РПС нельзя использовать для выполнения заданного ТП даже частично. Здесь множество параметров технически возможной гибкости РПС, не имеет общей области с множеством параметров технологически необходимой гибкости, т.е.

VS, a VD_;.

Для случая на рис. 7.2, б показано, что РПС, можно использо­вать для выполнения лишь части заданного ТП, так как множе­ство технически возможной гибкости имеет обилую область с мно­жеством технологически необходимой гибкости:

VS,nVD,,

„vs.-

 

а                       б                      в

Рис. 7.2. Соотношение технически возможной гибкости VS и технологи­чески необходимой гибкости VD: а - VS, <z VD,; б - VS, n VD* e - VS, э VD,

272

На рис. 7.2, в представлен случай, когда средствами РПС,- мож­но полностью обеспечить выполнение заданного ТП. Множество технологически необходимой гибкости является подмножеством технически возможной гибкости:

VSjuVD,-.

В реальных ПС имеет место третий из приведенных случаев. Та­ким образом, каждую производственную систему можно рассмат­ривать как некоторый массив параметров, характеризующих ее технологические возможности, причем если одна часть этого мас­сива в каждый момент времени занята выполнением заданных ТП, то другая остается незагруженной. Причем по мере выполнения одних ТП и начала выполнения других соотношение этих частей будет изменяться как по своему составу, так и но размерам. При этом в каждый момент времени / можно представить совокупность свободных частей РПС как некоторую виртуальную производствен­ную систему, характерной особенностью которой является то, что она состоит из частей РПС, объединенных лишь организационно, без каких-либо материальных преобразований.

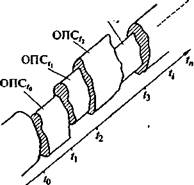
В любой период времени технологические возможности каждой РПС, в основном, связаны с выполнением некоторого объема ПЗ, на которые они ориентированы. При этом некоторая их часть ока­зывается свободной. Совокупность свободных частей РПС можно рассматривать как обобщенную ПС (ОПС), обладающую техноло­гическими возможностями, превышающими технологические воз­можности отдельных РПС. Такое объединение является условным, и информация об ОПС находится только в памяти ЭВМ. На рис. 7.3 представлен процесс формирования ОПС на основе свободных частей множества РПС.

Технологические возможности ОПС можно представить в сле­дующем виде:

где Kvsj — число одинаковых технологических операций, которые могут быть совмещены (1 < /' < п).

Мощность массива технологических возможностей ОПС изме­няется во времени. Это вызвано тем, что ЛЗ, поступающие в РПС, меняются и по номенклатуре, и объему партий. При этом соотно­шение занятых и свободных частей РПС также меняется. На рис. 7.4 показано изменение состояния ОПС, т.е. мощности массива тех­нологических возможностей, во времени.

На отрезках времени t ;- t - _nX (где / — произвольная величина) мощность массива технологических возможностей является посто­янной величиной. В некоторые моменты времени t_t очередная тех­нологическая операция завершается, далее в момент /_i4l, соответ-

273

ШШЁ

one

Рис. 7.3. Формирование обобщенной производственной системы на ос­нове свободных частей множеств РПС: заштрихованные области на РПС,, РПС₂, РПС,, РПС„ — свободные части РПС

ОПС.

Рис. 7.4. Изменение состояния обоб­щенной производственной системы во времени:

0ПС,_о,..., ОПС,_ — состояния обобщен­ной производственной системы в мо­менты времени /₀,..., /,,.... /„

274

ствующий началу следующей операции, мощность массива меня­ется скачкообразно.

В связи с определенностью сроков выполнения плановых зада­ний возможно определение параметров отдельных РПС, составля­ющих ОПС. Следовательно, с одной стороны, известно распре­деление технологических возможностей ОПС во времени, а с дру­гой — есть некоторый объем ПЗ, который должен быть выполнен. Производственное задание представляет собой задание на изго­товление конкретных видов изделий заданного количества.

Однотипные по составу технологического оборудования РПС увеличивают вторую составляющую параметра WO, а разнотип­ные РПС — первую. Параметр WO является комплексным, он ха­рактеризует технологические возможности ОПС.

Технологические возможности ОПС графически можно пред­ставить в виде слоев (рис. 7.5). Каждый слой характеризует физи­ческую привязку соответствующего множества технологических возможностей к конкретной РПС. Если маршрут обработки пред­полагает переход из одного слоя в другой, появляются дополни­тельные затраты Q \, связанные с транспортировкой изделия на этапе его изготовления:

где 9_Ш1утр — затраты на транспортировку изделия в процессе его изготовления в пределах одной РПС; <у_Внсшн * затраты на транс портировку изделия в процессе его изготовления при перемеще­нии из одной РПС в другую.

Технологические возможности РПС

Рис. 7.5. Распределение слоев 1 —и в обобщенной производственной системе: РПС — распределенная производственная система

275

Целью формирования ПС является выполнение ПЗ в заданные сроки при минимальной себестоимости. С этой целью необходимо

оптимизировать объем технологических возможностей, задейство­ванных для его выполнения. При этом суммарные затраты (?_х на выполнение каждого ПЗ должны быть минимальны:

*.<2, + К₂<2₂+К₃<2_ъ = тю<2ь,

где C?i — затраты на транспортировку изделия в процессе его изго­товления; Q ₂ — затраты на обработку при изготовлении изделия; (?з — затраты на штрафы, предусмотренные при нарушении сроков выполнения ПЗ; К\, К₂, Лз — коэффициенты значимости затрат.

Для выполнения ПЗ требуется использование части ресурсов ОПС, следовательно, на основе ОПС необходимо с(}юрмировать ПС, наилучшим образом отвечающую требованиям обеспечения выполнения ПЗ. Поскольку информация об организации такой ПС содержится только в памяти ЭВМ, то система является виртуаль­ной производственной системой.

При формировании ВПС необходимо выполнить следующие условия:

1. Минимизировать объем используемых ресурсов, необходимых для выполнения ПЗ;

2. Максимизировать положительный результат, который можно получить с имеющимся запасом ресурсов;

3. Получить наилучший баланс затрат (используемых ресурсов) и результатов (выполнения ПЗ).

Время жизни конкретной конфигурации ВПС определяется, с од­ной стороны, требованиями текущего ТП, с другой — ресурсами ОПС, определяемыми возможностями каждой РПС с точки зре­ния их собственной загрузки текущими ТП.

Процесс формирования ВПС характеризуется распределением ресурсов ОПС во времени и построением ТП для выполнения ПЗ. Поскольку ПЗ состоит из нескольких видов изделий, процесс про­ектирования ТП по изготовлению каждого из них будет опреде­ляться результатами проектирования ТП по изготовлению других видов. Таким образом, процессы проектирования ТП всего ПЗ ока­зываются взаимосвязанными и зависящими один от другого, что определяет многообъектность технологического проектирования в условиях ВПС. Процесс технологического проектирования в ВПС определяется следующими параметрами: распределением произ­водственных ресурсов ОПС, характеристиками каждого наимено­вания изделий, количеством изделий каждого наименования, сро­ками их выполнения.

Формирование очередной конфигурации ВПС определяется вза­имодействием двух информационных потоков: об изготавливаемых изделиях и о параметрах ОПС. Управление процессами взаимодей­ствия отдельных частей ОПС при формировании ВПС обеспечива­ет выполнение заданных ПЗ при минимальных экономических зат­ратах.

276

Под управлением будем понимать формирование командной информации на основе принятия решений по комплексной про­блеме распределения ресурсов и использования технологий. Ос­новной особенностью такого управления является во многих случа­ях предварительное принятие решений, так как достижение же­лаемого состояния ВПС зависит от набора взаимосвязанных ре­шений (системы решений). Другая особенность заключается в том, что решения, принятые на ранних этапах процесса управления, должны приниматься с учетом их влияния на последующие ре­шения.

Это управление связано, с одной стороны, с предотвращением ошибочных действий за счет выявления таковых на ранних этапах и, с другой, с уменьшением объема неиспользованных возможно­стей существующих ПС. Большое число параметров, влияющих на процесс принятия решения, и большой объем вычислений при моделировании повеления ВПС во времени, а также ограничен­ность времени требуют построения СУ на основе интеллектуаль­ного управления. Интеллектуальное управление позволяет в усло­виях ограничения времени частично, а в ряде случаев и полнос­тью заменять функции человека на стадиях подготовки исходной информации, моделирования, анализа полученной информации и формирования командной информации.

7.2. Разработка инвариантной информационной модели виртуальной производственной системы

Технологическое проектирование в условиях РПС является мно­гоэтапным и итерационным. При таком проектировании необхо­димо формирование информации, включающей в себя массивы данных о предметной области, существующих и разрабатываемых структурах объекта, известных и прогнозируемых отношениях и связях между элементами и свойствами объекта и внешней средой. Такая информационная среда представляет собой порождающую среду, необходимую для принятия решений, на основе которых осуществляется оперативное управление. Составными частями этого управления являются технологическое и организационное управ­ления. Цель технологического управления — обеспечение требуе­мых свойств изделия, цель организационного управления — фор­мирование ВПС для реализации ТП, необходимых для выполне­ния ПЗ. Эти управления осуществляют динамическую перекомпо­новку ресурсов отдельных доступных частей РПС.

Следует отметить, что решаемая проблема осложняется огра­ниченностью во времени процессов принятия решения и частым изменением как состава ресурсов доступных производственных систем, так и их параметров.

277

БД

Проектирование ТП

ВПС

Моделирование процесса

 

ипз

© ■

е

Интеллектуальное

управление технологическим проектированием

Менеджер

" ТТ "

Готовые изделия

Рис. 7.6. Схема формирования виртуальной производственной системы:

БД — база данных; БЗ — база знаний; ПЗ — производственное задание; ИПЗ —

информация о производственном задании; ТП — технологический процесс; ВПС —

виртуальная производственная система; ОПС— обобщенная производственная

система; РПС — распределенная производственная система

Для выполнения ПЗ требуется спроектировать ТП и для реали­зации данных процессов сформировать ВПС на основе ОПС. Схема формирования ВПС на основе ОПС представлена на рис. 7.6. Ин­формация о ПЗ поступает в систему технологического проектиро­вания с интеллектуальным управлением. Здесь осуществляется ана­лиз поступающей информации, на основе которого принимаются решения по вопросам выбора текущей конфигурации ВПС, оп­ределения маршрутов ТП и формируется командная информация для менеджера и РПС, составляющих ВПС.

Анализ и принятие решений осуществляются на основе инфор­мации о технологических возможностях ОПС, их распределении во времени, информации о ПЗ в виде спроектированных на них ТП. При этом используются базы данных (БД) и базы знаний (БЗ).

Система управления производством на основе получаемой ин­формации о характеристиках ПЗ и информации об ОПС определя­ет стратегию ТП, включающую в себя проектирование ТП, рас­пределение выполняемых технологических операций непосред­ственно по технологическому оборудованию и последовательность запуска ПЗ.

* 278

Качество функционирования ВПС определяется ее свойствами, основными из которых являются: живучесть, прогнозируемость, устойчивость, управляемость, наблюдаемость.

Для обеспечения надежного функционирования ВПС требуется обеспечение независимости ее функционирования от воздействий внешней среды. Для систем, построенных по иерархической струк­туре, характерна живучесть — свойство активно противостоять вредным воздействиям внешней среды и выполнять свои функции в условиях такого воздействия. Благодаря этому свойству отказ ка­кой-либо подсистемы приводит не к отказу всей системы, а только к некоторому снижению эффективности ее функционирования.

Использование в ВПС параллельного функционирования род­ственных элементов или элементов одинакового назначения обес­печивает живучесть системы, т.е. ее функционирование, но с мень­шей эффективностью, при выходе из строя одного или несколь­ких элементов. Работа по такому принципу получила название «фун­кционирование с горячим резервом». Применительно к ПС в усло­виях многопоточной обработки выход из строя одного или несколь­ких единиц технологического оборудования не приводит к оста­новке всей системы; ее работа продолжается, однако с более низ­кой производительностью и, как правило, с измененным алго­ритмом управления.

Функционирование ВПС основывается на моделировании про­текающих производственных процессов. Состояние ее параметров определяется для отдельных моментов времени (,. При моделирова­нии ВПС на последующих интервалах времени вследствие воздей­ствия вредных факторов могут возникнуть ситуации, когда резуль­тат оказывается недопустимо отличным от реальных параметров.

Причиной возникновения подобной ситуации являются ошибки при формировании исходной информации, непредсказуемые, вне­запные изменения состояния РПС или их элементов, задействован­ных в ВПС, и т.д. (например, внезапный отказ какого-либо техноло­гического оборудования). Поэтому функционирование системы мно­гообъектного технологического проектирования должно быть защи­щено от сбоев, что достигается резервированием и архивацией (фик­сированием) промежуточных состояний системы проектирования.

При сбое системы ее восстановление осуществляется с пара­метрами последней архивации. Для этого предусмотрен реестр Н~, куда регулярно заносится информация о промежуточных резуль­татах работы системы:

н - _п

279

где Hf — i'-й параметр, полученный в системе проектирования на последнем шаге функционирования.

Кроме того, в реестр заносится информация о получаемых па­раметрах на различных шагах (информация о предыстории функ­ционирования ВПС). Такая организация позволяет не только пе­рейти к последнему состоянию системы, но при необходимости вернуть ее в более раннее состояние. Это может оказаться необхо­димым при получении отрицательных результатов в случае непра­вильной организации действий системы на некотором шаге.

Таким образом, восстановление системы оказывается возмож­ным до состояния, предшествующего моменту времени приня­тия «неправильного» решения. Тем самым возможно исправление ошибки.

Прогнозируемость ВПС обеспечивается, прежде всего, на­личием адекватных ММ ее составляющих элементов и моделиро­ванием процесса ее функционирования во времени. Одним из ос­новных условий обеспечения точности прогноза является своевре­менное получение достоверной информации об изменении ситуа­ции и соответствующей коррекции параметров модели на прогно­зируемый период времени.

Устойчивость ВПС определяется наличием ОС и нелиней­ностью ее характеристик (элементы оптимального управления). Наличие информации из ОС позволяет осуществлять регулярное сопоставление текущих параметров элементов РПС, составляю­щих ВПС, и параметров, полученных для этого этапа с помощью модели. При неадекватности полученных данных оперативно вы­рабатывается командная информация на коррекцию параметров модели и учет факторов, вызвавших это различие.

Управляемость ВПС может трактоваться как задача пере­вода системы из одного заданного состояния в другое за конечное время. Система будет управляемой, если для любых моментов вре­мени /₀ и /| выполняется условие /| > /₀ и для любых заданных состояний z₀ и Z \ существует управление (7(/) на интервале време­ни t ₀ < t < /,, переводящее начальное состояние Z(/₀) = z₀ в конеч­ное Z ( t_t ) = г,.

В связи с тем, что формирование РПС происходит при выпол­нении условия обеспечения возможности управления любым па­раметром состояния элементов РПС, составляющих ВПС, рассмат­риваемая система является полностью управляемой.

Наблюдаемость ВПС является важным свойством системы при ее управлении. Для осуществления управления (независимо от того, выполняется оно автоматически или вручную) необходимо иметь информацию о текущем состоянии системы, т.е. о значени­ях переменных состояния х в каждый момент времени. Однако не­которые из переменных z_t являются абстрактными переменными, не имеют физического аналога в реальной системе и поэтому не

280

могут быть измерены. Измеряемыми и наблюдаемыми в системе являются выходные переменные Н, через которые должны одно­значно выражаться все составляющие вектора состояния Z .

Выходную переменную //можно определить следующим образом:

Я = WZ , где W — матрица

w_u w_n ... и>,_; ... и/,„ w_n w₂₂ ... w_2i ... w_2n

W_nq  W „₂  ... W „;  ...  W „„

Переменная Я будет наблюдаемой, если матрица W не содер­жит столбцов, элементы которых равны нулю.

В качестве исходных данных при моделировании процессов фун­кционирования ВПС могут быть следующие показатели:

1) продолжительность жизненного цикла ВПС;

2) прогнозное значение периода времени, в течение которого достоверность информации, получаемой в результате моделирова­ния, отвечает заданным условиям;

3) ограничения (желательные уровни), определяющие соответ­ствие процесса функционирования ВПС заданным условиям;

4) данные по каждой доступной ПС (ресурсы, продолжитель­ность доступа, сроки доступа).

При проектировании ТП в условиях РПС необходимо учиты­вать состав ПЗ. Совокупность работ (включая проектные), необхо­димых для изготовления некоторого вила (номенклатуры) изде­лий, составляющих ПЗ, рассматривают как отдельный проект.

Под жизненным циклом проекта понимают часть пе­риода жизненного цикла изделия от момента формирования тех­нического задания на проектирование и до момента окончания его изготовления. ПЗ, поступающие в ВПС, можно подразделить на две группы: независимые и зависимые одно от другого.

К группе независимых ПЗ относят изделия, ТЗ, на которые не зависят от результатов процесса проектирования других изделий. Период жизненного цикла проекта

т — т   + т

* ж.ц ~~ ^л проект! ' ' иэготэ

где Т_{ж ц} — период жизненного цикла проекта; T_{np ( XKT} i — время про­ектирования изделия; Г_изгот — время изготовления изделия.

К категории зависимых относят изделия, ТЗ на которые зависят от процесса проектирования других изделий. В этом случае для про­цесса проектирования требуются данные, которые могут быть сфор­мированы только на основании информации, полученной в про-

281

цессе проектирования других изделий (являющейся, например, базовой относительно рассматриваемого).

В этом случае период жизненного цикла проекта

^гД^е ^просктг — время проектирования производственно связанного изделия.

Информацию об отдельных характеристиках технологического оборудования (оснастка, инструмент, станки и т.д.) можно пред­ставить в виде отдельных векторов. Совокупность векторов, пред­ставляющих собой отдельные виды информации по отдельным составляющим ПС, можно выразить в виде вектора X ориентации системы на выпуск некоторого вида изделий:

X = | Х\, х₂, х$,..., ж,-1,

где Х| — вектор целевого назначения технологического оборудо­вания ПС; х₂ — вектор целевого назначения инструмента ПС; х₃ — вектор целевого назначения приспособлений ПС; х, — век­тор отдельных видов технологической оснастки составляющих ПС. О том, насколько данная ПС соответствует по возможностям производству конкретного изделия, можно судить по вектору А:

Л = ХхУ,

где Y — вектор необходимой технологической ориентации на вы­пуск рассматриваемого изделия.

Формирование ВПС начинают с определения ее структуры. Структурное моделирование является наиболее сложной областью для формализации. В большинстве систем автоматизированного про­ектирования основные функции структурного моделирования вы­полняет человек. Выполнение этих функций может осуществлять­ся как в процессе проектирования, так и при описании предмет­ной области. При автоматизированном проектировании объекта вначале формируется порождающая среда, в которой будет осу­ществляться синтез этого объекта. Порождающая среда включает данные о предметной области, к которой относится объект, о су­ществующих и разрабатываемых структурах объекта, известные или прогнозируемые отношения и связи между элементами и свой­ствами объекта и внешней среды. Возможность получения в ре­зультате моделирования нескольких вариантов структур позволяет менять состав элементов структуры в зависимости от изменения внешних условий. Такими условиями могут быть: 1) параметры ПЗ; 2) наследование свойств ТП от результатов предшествующего проектирования подобных ТП; 3) изменение значений парамет­ров ПС; 4) диалоговая корректировка результатов проектирова­ния пользователем на основе анализа текущих требований техно­логического проектирования.

282

Информацию о свободных частях РПС можно представить в двух вариантах данных:

• о конкретном технологическом оборудовании РПС и сроках его возможного использования;

• о конечном результате выполнения ПЗ или его части.

В первом случае информация о свободных частях РПС представ­ляется в виде исходных данных о свободном технологическом обо­рудовании, на основе которых формируется ОПС. Далее осуществ­ляют технологическое проектирование и реализацию спроектиро­ванных ТП d сформированной ВПС.

Во втором случае сразу представляется информация о конеч­ном результате реализации заданного ПЗ или его части в некото­рой РПС без указания ее характеристик. В этом случае такую РПС можно рассматривать как «черный ящик», в котором осуществля­ется ТП в оговоренные сроки при установленных условиях.

7.3. Информационные обратные связи в виртуальной производственной системе

Для высокоэффективных ТП наряду с оборудованием, выпол­ненным с высоким качеством, требуется управление, которое обес­печивает оптимальное по всем параметрам протекание процесса. Для этого необходимо выполнение следующего условия:

F ( X , Х\ ...; U , U \ ...) = С(Л/,-Л/', ...; L , Г, ...),

где F ~ функция, определяющая текущие значения параметров X , Л",..., U , V , ... протекания конкретного технологического про­цесса; С — целевая функция оптимального сочетания отдельных параметров технологического процесса в каждый момент време­ни, при которых наилучшим образом обеспечивается его протека­ние.

Рахчичают два случая формирования исходной информации:

• текущие оптимальные значения параметров технологического процесса известны;

• текущие оптимальные значения параметров неизвестны, из­вестны лишь конечные значения параметров или закон изменения некоторого конечного числа параметров.

Стратегию обеспечения протекания ТП с высоким качеством можно представить целевой функцией

X 6,(/)= i ( G _/ (/)- n ( o )_>

где 8,(0 — текущее значение функции рассогласования для /-го параметра; (?;(/), Yj ( t ) — текущие значения соответственно функ­ций входного и выходного /-го параметра.

При оптимальном протекании ТП указанная целевая функция стремится к нулю. Целевая функция включает в себя многомерную информацию по каждому параметру, о его производных и одно­временно носит распределенный характер, определяющийся раз­личным физическим смыслом параметров, влияющих на протека­ние технологического процесса.

Для /-го выходного параметра можно записать выражение

£*„,

Up) = G,(p)

t kjvxp)

ТО =]

Q №(p)£K_m+Qi"~-^x

m=l

где W ,{ p ) — передаточная функция технологической системы по /'-му параметру без учета действия обратной связи; К_т — коэффи­циент погрешности звеньев технологической системы, охвачен­ных обратной связью; К„ — коэффициент погрешности звеньев технологической системы, не охваченных обратной связью; Q_t — погрешность измерительного преобразователя информации обрат­ной связи; j , I — обшее количество параметров технологической системы.

С учетом теоремы о конечном значении можно преобразовать последнее выражение следующим образом:

Up) = iim(o,)

Р -»0

KJV;{P)

 

т=\

Т.к.

" ^аАр) "⁼оГ

Полученное выражение справедливо для астатических систем по t-му управляющему воздействию, что обычно обеспечивается соответствующей организацией управления. На основе получен­ной формулы можно записать следующее выражение для отклоне­ния текущего 1-го параметра:

8, = а,

я-1

Qi

из которого следует, что в статическом режиме величину отклоне­ния определяют конечной точностью ММ. В динамическом режи­ме отклонения параметров будут определяться дополнительными динамическими ошибками, возникающими при реализации во времени управляющих воздействий в ВПС. Уменьшить указанные ошибки можно путем сравнения управляющей информации об

284

изменениях управляющего воздействия и информации о реальной отработке этих изменений.

Процесс функционирования ВПС определяется результатами моделирования протекания ТП в ней. Ввиду неполной адекватно­сти ММ реальной ПС результаты моделирования могут существенно отличаться от реального состояния ПС. При получении информа­ции о параметрах РПС могут возникать ошибки в информацион­ном обеспечении, обусловленные следующими причинами:

• ошибки в определении параметров РПС (изменение состава и параметров технологической оснастки, динамическое изменение параметров элементов ПС);

• непредсказуемые изменения характеристик РПС (внезапный выход из строя отдельных технологических единиц оборудования, отказ отдельных ПС при выполнении своей части работ и др.).

Коррекция параметров модели с целью уменьшения расхожде­ния результатов моделирования и параметров ПС обеспечивается введением обратной связи (ОС).

Информация ОС представляет собой обратный информацион­ный поток, который позволяет сопоставить информацию, полу­чаемую в результате моделирования, и информацию о реальном функционировании частей РПС, составляющих ВПС. На рис. 7.7 представлена структура ОС в ВПС.

Достоверность информации о параметрах технологического обору­дования в РПС обеспечивается передачей данных, получаемых в ре­зультате диагностирования в них технологического оборудования. Кро­ме того, должно проводиться периодическое обследование техноло­гической оснастки на предмет снижения трудоемкости переналадки и получения информации о затратах времени на эту переналадку.

Информация о реальных сроках выполнения ПЗ необходима для коррекции результатов моделирования и формирования информа­ции у.транления. В случае изменения реальных сроков выполнения ПЗ осуществляется коррекция исходных данных ММ функциони­рования ВПС и далее проводится расчет с учетом их новых значе-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Информация обОПС

Форми­рование ВПС

—>*•

Принятое решений и выработка информации управления

—»-

РПС

Проектирование технологических процессов

Информация оПЗ

■*

i

,

,

,

,

.

|

1_

Рис. 7.7. Структура обратной связи в виртуальной производственной системе

285

ний. В этом случае может возникнуть необходимость возврата значе­ний состояния модели к значениям более раннего момента времени. В случае принятия решения по коррекции процесса функцио­нирования ВПС возможны следующие варианты:

1) корректировка размеров заготовки;

2) изменение маршрута обработки;

3) совершенствование и уточнение ТП;

4) корректировка процесса запуска ПЗ на выполнение;

5) выбор других точек ВПС, в которых осуществляется за­пуск ПЗ;

6) модификация текущей конфигурации ВПС;

7) конструкторская доработка технологической оснастки, из­менение операционной технологии, оснащение станков легкопе-реналаж»гоаемой широкодиапазонной технологической оснасткой, обеспечивающей без значительной переналадки высокоточное ба­зирование и надежное закрепление заготовки в процессе обработки;

8) корректировка конструкции детали.

Использование промежуточной информации о выполняемых ТП на этапах моделирования позволяет проводить ориентировочные экономические расчеты технико-экономической эффективности. На основе этих расчетов оказывается возможным на ранних этапах жизненного цикла изделия получить данные о его себестоимости и условиях производства, строить оптимальные ТП применитель­но к конкретным производственным условиям.

Получение информации ОС осуществляется следующими путями:

• промежуточная оценка проектируемых вариантов с помощью
экономических расчетов;

• обследование элементов ПС (получение и уточнение параметров).
Наличие ОС в ВПС позволяет рассматривать ее как замкнутую

систему. Алгоритм управления увязывается с алгоритмом функци­онирования системы и ее фактическим состоянием. Для этого осу­ществляются определение текущих значений выходных перемен­ных N ( t ), их сравнение с заданным G ( t ) и выработка управляю­щих воздействий £(/) на входы системы в зависимости от текуще­го отклонения ( G - Н). В системе переменные £"уже не являются внешними воздействиями, не зависящими от выходных перемен­ных. По существу, они должны рассматриваться как часть выход­ных переменных. К внешним воздействиям в данном случае можно отнести компоненты вектора //(/).

7.4. Методы и средства моделирования процесса формирования виртуальной производственной системы

Особенностью автоматизации процесса формирования ВПС яв­ляется отражение его в ММ. Под ММ ВПС будем понимать систе-

286

му математических соотношений, описывающих с требуемой точ­ностью элементы РПС и процессы их взаимодействия, их поведе­ние в реальных условиях.

Математические модели элементов РПС, входящих в ОПС, представляют собой модели большой размерности, в которых дол­жны учитываться ограничения и условия, во многих случаях не поддающиеся прямому аналитическому описанию. Вследствие этого такие модели часто невозможно представить в виде аналитических моделей. Поэтому при разработке ММ процессов формирования ВПС используют имитационное моделирование, которое наряду с другими методами составляет комплексную процедуру.

При имитационном моделировании применяют прямое описание моделируемых объектов. Такие модели характеризуются структурным подобием объекта и его модели. При имитационном моделировании проводят имитационный эксперимент, реализуемый с помощью ЭВМ. При этом ММ отражает поведение моделируемого объекта при заданных, меняющихся во времени, внешних воздействиях.

Имитационное моделирование осуществляется путем воспро­изведения событий, происходящих одновременно или последова­тельно в модельном времени. При этом под событием понимается факт изменения любой фазовой переменной.

Основное назначение имитационного моделирования состоит в выделении наиболее существенных переменных, оценке степе­ни их влияния на исследуемые параметры, изучении воздейстпия различных организационных, управленческих и технико-экономи­ческих изменений на показатели функционирования ПС и ее эле­ментов. На основе этой информации проводят оценку получаемых решений при поиске оптимальной структуры ТП и рациональной структуры ПС, реачизующей этот технологический процесс.

В имитационных моделях зависимость выходных параметров от внутренних и внешних воздействий задается неявно в виде алго­ритма моделирования, который отражает процессы в системе при наличии внешних воздействий на нее. Таким образом, имитацион­ная модель является алгоритмической поведенческой моделью.

В качестве составных частей имитационной модели используют аналитические ММ, описывающие отдельные явления в общем про­цессе функционирования ВПС. На основе аналитических ММ осу­ществляются процедуры оптимизации, посредством которых про­водится поиск лучших вариантов условий функционирования ВПС.

Аналитическое моделирование целесообразно использовать в имитационных моделях, так как для него не требуются значитель­ные затраты вычислительных ресурсов. Часто без постановки спе­циальных вычислительных экспериментов разработчик может оце­нить характер влияния аргументов на выходные параметры, опре­делить их оптимальные или рациональные значения. Как правило, аналитическое моделирование реализуется в отдельных частных

287

сравнительно несложных процессах, имеющих место при техно­логическом проектировании.

Одним из важнейших разделов математической теории управле­ния и планирования является линейное программирование. Методы линейного программирования позволяют решать оптимизационные задачи распределения ресурсов и минимизации затрат. Задачи тако­го рода возникают при планировании загрузки технологического оборудования В ПС, разработке методов управления в ней и плани­ровании последовательности запуска отдельных составляющих ПЗ.

Задача линейного программирования формулируется следую­щим образом. Требуется определить экстремум некоторой целевой функции L ( X ) переменных Х = (х_1г ..., х„):

п

ЦХ) = Цх_и ...,х„) = Хс,х, -> max, 1=1

где Cj — коэффициенты, при следующих ограничениях, наложен­ных на переменные (запись в векторной форме):

Я                                                                  

Yj Л*, ^ В, х,- > О, I = 1, п, j - 1, т,

где А, =

— /-и вектор-столбец условий задачи; В -

вектор-столбец ограничений задачи.

Векторы Aj в совокупности образуют матрицу А = | а$\ условий задачи. Если хотя бы один из коэффициентов с, равен нулю, то целевая функция не ограничена в пространстве X , т.е. ввиду этого задача о максимуме такой функции без ограничений смысла не имеет.

Другие варианты задач с линейной целевой функцией Р_и и ли­нейными условиями dj можно записать в иных формах.

л

1. Неравенство Х^/,_ух,- - ^ h ГДех,— параметры системы, мож-
но привести к форме (8.9), изменив знак обеих его частей:

t - P_ijXi >- dj ы

и обозначив a , j = -Р,у, bj = - dj .

п

2. Условие в форме равенства ^ Р, jX / = dj можно переписать в

;= » виде двух следующих неравенств:

/= i                        i = i

288

3. Условие y_f > d -, после введения замены

Xi- yi- d, можно привести к виду

Xj > 0.

4. Замену задачи на минимум задачей на максимум можно вы­
полнить при изменении знака L .

Сложность решения задач линейного программирования состо­ит в том, что прямой путь решения — построение системы воз­можных вариантов и выделение из них оптимального — практи­чески неосуществим при увеличении числа переменных х,- (с уве­личением 0, так как в этом случае возникает необходимость про­ведения большого числа операций, что приводит к недопустимо большим затратам машинного времени даже с учетом использова­ния современных быстродействующих ЭВМ. Поэтому в каждом конкретном случае необходимо рассматривать возможность при­менения тех или иных методов линейного программирования, ис­ходя из размерности конкретной задачи.

На начальных этапах технологического проектирования часто используют метод динамического программирования. Для каждого ПЗ определяют оптимальный маршрут его прохождения по отдель­ным рабочим местам без учета влияния других ПЗ. При этом затра­ты на возможную первую операцию составят

Г, =/(Г,).

Затраты на вторую операцию

T ₂ = f ( T ₂ ) + Т_и

нау'-ю операцию

7} = /(7])+ 7J.„

где у — число технологических операций. Функция

Л(Г„7'₂,...,Г₁,) = Х*(⁷'Д

j =\

где р — общее число операций, является целевой и определяется длительностью производственного процесса по одной конкретной изготовляемой детали. Соответственно функция

G = g<r„7'j,...,7',)

является функцией стратегии. Стратегия, максимизирующая фун­кцию R , является оптимальной стратегией.

ЮЗак.519

289

Тогда из принципа оптимальности для любого начального ре­шения j = 1

g ( T_x ) + [ g ( T ₂ ) + ... + g ( T_p )] = *(71) + FjMCTt )].

Отсюда получаем основное рекуррентное соотношение

Д(П = 1Ип[я(Г₁) + /^₁1ЯГ₁)1,

которое позволяет из нескольких возможных вариантов выполне­ния ТП, заданных с помощью структурной модели, выбрать опти­мальный вариант на основе анализа с помошью целевой функции. Реализация используемых математических методов ввиду их высо­кой трудоемкости должка осуществляться средствами автоматизи­рованного комплекса.

Автоматизированный комплекс строится в рамках интегриро­ванной программно-аппаратной среды интегральной проектно-производственной системы или как автономное образование соот­ветствующих подразделений на основе интеграции программного обеспечения, технологического обеспечения и средств обеспече­ния качества технологических процессов и изделий с использова­нием средств вычислительной техники.

7.5. Особенности технологического проектирования в виртуальной производственной системе

Технологическое проектирование в условиях РПС предполагает выполнение следующих условий:

• минимальная себестоимость выполняемых ТП;

• рациональное распределение во времени моментов запуска отдельных ПЗ на выполнение;

• выполнение заданных сроков выполнения ПЗ.

Большой объем технологических возможностей ОПС, превы­шающий объем требуемых по условиям выполнений ПЗ, позволя­ет осуществлять формирование различных приемлемых вариантов конфигураций ВПС. Каждая из этих конфигураций по-разному использует ресурсы ОПС при выполнении одних и тех же ПЗ. На рис. 7.8 представлен график распределения зон используемых ре­сурсов ОПС во времени.

С увеличением объема ресурсов ОПС, используемых в ВПС, сроки выполнения всего объема ПЗ сокращаются. Оптимальным объемом используемых ресурсов следует считать такой, при кото­ром сроки выполнения ПЗ совпадают с заданными.

В реальных условиях рациональным оказывается использование в ВПС объема ресурсов ОПС, при котором сроки выполнения ПЗ оказываются более короткими относительно заданных. В этом слу­чае при возникновении непредвиденных изменений параметров

290

С о -

2

_/

Рис. 7.8. Распределение зон используе­мых ресурсов обобщенной производ­ственной системы во времени:

/ — время; / — зона недопустимого распре­деления ресурсов ВПС; 2 — зона допусти­мого распределения ресурсов ОПС; 3— зона рационального распределения ресурсов ОПС; 4 — зона недопустимого распределе­ния ресурсов ОПС; 5 — зона оптимального распределения ресурсов ОПС

РПС и (или) вследствие ограниченной точности используемых ММ исключаются срывы заданных сроков выполнения ПЗ.

Зона рационального распределения ресурсов ОПС в ВПС опре­деляется конкретными производственными условиями и вероят­ностью возникновения случайных событий, влияющих на проте­кание производственных процессов. С целью снижения влияния случайных факторов на процесс выполнения ПЗ в некоторых слу­чаях оказывается целесообразным формирование группы элемен­тов ПЗ на базе основного задания (элементы ПЗ с «короткими» сроками) и части вспомогательного (элементы ПЗ с «длинными» сроками), требующего выполнения той же технологической опе­рации. Тогда влияние случайных факторов оказывает воздействие на ход выполнения вспомогательных ПЗ, а основное ПЗ выполня­ется в расчетные сроки.

Проектирование ТП в условиях РПС d первую очередь предпо­лагает синтез его структуры. Под структурой ТП будем понимать частично упорядоченную последовательность технологических ус-тановов, обеспечивающих весь процесс изготовления изделия, т. е. порядок обработки поверхностей с указанием соответствующих технологических баз. Процесс структурного синтеза определяется степенью сложности изготовляемого изделия. Целью такого про­цесса является получение оптимального технологического марш­рута изготовления детали, при котором достигается максимальная производительность (при обеспечении выполнения прочих задан­ных условий, например, себестоимости, точности и т.д.).

Частичная упорядоченность заключается в том, что некоторые установы могут объединяться в одной технологической операции, исходя из общности применяемого оборудования и схем базиро­вания. В общем случае это синтез структуры ТП, определение со­става его элементов, технологических связей между ними (топо­логии) и средств технической реализации (состав технологического

10*

291

оснащения). Порядок обработки поверхностей устанавливается в результате анализа выполнения различных действий в текущей проектной ситуации, соответствующей конкретной стадии изго­товления детали, и определения возможных будущих ситуаций.

На основании полученного порядка обработки поверхностей строится схема ТП и осуществляется анализ соблюдения величин допусков на вьтолняемые размеры, рассчитываются припуски на обработку (с проверкой соответствия их величин выбранным ме­тодам обработки) и операционные размеры, выбирается техноло­гическое оборудование. При удовлетворительных результатах ана­лиза полученное проектное решение принимается, в противном случае после корректировки исходной гипотезы, например, вве­дением дополнительной обработки некоторых поверхностей, син­тезируется новый вариант структуры. В заключение окончательно формируются технологические операции при объединении соот­ветствующих установов.

Таким образом, процесс выработки варианта проектного реше­ния состоит из последовательных действий по выдвижению взаимо­исключающих альтернатив, их оценке и собственно выбору. Задача решается одновременно на двух уровнях: выдвижение гипотезы решения задачи и подтверждение этой гипотезы. Синтез лучшего в некотором смысле варианта структуры или первого работоспособ­ного варианта осуществляется методом перебора. При этом пере­бор является некомбинаторным, т. е. проверяются не все возмож­ные альтернативные варианты, а осуществляется направленный поиск с исключением из рассмотрения заведомо неприемлемых решений. Это достигается за счет использования общих знаний проблемной среды и «внутренней» модели проблемной ситуации. На основании информации, которая содержится в размерно-точ­ностных отношениях, конструктивно-геометрических свойствах детали на разных стадиях ее обработки и эвристических методах, осуществляется анализ полученных результатов. На основе прове­денного анализа исключаются заранее неприемлемые варианты и сужается пространство поиска. При этом решение находится за меньшее число шагов, чем потребовалось бы при полном переборе.

В условиях ВПС процесс структурного синтеза является много­вариантным, что необходимо для оперативной адаптации ТП под ее текущую конфигурацию. Результатом процесса проектирования могут быть несколько рабочих вариантов реализации одного и того же ТП, число таких вариантов зависит от сложности изготовляе­мой детали. При проектировании создается очередной вариант од­ного и того же ТП, далее выполняется проверка на работоспособ­ность этого варианта с помощью целевой функции. В случае несо­ответствия спроектированного варианта осуществляется анализ причин несоответствия и принимается решение по изменению этого варианта в желательном направлении.

292

В самом элементарном случае, когда изготовляемое изделие по своей конструкции является достаточно простым, как правило, структура ТП или его элементов (операции, переходы) уже зада­ны. В этом случае используют таблицы применяемости.

При более сложных конструкциях изготовляемых изделий гене­рируется набор вариантов маршрутов, из которых путем перебора вариантов счетного множества выбирается рациональный (не все­гда оптимальный). При переборе каждая проба включает в себя поиск (создание) очередного варианта, принятие решения о за­мене ранее выбранного варианта последующим и о продолжении или прекращении поиска новых вариантов. Для полного перебора вариантной структуры из конечного множества необходимо зада­вать все элементы множества. Такой перечень имеет вид каталога типовых вариантов структуры (маршрутов обработки) в виде БД.

Когда вследствие сложности изготавливаемых деталей число вариантов структур ТП оказывается достаточно большим, при ре­шении задачи структурного синтеза исходят из практики исполь­зования промышленного опыта, знаний технолога и экспертных оценок. В этих случаях целесообразно формирование модели экс­перта, которая включает формализованную совокупность сведе­ний, в частности, о построении маршрутов обработки, выборе технологического оборудования, режущего инструмента, данные о применении технологии размерной обработки, закономернос­тей процессов обработки и правила использования в задаваемых ситуациях этих данных для принятия новых решений.

При устоявшейся номенклатуре изготовляемых деталей при синтезе структуры ТП (маршрута, операции) исходной информа­цией являются группы (подгруппы) изготовляемых деталей. Со­здается БЗ (модель эксперта), включающая правила создания обоб­щенной структуры маршрутов операций (переходов), причем мар­шруты выполняемых операций (переходов) имеют типовую пос­ледовательность и содержание.

В тех случаях, когда номенклатура изготовляемых деталей неус­тоявшаяся, исходную информацию целесообразно представлять в виде базового (типового) конструктива (конструктивов), изготов­ляемого комплекта деталей и конструктивного обогащения (от­дельных конструктивных элементов). Таким образом, процесс из­готовления комплекта деталей можно представить как совокуп-носгь ТП на базовые конструктивы и переходов на обработку эле­ментов конструктивного обогащения. Такой подход позволяет пе­рейти к блочно-модульному принципу проектирования ТП и под­готовки управляющих программ для станков с Ч ПУ. Модель экс­перта включает правила, учитывающие соотношение конструктив­ных признаков базового типового образа (конструктива) и конст­руктивных элементов обогащения, что определяет проектирова­ние типового или единичного ТП.

293

Синтез технологического процесса выполняют либо при выде­лении его из обобщенной структуры, либо в процессе проектиро­вания единичного технологического процесса. Машина вывода в обоих случаях позволяет иметь альтернативные варианты, позво­ляющие учитывать изменяющиеся условия в ПС.

При решении задач структурного синтеза с большим, но ко­нечным числом вариантов при условии, что их число и содержа­ние известны, используют алгоритмы направленного перебора (например, алгоритмы дискретного линейного программирования, алгоритмы последовательные, итерационные и др.). При возмож­ности синтез сводят к задачам полного перебора путем ограниче­ния области поиска на стадии формирования исходных данных.

Оптимальная стратегия обладает тем свойством, что при лю­бом пути достижения некоторого состояния (например, техноло­гического перехода) последующие решения должны принадлежать оптимальной стратегии для части маршрута обработки поверхнос­ти, начинающегося с этого состояния (технологического перехо­да). При решении подобных задач удобно использовать методы динамического программирования.

При решении задач структурного синтеза методом динамичес­кого программирования нахождение оптимального варианта дос­тигается в условиях определенности области допустимых перехо­дов на каждом шаге перехода. В более сложных случаях, когда зара­нее определить допустимость переходов невозможно, или в усло­виях неопределенности состава технологических операций следует использовать экспертные системы. Экспертные системы являются типичными системами искусственного интеллекта, в которых БЗ содержит сведения, полученные от людей-экспертов в технологи­ческой области знаний. Трудности формализации процедур струк­турного синтеза привели к популярности применения экспертных систем при структурном синтезе ТП, поскольку в них вместо вы­полнения синтеза на базе формальных математических методов осуществляется синтез на основе опыта и неформальных рекомен­даций, полученных от экспертов.

7.6. Разработка структуры и алгоритма процесса многообъектного технологического проектирования

Главной функцией интеллекту&чьного управления является ав­томатизация процессов анализа, принятия решении и на их осно­ве осуществление оперативного управления с непременным ис­пользованием текущей информации об управляемом объекте. Под управлением в данном случае будем понимать процесс, обеспечи­вающий точное и согласованное во времени взаимодействие от­дельных частей и элементов ВПС в соответствии с заранее разра-

294

ботанной программой управления на основе принятых решений. Методологической основой искусственного интеллекта является эвристическое программирование, при этом программа строится на базе принятых эвристик.

В процесс управления ВПС как составные части входят техно­логическое управление и организационное управление. Цель тех­нологического управления — получение требуемых свойств изде­лий; а цель организационного управления — формирование ВПС для реализации спроектированных ТП. Для этого необходимо обес­печение синхронизации взаимодействия ресурсов всех РПС, вхо­дящих в ОПС.

Особенностью управления в ВПС является:

• ограничение времени принятия решений;

• быстрое и частое изменение параметров ОПС.

В теории интеллектуальных систем синтез реализуется с помо­щью ЭС:

ЭС = <БД, БЗ, И>,

где БД — база данных, включающая сведения о базовых элемен­тах; БЗ — база знаний, содержащая правила конструирования ва­риантов структуры; И — интерпретатор, устанавливающий после­довательность применения правил из БЗ.

Системы искусственного интеллекта основаны на знаниях, от­деленных от процедурной части программ и представленных в од­ной из характерных форм. Такими формами могут быть продук­ции, фреймы, семантические сети. Реально функционирующие в современных САПР системы с БЗ чаще всего относятся к классу ЭС. Реализация систем искусственного интеллекта основывается на работе со знаниями: их представлении, хранении, использова­нии и т.д.

ВПС относится к разряду сложных систем, которые характери­зуются большим числом элементов и, что особенно важно, боль­шим числом взаимосвязей элементов. При создании ВПС имеет место смешанное проектирование — комбинация нисходящего (имеются в наличии отдельные готовые компоненты системы) и восходящего (имеются сформулированные требования ко всей си­стеме в целом) процессов. При таком проектировании возникает необходимость прогнозирования недостающих данных с последу­ющим их уточнением, т. е. последовательного приближения к окон­чательному решению (итерационное проектирование).

Структура ММ процесса многообъектного технологического проектирования представляет собой последовательность процедур поиска рациональной конфигурации ВПС. Первоначальной про­цедурой в структуре является определение необходимых ресурсов ОПС с учетом требуемой технической гибкости по условиям вы­полнения ПЗ, с одной стороны, и минимума задействованных

295

слоев, с другой. Поиск начинается с тех слоев, в состав которых входят специфическое технологическое оборудование, необходи­мое для выполнения соответствующих технологических операций (лазерная, электроэрозионная и т.д.) при изготовлении деталей, входящих в ПЗ.

Выбранные слои считаются базовыми. Следующей процедурой в структуре ММ является поиск (или выбор из базовых) тех слоев, которые способны обеспечить остальные более распространенные технологические операции. Таким образом формируется вариант компоновки ВПС.

Следующей процедурой в структуре ММ является определение наилучшего варианта последовательности запуска ПЗ в ВПС на выполнение. При этом для каждого варианта осуществляется про­верка на работоспособность, исходя из заданных требований. При получении варианта, не соответствующего требованиям, прово­дятся формирование и проверка следующего варианта, и так до нахождения предпочтительного.

При формировании очередного варианта сначала варьируют сроками запуска, а при отсутствии положительного решения ме­няют конфигурацию ВПС. На первом этапе выполняется попытка нахождения наиболее предпочтительного слоя и только при отсут­ствии положительного результата переходят к следующему этапу — изменению числа слоев. В этом случае выбор начинается со слоев, способных обеспечить наименьший прирост себестоимости изго­товления (минимальные транспортные расходы, минимальная се­бестоимость выполнения работ и т.д.).

При достижении приемлемого варианта на основе полученных данных формируется информация управления в ВПС. В связи с большим комплексом сложных процедур в структуре ММ техно­логического проектирования при формировании ВПС важное ме­сто занимают правильный выбор методов моделирования, а также их комбинация в зависимости от конкретных складывающихся производственных условий.

Для поиска предпочтительных решений при формировании ВПС следует использовать эволюционные методы, основанные на ста­тистическом подходе к исследованию ситуаций и итерационном приближении к искомому состоянию системы. Такой подход по­зволяет находить решения, близкие к оптимальным (рациональ­ным) за приемлемое время.

Одним из основных эволюционных методов является метод на основе генетических алгоритмов. Использование генетических ал­горитмов при формировании ВПС позволяет решать задачи с не-метризусмыми управляемыми параметрами (например, лингвис­тические).

Представление структуры формируемой ВПС в виде хромосомы позволяет генерировать ряд ее возможных вариантов, являющихся

296

аналогом популяции. Путем последовательных процедур, таких как кроссовер, мутации, верификация, селекция, оказывается возмож­ным путем последовательного образования новых поколений хромо­сом получать варианты структур ВПС, последовательно прибли­жающихся к оптимальному. При получении варианта структуры, удовлетворяющей заданной целевой функции, процесс считается завершенным, и полученный результат принимают за рабочий.

Формирование управляющих команд осуществляется на основе имитационного моделирования, использующего в качестве пара­метров модели параметры сформированной ВПС. На рис. 7.9 пред­ставлен алгоритм ММ процесса многообъектного технологическо­го проектирования с интеллектуальным управлением в ВПС.

Основные процедуры алгоритма сводятся к синтезу массива технологических операций, необходимых для выполнения ПЗ. На основе массива технологических операций происходит формиро­вание множества допустимых технологических маршрутов, неко­торые из них не являются оптимальными. Далее осуществляется

{ Начало )

Ввод исходных _/ данных

Синтез массивов вариантов ТП

Формирование варианта конфигурации ВПС

Формирование командной информации

Реализация

командной

информации

Q Конец)

Изменение параметров запуска ПЗ

Изменение

конфигурации

L

ВПС

Изменение состава

технологического

маршрута

Рис. 7.9. Алгоритм математической модели процесса многообъектного тех­нологического проектирования с интеллектуальным управлением в вир­туальной производственной системе

297

процедура формирования рабочей конфигурации ВПС, которая является итерационной. В ходе генерации вариантов структуры проводят имитационное моделирование, по результатам которо­го оценивают очередной вариант на основе целевых функций. При получении рабочего варианта выполняются процедуры форми­рования командной информации и управления ВПС. В против­ном случае осуществляется следующая итерация на основе при­нимаемого решения по изменению параметров моделируемой си­стемы.

Интеллектуализация процессов управления предусматривает формирование командной информации, базирующейся на приме­нении системы понятий прикладной области, использовании зна­ний в естественном виде, эксплуатации без программистов. Реали­зация концепции интеллектуализации опирается на развитые ме­тоды работы со знаниями: их представление, хранение, использо­вание и т.д. При этом под знаниями понимают систему понятий прикладной области, а также связь с их представлениями в фор­мальной модели; структуру данных информационной модели при­кладной области; математические модели, используемые при про­ектировании; правила принятия решений. Интеллектуальной сис­теме достаточно задать постановку задачи в виде требуемого ре­зультата и условий его получения. Последовательность операций, необходимых для получения результата, определяется системой автоматически.

Интеллектуальное управление в ВПС при многообъектном тех­нологическом проектировании опирается на принятие решений после определения значений выхода имитируемой системы при известных текущих значениях входных параметров, параметров системы и возмущений. Таким образом, можно записать

Я = F ( G , Z , U ),

где Н — вектор выходных параметров; F — оператор (программа) имитационной модели; G — вектор входных параметров; Z — век­тор параметров состояния системы; U — вектор параметров воз­мущающих факторов.

Имитационная модель является дискретной, поэтому в момен­ты времени /, переход системы из состояния (/- I) в состояние /" происходит скачком и представляет собой неделимое событие. На интервале времени [/,-, /,₊i] указанные выше параметры не меняют своих значений, полученных в момент времени t ,.

Входами модели дискретной ПС являются параметры ПЗ, вы­ходом системы — информация о конфигурации ВПС и сроки за­пуска ПЗ в нее на выполнение. В реальных ПС имеют место возму­щения, связанные с такими нештатными событиями, как сбои и отказы оборудования и оснастки. Виртуальная производственная система может находиться в одном из допустимых состояний, при

298

котором вектор параметров состояния системы не выходит за пре­делы ограничений (фонд свободного времени, состав технологи­ческого оборудования используемых частей РПС и т.д.).

Для успешного формирования ВПС в распределенных произ­водственных системах рекомендуется использовать CALS-техноло-гии, которые позволяют более эффективно создавать специфика­ции с информацией для программно управляемого технологичес­кого оборудования, достаточной для изготовления изделия. Этот процесс имеет протяженность во времени и пространстве и связан с многими организационно автономными проектными подразде­лениями.

Среди несомненных достижений CALS-технологии следует от­метить легкость распространения передовых проектных решений.

7.7. Разработка прогностической модели определения

сроков выполнения производственных заданий

в виртуальной производственной системе

При выполнении ПЗ в условиях экспериментального машино­строения большое значение имеет информация о сроках выполне­ния. Наличие этой информации позволяет правильно планировать загрузку вспомогательных служб производства (работу складского хозяйства, транспортных служб и т.д.), а также сроки изготовле­ния всего изделия в целом с целью синхронизации отдельных про­изводств (работы поставщиков и пр.). При отсутствии такой ин­формации организационно-производственные решения принима­ются в «состоянии неопределенности».

В условиях экспериментального машиностроения ПС представ­ляет собой сложную систему, которая в силу свойств и характера задач, возникающих при ее исследовании, требует учета большого числа составляющих ее взаимосвязанных и взаимодействующих между собой элементов. Данные элементы, являющиеся отдель­ными единицами технологического оборудования, обеспечивают выполнение некоторой достаточно сложной функции.

Для формирования информации о сроках выполнения ПЗ необ­ходима прогностическая модель, отражающая процесс функцио­нирования ПС во времени. Процесс прогнозирования выполнения ПЗ представляет собой совокупность упорядоченно связанных эле­ментов, которую необходимо рассматривать как систему с пози­ций анализа и синтеза. Такая модель характеризуется такими ос­новными параметрами, как: достоверность прогноза срока выпол­нения конкретного ПЗ и глубина прогноза сроков выполнения ПЗ.

Достоверность прогноза определяется степенью соответ­ствия полученной информации при использовании прогностичес­кой модели реальным срокам выполнения ПЗ. Достоверность про-

299

гноза снижается с увеличением отрезка времени, на котором осу­ществляется этот прогноз.

Глубина прогноза представляет собой отрезок времени, на лротяжепии которого точность прогноза выполнения ПЗ находит­ся в пределах заданной точности. С ужесточением требований к точности прогноза глубина его уменьшается. На достоверность и глубину прогноза существенно влияет уровень приоритета ПЗ, срок выполнения которого должен быть установлен.

Прогностическая модель может быть представлена в виде неко­торой информационной модели, основными частями которой яв­ляется информация о текущем состоянии ПС, информация о со­бытиях, происходящих в этой системе. Первая часть (информация о структуре ПС и ее параметрах) является детерминированной, вторая часть (информация о фактах поступления ПЗ, простоях оборудования по техническим причинам и т.д.) носит случайный характер и является стохастической. Поэтому при разработке про­гностической модели необходимо использовать количественные закономерности, связанные с получением, передачей, обработ­кой и хранением информации. С этих позиций при разработке про­гностической модели целесообразно использовать элементы тео­рии информации. На рис. 7.10 представлен алгоритм функциони­рования прогностической модели.

Состояние ПС, например Z, может иметь конечное множество значений х_ь х₂, .... х,„ с вероятностями соответственно Р_и Р₂, .... Р_т, т.е.

P ,= P ( Z ~ x ),

где P_t — вероятность того, что система ZnpHMeT состояние х,-; Z ~ х, — обозначение события (система находится в состоянии х,).

События в рассматриваемой модели могут быть в двух состоя­ниях: 1) событие свершилось; 2) событие не свершилось. Эти дан­ные представляют в табличной форме следующего вида:

 

*/	А	4
р /	р /	р {

Здесь индекс j обозначает принадлежность к определенному событию. Для каждого возможного события приведенная структу­ра одинакова. Различными оказываются только вероятности Р/.

Таким образом, имея статистический материал, можно пред­полагать с достаточной степенью достоверности на некотором интервале времени, как будет меняться состояние ПС и, следова­тельно, прогнозировать время завершения того или иного ПЗ.

Исходными данными являются характеристики событий, кото­рые могут иметь место в рассматриваемом интервале времени, и вероятность их появления. К таким событиям относятся поступле-

300

( Начало )

Ввод исходных данных

Определение величины приращения времени

Расчет степени влияния возмущающих факторов

Расчет величины энтропии системы

Фиксация

полученных

значений

Фиксация

полученных

значений

( Конец ^ Рис. 7.10. Алгоритм функционирования прогностической модели

ние очередного ПЗ в производство, остановка того или иного тех­нологического оборудования по техническим причинам и т.д.

При высоком уровне приоритета ПЗ прогностическая модель с достаточно высокой достоверностью позволяет определить срок его выполнения. Это вытекает из выражения, определяющего время Т, затрачиваемое на выполнение ПЗ:

где Т) — время выполнения /-й операции i-ro ПЗ; N — общее число технологических операций в маршруте обработки; ^,Т„_Ж — суммарное время, на которое производственный процесс изготов­ления прерьгоается вследствие занятости технологического обору­дования другими процессами.

Эта формула является математическим описанием прогности­ческой модели, позволяющим определять сроки выполнения ПЗ.

Чем выше приоритет ПЗ, тем меньше по величине составляю­щая Х^ож- При максимально высоком приоритете задания указан-

301

пая составляющая равна нулю и время его выполнения может быть определено по формуле

N

г = £7-;,

где N — число операций, необходимых для изготовления одного изделия.

Эта формула остается справедливой для всей части упорядо­ченного ряда ПЗ, для которой выполняется условие

М'у £ Л/_пс,

где My — информационный массив, определяющий весь набор операций, необходимых для выполнения ПЗ; Л/_пс — информацион­ный массив, определяющий технологические операции, которые могут быть выполнены в ПС; символ «•» указывает на то, что со­ставляющие массивов взяты за малый интервал времени At (A/—> 0). При невыполнении этого условия, но выполнении условия

jM ; dt < jM ' _nc dt

<\                        ' I

на интервале времени [_м, t ₂ ] большем, чем время выполнения са­мого трудоемкого ПЗ, оказывается возможным выполнение всего объема ПЗ. Однако выполнение части ПЗ будет иметь прерывистый характер во времени и, возможно, неоптимальный маршрут.

При невыполнении последнего условия данная ПС оказывается неспособной обслуживать поступающий объем заданий на отрезке времени ^ —1₂. В этом случае имеет место образование и рост оче­реди ПЗ на их выполнение. Если сумма времени пребывания ка­ких-либо ПЗ в очереди и времени их выполнения превышает сро­ки, установленные условиями, то можно считать, что данная ПС не в состоянии обслуживать данный поток заданий.

Компоненты £7^ являются случайными событиями с извест­ными вероятностями. Для определения глубины прогноза необходим критерий оценки точности математической модели определения априорной неопределенности системы Z, называемой энтропией.

Энтропия системы H ( Z ) определяется взятой с обратным зна­ком суммой произведений вероятностей на их логарифм:

/7(Z) = -X^log₂/i, 1=1

где т — число возможных событий на рассматриваемом интервале времени.

Логарифм в приведенной формуле взят с основанием 2, чтобы измерять энтропию в двоичных единицах. Изменение состояния ПС носит дискретный характер и требует рассмотрения всей сово-

302

купности состояний как сложной системы. В этом случае вероят­ность предполагаемого процесса изменения состояния системы оценивается следующим образом:

Р(х_ь х₂, ..., xj = P ( x_l ) P ( xd ... P ( xJ .

Откуда

log ₂ P ( x_f , x ₂ , ..., х_т) = \ og ₂ P { xi ) + ЬёгНхг) + ... + log ₂ P ( x_m ).

Тогда можно записать

Н(х„ х₂, .... х_т) = #(*,) + Н(х₂) + ... + Н{х_т),

т.е. при наличии нескольких возможных событий их энтропии скла­дываются. Таким образом, в общем виде

т

Н{х_и х_ъ ..., х_т) = £Я(х,)-/=1

Полученная формула позволяет получить объективную оценку степени неопределенности прогностической модели при варьиро-вании-ее глубины. При прогнозировании процесса изменения Z состояния ПС заведомо возникает некоторая степень неопределен­ности. Необходимо иметь в виду, что сведения, полученные о си­стеме, оказываются тем ценнее и содержательнее, чем больше была неопределенность системы до получения этих сведений.

Полученная формула позволяет оценить степень неопределен­ности прогнозируемого состояния системы в рассматриваемом интервале времени. При этом, чем выше вероятность предполагае­мых событий, тем больше глубина прогноза прогностической мо­дели. Таким образом, глубина прогноза определяется интервалом времени, на котором выполняется следующее условие:

% Щх,)<Н\

где т — число событий на данном интервале времени; Я* — вели­чина энтропии ПС Z .

Критическая величина энтропии Я' определяется совокуп­ностью факторов. Так, например, как указывалось ранее, для ПЗ высокого уровня приоритета величина энтропии стремится к нулю, так как вероятность поступления ПЗ с более высоким уровнем приоритета также стремится к нулю. Наоборот, на срок выполне­ния ПЗ с более низким уровнем приоритета будут оказывать влия­ние практически все вновь поступающие ПЗ, гак как уровень их приоритета будет выше.

При проведении работ по техническому обслуживанию техно­логического оборудования уменьшается «пропускная» способность производственной системы, так как из процесса производства вы-

303

тесняются задания с более низким уровнем приоритета заказами с более высоким его уровнем и период их изготовления возрастает.

Таким образом, чем ниже уровень приоритета ПЗ, тем боль­ше число случайных событий, влияющих на срок его выполне­ния, а следовательно, и величина энтропии для них выше. В то же время, критическая величина энтропии Ff для них выше вслед­ствие опять-таки низкого уровня их приоритета. Следовательно, для каждого ПЗ должна устанавливаться своя критическая вели­чина энтропии.

Критическая величина энтропии может быть определена из выражения

//*( Z )= - P '\ og ₂ P \

где Р* — допустимое значение вероятности того, что данное зада­ние будет выполнено в прогнозируемый срок.

Допустимая вероятность Р' зависит от многих факторов. На­пример, если уровень штрафа существенно ниже прибыли, кото­рая ожидается от принятия расчетного срока, то величина Р' мо­жет быть уменьшена (при этом энтропия системы возрастает и увеличивается глубина прогноза).

Наоборот, если ошибка в определении срока повлечет высокий штраф и срыв работ по созданию всего изделия в целом, то вели­чину Р' следует увеличивать (при этом уменьшается глубина про­гноза). Реально величина Р' определяется, исходя из заданных тре­бований к точности определения сроков выполнения ПЗ, произ­водственной ситуации и т.д.

Контрольные вопросы

1. Какие основные параметры определяют технологические возможно­сти существующих производственных систем?

2. Каким образом формируется обобщенная производственная система?

3. Какое значение имеет ВПС для выпуска новой продукции?

4. Опишите последовательность определения стратегии размещения производственных заданий и последовательности их запуска в производ­ственной системе.

5. Какое назначение и какую роль играют информационные обратные связи в ВПС?

6. Перечислите основные пути, позволяющие повысить точность ММ процесса функционирования ПС.

7. Какое значение имеет оценка ожидаемой себестоимости получаемых изделий на ранних этапах разработки ТП?

8. Какие два основных потока информации определяют процесс фор­мирования виртуальной производственной системы для выполнения ПЗ?

9. Какие факторы снижают точность получаемых результатов модели­рования процесса функционирования РПС и какими методами можно снизить их негативное влияние?

304

10. Что является основой для построения ВПС?

11. Какое влияние оказывает увеличение объема информации ОС на достоверность получаемых в результате моделирования результатов и уве­личение глубины прогноза?

12. Что такое интеллектуальное управление в ВПС?

13. Какие причины определяют необходимость использования интел­лектуального управления при формировании ВПС?

14. Какое назначение имеют прогностические модели при определе­нии сроков выполнения ПЗ?

15. Какие факторы влияют на глубину прогноза прогностической мо­дели?

I Зак. 519

Гл а в а 8

МАТЕМАТИЧЕСКИЕ МОДЕЛИ В РАСПРЕДЕЛЕННЫХ ПРОИЗВОДСТВЕННЫХ СИСТЕМАХ

8.1. Разработка информационной модели процесса функционирования отдельного производственного модуля

При поиске оптимальных условий функционирования произ­водственной среды необходима математическая модель, отражаю­щая изменения состояния технологического оборудования. При назначении загрузки той или иной единицы технологического обо­рудования исходят из заданной технологической операции обра­ботки и из текущего состояния производственной системы. Таким образом, поставленная задача является многопараметрической с широкой вариационностью.

На рис. 8.1 представлена взаимосвязь элементов структуры ПС. Из конструкторских подразделений производственные заказы по­ступают в технологические подразделения. Здесь осуществляется этап технологической подготовки производства. Кроме информа­ции о технологических аспектах производства на этом этапе долж­на формироваться информация организационного характера, оп­ределяющая последовательность и пути прохождения заготовок от момента их получения до завершения всех необходимых техноло­гических операций и получения готовых деталей.

Критерием эффективности при выполнении ПЗ является себес­тоимость и (или) производительность технологического процесса. С одной стороны, технологический процесс должен полностью обеспечивать выполнение всех требований рабочего чертежа и тех­нических условий на изготовление заданного изделия. С другой, в соответствии с экономическим принципом, изготовление изде­лия должно вестись с минимальными затратами труда и с мини­мальными издержками производства.

По результатам анализа возможных вариантов технологических процессов изготовления изделия выбирают вариант, обеспечива-

Конструкторское проектирование

Технологическая

подготовка

производства

Производственная среда

Готовые изделия

Производствен­ные заказы

Данные о текущей производственной ситуации

Рекомендации по изменению

конструкции отдельных

элементов изделия

Рис. 8.1. Взаимосвязь элементов структуры производственной системы

306

ющий наибольшую производительность и минимальную себесто­имость. Из вариантов с производительностью выше или равной заданной выбирают вариант с минимальной себестоимостью, на основе ИП, характеризующего технологию изготовления детали (Су) и время (f_;) запуска процесса изготовления соответствующего изделия:

ИП = <С,, С_ъ ..., С,, ..., С„; /,, t ₂ , .... U , ..., *„>,

где т — число наименований изделий в ПЗ, 1 < /' < т.

Каждый элемент С, является структурно-параметрической мо­делью процесса изготовления изделия /-го наименования. Время за­пуска /, каждого изделия определяется элементами С_{ и текущим состоянием ПС (рис. 8.2). Эта часть информационного обеспечения динамически меняется. Информация о текущем состоянии /-го про­изводственного модуля содержится в информационном потоке 2J.

Массив данных по всему парку технологического оборудова­ния, составляющего ПС, образует информационный поток Z, т.е.

" то

1=1 где п, ₀ — число единиц технологического оборудования в ПС.

Информационное обеспечение С, складывается из двух частей — постоянной, описывающей последовательность технологических операций, и переменной, описывающей тип технологического обо­рудования и момент запуска на нем очередной технологической операции. Первая часть информационного обеспечения формирует­ся на основе спроектированных ТП. Вторая часть информационного обеспечения определяется текущим состоянием производственной системы и является динамически меняющейся. Информацию о те­кущем состоянии производственной системы получают из инфор­мационного потока Z— массива данных по всему парку технологи­ческого оборудования, составляющего производственную систему.

Каждая единица технологического оборудования ПС ориенти­рована на выполнение операций по поддержке определенного ба­зового конструктива, однако целесообразно предусматривать ре­зервирование поддержки других, допустимых по технологическим признакам, базовых конструктивов. При назначении загрузки той или иной единицы технологического оборудования исходят из за­данной технологической операции обработки и из текущего со­стояния ПС. Таким образом поставленная задача имеет характер многопараметрический с широкой вариационностью. Концепту­альные решения при разработке математической модели должны быть такими, чтобы эта вариация не ухудшала ее достоверность.

При построении математической модели в качестве основных параметров, характеризующих состояние технологического обору­дования ПС, использовались следующие:

11*

307

 

гпм

Информация о техно­логических возможностях производственного модуля

пз,

Моделирование процесса

функционировани л производственного модуля

Информация о времени выполнения ПЗ

Информация о времени

доступа к произволстиен-

ному модулю

Рис. 8.2. Информационная модель функционирования гибких производ­ственных модулей:

/ — робот для загрузки заготовок и выгрузки изготовленных деталей; 2 — токар­ный станок с ЧПУ; 3 — подвижной стол с приспособлениями-спутниками для перемещения заготовок и деталей; 4 — фрезерный станок с ЧПУ; 5— робот для перемещения изготовленных деталей и загрузки заготовок; 6 — подвижной стол

308

• время освобождения технологического оборудования после завершения предыдущей технологической операции;

• время переналадки технологического оборудования с одной технологической операции на другую;

• длительность выполнения заданной операции;

• возможность использования полностью или частично элемен­тов наладки от предыдущей технологической операции для вы­полнения последующей.

Основными параметрами, характеризующими ПЗ, являются:

• множество технологических операций, выполнение которых необходимо для получения каждого ПЗ;

• возможные варианты последовательностей выполнения тех­нологических операций при выполнении каждого ПЗ;

• сроки выполнения ПЗ;

• требования к срокам выполнения ПЗ (штрафные санкции, взаимосвязь с другими ПЗ и т.д.).

Перечисленные параметры используются при выработке стра­тегии последовательности запуска ПЗ в виртуальную производствен­ную систему. Стратегия запуска предусматривает формирование последовательности моментов начала изготовления отдельных ПЗ. Эта последовательность является динамическим рядом, компоненты которого могут менять порядок следования и значения в зависи­мости от производственной ситуации.

При разработке стратегии запуска ПЗ возникает задача динами­ческого упорядочения сроков, для решения которой необходима разработка ММ, отражающей процесс взаимодействия компонен­тов ПС при выполнении ПЗ. Реализация такой ММ с помощью ЭВМ позволяет осуществлять оперативное управление последова­тельностью и временем запуска того или иного ПЗ в ВПС. Управ­ление ггтим процессом может осуществляться как r автоматичес­ком режиме, так и в режиме диалога «человек—машина».

В этих условиях обработка данных является многопарамстричес-кой задачей в условиях динамически меняющихся параметров ПС. Спецификой поставленной задачи является ее целочисленность и, следовательно, невозможность использования традиционных ме­тодов линейного программирования. Применение методов полно­го или направленного перебора в подавляющем большинстве слу­чаев оказывается невозможным в реализации вследствие большой размерности и неопределенности структуры процесса, даже с по­мощью высокопроизводительных ЭВМ.

Параметры ПС меняются согласно достаточно хорошо формали­зованным зависимостям и только в определенные, легко фиксиру­емые моменты. Отдельные, квантованные, отрезки времени имеют различную длительность, каждая из которых может быть определе­на на основе известных параметров производственных заданий и реализующих их ПС.

309

Необходимо систематизировать большое число параметров, ха­рактеризующих состояние ПС. Это выполнимо с использованием матричного представления коэффициентов, составляющих пара­метры ПС. Математическая модель представляется в виде двух мат­риц Zv \ В, описывающих состояние ПС в каждый момент.

Матрица Zтрехмерная, состоит из п слоев Д (рис. 8.3). Соответст­венно каждый слой, характеризующий технологические возможно­сти конкретной единицы технологического оборудования, представ­ляет собой двухмерную матрицу одинаковой размерности (т + 1) х т:

Д =

 

«1.1	«1.2   ■	••  «l.m
«2.1	«2,2   •	••  «2.m
ат,\	«m,2  ■	•• °m,m
°m+l,l	fl m+l,2 •	■• «m+l.»

(8.1)

где tn — общее число технологических операций, которые могут быть выполнены в данной производственной системе.

Время переналадки данного технологического оборудования с операции р на операцию q составит a_pq , где I < p , q < т. Отмстим, что а_РЧ = 0 при р - q . Время обработки одной заготовки на опера­ции q соответствует a_{mI q} .

Номер операции р

"\. г\

«1.4

" U

. ^fl U .

" г.*

а 2,4

°2,3

у Номер /операции д

" т,т

От.2

°/ n + I , i

° m +1.2

Число единиц

технологического

оборудования п

Рис. 8.3. Матрица свойств технологического оборудования производствен­ной системы

310

Если технологическое оборудование / идентично технологичес­кому оборудованию у, то выполняется условие

4 = 4

При описании свойств реального технологического оборудова­ния отдельные члены матрицы (8.1) могут оказаться неопределен­ными. Это происходит, если соответствующая операция не может быть выполнена на данном оборудовании.

8.2. Моделирование процесса функционирования совокупности модулей

Одним из наиболее важных этапов при определении рациональ­ной загрузки технологического оборудования является поиск оп­тимальной стратегии распределения ПЗ в ВПС. Поиск оптималь­ной стратегии является многошаговой задачей и предусматривает использование итерационных методов.

При разработке методики определения оптимальной загрузки технологического оборудования необходимо учитывать, что дан­ная задача имеет следующие особенности:

• большую размерность;

• зависимость последующей производственной ситуации не толь­ко от предыдущих условий, но и от трудно предсказуемых новых условий.

Для решения поставленной задачи целесообразен метод блоч­ного программирования, являющийся совокупностью приемов, позволяющих заменить решение крупных задач линейного програм­мирования решением ряда линейных экстремальных задач мень­шего объема. В этом случае можно сократить необходимую мощ­ность вычислительных процедур, более рационально использовать память ЭВМ, декомпозировать общую задачу на ряд задач, реша­емых методами, непригодными для решения общей задачи.

При блочном программировании часто используется метод раз­ложения, являющийся блочным аналогом метода последователь­ного улучшения плана.

Идеи блочного программирования не только упрощают вычис­лительные процедуры, но в ряде случаев расширяют область при­менения линейного программирования.

В дальнейшем, при определении загрузки технологического обо­рудования, необходимо для каждого конкретного ПЗ следовать этой стратегии.

Полная реализация такого подхода возможна при условии, что в любой момент пропускная способность ПС шире, чем требуется для одновременного обслуживания всего объема ПЗ. При этом дол­жно соблюдаться условие

311

M ' _Y с Мпс                                   (8.2)

где My — массив необходимых технологических возможностей ПС для выполнения ПЗ; Л/_пс — массив технологических возможнос­тей ПС; символ «♦» указывает на то, что составляющие массивов взяты за малый интервал времени (ДГ -» 0).

При выполнении условия (8.2) время выполнения всего ПЗ определяется временем выполнения максимального по трудоем­кости отдельного ПЗ. В этом случае время выполнения будет мини­мально возможным в соответствии с технологическими возмож­ностями технологического оборудования, на котором оно выпол­няется.

При невыполнении условия (8.2), но выполнении условия

JMydtlJMncdt ,                        (8.3)

когда t ₂ - Ц больше времени выполнения самого трудоемкого ПЗ, возможно выполнение всего ПЗ. Однако частично оно будет иметь дискретный характер и вестись, скорее всего, по неоптимальным маршрутам. Обращение условия (8.3) в равенство соответствует оптимальным технологическим возможностям ПС для выполне­ния заданного ПЗ.

При невыполнении условия (8.3) данная ПС неспособна об­служивать поступающий объем ПЗ на отрезке времени от t , до t ₂ . В этом случае отмечается и рост очереди ПЗ на их выполнение. Если суммарное время пребывания какого-либо ПЗ в очереди и его вы­полнения превышает сроки, установленные условиями, то данная ПС не в состоянии обслуживать данный поток заказов.

Будем рассматривать задачу поиска варианта оптимальной заг­рузки технологического оборудования, подразумевая выполнение условия (8.3) и невыполнение условия (8.2).

При перемещении заготовки от одного технологического обо­рудования к другому затрачивается время, которое определяется их относительным расположением на производственных площа­дях. Время перемещения заготовок между технологическим обору­дованием может быть представлено в виде матрицы В размернос­тью (п + 2) х п:

^ь \.\ ^ь\,г - К» *2, i b _{2 t 2} ... h . n

(8.4)

Ьп . п Ь„ +\, п Ьп +2 л

в= ......

b_n ,\ Ь_пЛ

^ л +2,1 " гн -2,2

312

где п — общее число единиц технологического оборудования, со­ставляющего производственную систему; b_pq — время перемещения заготовок от /?-го технологического оборудования к <7-му, причем 1 < р, q < п. Отметим, что Ь_рл = О при р = q .

Строка п + 1 содержит информацию о времени доступа к q -му технологическому оборудованию и определяет время завершения на нем предшествующей операции. Компоненты этой строки яв­ляются динамически меняющимися.

Последняя строка я + 2 содержит информацию о приоритете ПЗ, выполняемого на данном технологическом оборудовании. Кро­ме того, в данную строку при необходимости заносится информа­ция о потере работоспособности этого оборудования в текущий момент. Например, если данное технологическое оборудование не функционирует по причине проведения ремонтных работ, то в соответствующий элемент строки л + 2 записывается признак за­нятости но высшему приоритету, а в строке п + 1 — время досту­па, соответствующее предполагаемому времени ремонтных работ.

При поиске варианта оптимальной загрузки технологического оборудования следует исходить из сроков запуска каждого ПЗ и учитывать его оптимальный маршрут. При планировании загрузки технологического оборудования ПЗ с более ранним сроком посту­пает на технологическое оборудование согласно его маршруту об­работки. Затем выбирают следующее ПЗ с более поздним сроком запуска, и ему назначается технологическое оборудование соглас­но его оптимальному маршруту и т.д. Наконец, для очередного ПЗ складывается ситуация, когда в связи с загрузкой технологическо­го оборудования более приоритетными заказами невозможно обес­печить выполнение технологической операции по оптимальному маршруту. Тогда это ПЗ направляется на свободное технологичес­кое оборудование, для которого соблюдается условие

F { b_miJ + Ь_и + а_т+и + а_и) -> min ,

где Ь_П+и — члены матрицы (8.4); a_{m +] J} — члены матрицы (8.1).

Наилучший вариант выбирают в среде технологического обору­дования не только свободного, но и занятого ПЗ, с более низким уровнем приоритета. Если целесообразно использовать технологи­ческое оборудование, занятое заказом с более низким приорите­том, его место занимает заказ с более высоким приоритетом.

Очередной шаг At квантования по времени в математической модели определяется как минимальный из ряда доступа к тому или иному технологическому оборудованию:

At = min(£_n+,,, 6_я+|_ш2, ..., b„_+l„),                  (8.5)

где b „+\ j — члены матрицы (8.4).

После определения величины Д/ все .коэффициенты ряда (8.5) уменьшаются на эту величину, и далее процесс повторяется.

313

b „+\j = b_nJ - At при b_nJ > At,
b_n+\.i = 0     при b_nJi < At.

Таким образом, обеспечиваются условия, близкие к оптималь­ным, для обработки срочных заказов. Остальные заказы выполня­ются в режиме прохождения по мере освобождения технологичес­кого оборудования. Глубина этого режима для каждого конкретно­го ПЗ определяется его приоритетом.

При моделировании процесса загрузки технологического обо­рудования на каждом шаге фиксируют время поступления произ­водственных заказов на выполнение. Если на некотором этапе ока­зывается, что замещенный технологический процесс выполнения конкретного ПЗ по своей длительности не обеспечил выпуска хотя бы одной детали, возвращаются к этому моменту и данный техно­логический процесс снимают из рассмотрения на этом этапе.

Аналогично поступают и при появлении нового ПЗ. При воз­врате к ссютветствующсму моменту пересчитывают состояние ПС в той части, которая меняется, исходя из сроков запуска вновь поступившего ПЗ. В частности, если его сроки более ранние, пол­ностью пересчитывают загрузку технологического оборудования, если более поздние — пересчет не производят.

8.3. Моделирование процесса назначения очередности поступления заданий в производственную систему

Часто время поступления ПЗ на изготовление деталей, задан­ное в виде технологической документации, носит случайный ха­рактер. Для эффективной работы ПС необходимы упорядочение ПЗ и систематизация порядка их следования. Ввиду произвольного по­рядка их поступления такая система должна обладать достаточной гибкостью. Действительно, ранее может поступить ПЗ с длитель­ным сроком изготовления, а затем — срочное ПЗ с малым, «жес­тким» сроком изготовления.

Непосредственно формирование структуры ПЗ осуществляется на основе следующих их свойств:

• момент поступления;

• требования ко времени изготовления;

• трудоемкость изготовления;

• вид детали, определяющий технологию се изготовления.

С их учетом ранжируют ПЗ. Основным критерием ранжирова­ния является число технологических операций, выполнение кото­рых необходимо для получения готовой детали.

В качестве критериев, по которым была разработана структу­ра базы данных, выбраны: 1) уровень приоритета ПЗ; 2) число

314

оставшихся операций, необходимых для получения готовой де­тали.

Все ПЗ ранжируются в последовательности и в соответствии с этими критериями. Второй из них имеет целью сокращение време­ни нахождения ПЗ с малым числом оставшихся невыполненных технологических операций в производстве. Эта мера позволяет уменьшить объем незавершенного производства. На рис. 8.4 пред­ставлена модель распределения периодов изготовления деталей во времени.

Общий объем информации о производственных заданиях С, Одновременно находящихся в ПС, можно представить как сово­купность следующих информационных массивов:

С = (С\, С₂,..., С_п; С_{,С₂,..., С_/2; Q, С₂,..., C_{i 3} ),

где С/ — информационный массив данных об /-м ПЗ у-го уровня приоритета; j — уровень приоритета ПЗ;

Порядковый номер ПЗ на своем уровне приоритета /= [,..., i_t ; 1, ..., /₂; 1, ..., /з-

Отдельно взятый информационный массив представляет собой одномерную матрицу вида

С/=\У_и,Уг„...,К,...,У_м\,                       (8.6)

где V_u — вид технологической операции, / е [1, N ]; N1 — общее число операций, которые необходимо выполнить, чтобы полу­чить готовую деталь типа С/.

Этот массив динамически меняющийся, и в процессе выпол­нения технологических операций число его элементов уменьшает­ся. Кроме того, изменяется и массив С, так как отдельные ПЗ мо­гут менять свое положение в связи с тем, что внутри каждого уровня приоритетными становятся ПЗ с большим числом оставшихся тех­нологических операций, необходимых для полного изготовления готовой детали, т.е. при изменении этого показателя у какого-либо заказа, его положение в общем ряду / меняется и в каждый момент должно выполняться условие

/, < /₂ при Л7, < М₂.

Число компонентов и их состав в (8.6) меняется по мере вы­полнения отдельных технологических операций, поступления но­вых производственных заказов и выполнения ПЗ.

На рис. 8.4 показан вариант распределения времени на выпол­нение деталей отдельных ПЗ. При появлении нового ПЗ определя­ется его положение относительно поступивших ранее. Далее осу­ществляется упорядочивание ПЗ в сформированном ряду. Если в некотором количестве присутствуют ПЗ с аналогичными парамет­рами, то проводится сравнение числа операций последовательно с каждым, начиная с первого. Как только обнаруживается в рас-

315

tag

m

Ti

t ^ J

' нЗ ' hj ' ji ] ' я 2' »я

' ok 1 ' ok 2 ' ок/ 'окЗ ' ok л

Рис. 8.4. Модель распределения периодов изготовления деталей во времени:

т — общее число видов продукции; / — время изготовления деталей, мин; /_н3,

4и, 'и|, t„j, /,_lm — время начала изготовления деталей; /_№1, 1_тЪ /_OKj, 1_Ж„ — время

окончания изготовления деталей

сматривасмом ряду ПЗ с числом операций, большим, чем у вновь поступившего, вновь поступившему присваивается этот номер, а всем остальным, начиная со сравниваемого, присваивается но­мер, увеличенный на единицу.

Изменения вносятся в двух случаях: если поступил новый ПЗ или если закончилась очередная технологическая операция.

Таким образом, разработаны математическая модель и соответ­ствующие алгоритмы формирования структуры ПЗ, реализация которых с помощью ЭВМ позволяет автоматизировать процесс ранжирования ПЗ. При определении очередности поступления ПЗ на выполнение необходимо определить время запуска /_и„ каждого из них. Каждый из ПЗ имеет свой срок окончания выполнения /_дав и длительность его выполнения t „_{3 rat} . В целом, для всего ПЗ можно записать

'зап

— « 1 ЯН * И

(8-7)

'лап — 'зав 'изгог

где т — общее число видов продукции в ПЗ.

316

Оптимальным является случай, которому соответствует равен­ство в условии (8.7), однако он труднодостижим. В реальных про­изводственных ситуациях записанные условия имеют вид

' ззп — 'зав 'изгот 'нсзав 'поп

' ип — 'зав 'тгот 'незэв 'доп

где 'нсзав — время, в течение которого незавершенное изделие в виде полуфабриката находится вне производственного процесса (ожидание освобождения требуемого технологического оборудо­вания, вынужденный простой по организационным и другим при­чинам и т.д.).

Уменьшение времени на выполнение ПЗ может быть достигну­то за счет снижения /_нем„ и /_доп.

Величина *_незав определяется результатами технологического проектирования в ВПС.

Величина t_Bon эмпирическая величина, определяемая затратами времени, связанные с такими мероприятиями, как приобретение заготовок, выполнение операций на технологическом оборудова­нии и т.п.

Определение момента запуска /-го задания в ПЗ должно осуще­ствляться по результатам нахождения величины /£,„, где I < /"< tri .

Для сокращения величины /,_1сзав необходимо осуществлять уп­равление ресурсами ВПС таким образом, чтобы максимально сни­зить преждевременное выполнение ПЗ относительно его сроков.

8.4. Моделирование процесса функционирования

технологического оборудования виртуальной

производственной системы

Виртуальная производственная система может быть представ­лена в виде некоторой совокупности свойст в Z отдельных техно­логических единиц оборудования:

2"= (, А> Лг> -, Л. -■. ^Ап),

где А_к — некоторая совокупность технологических свойстк i - io тех­нологического оборудования, ппичем 1 < к < п, где п — общее число единиц технологического оборудования, образующих про­изводственную систему.

Технологические возможности производственной системы мож­но представить в виде информационного массива Л/_пс, представ­ляющего технологические операции, которые могут быть выпол­нены в данной производственной системе:

317

Л/nc =иЛ,

где А-, — массив технологических возможностей /-Й единицы тех­нологического оборудования производственной системы. При этом должны выполняться следующие условия:

1. Массив технологических возможностей производственной
системы должен содержать технологические требования базовых
конструктивов и обогащений; в противном случае ПЗ может быть
выполнено лишь частично;

2. Множество, образованное технологическими возможностями ПС, не должно существенно превышать множество, образованное технологическими требованиями базовых конструктивов и конст­руктивных обогащений; в противном случае возникает избыточ­ность, которая приводит к снижению эффективности функцио­нирования производственной системы;

3. Технологические возможности отдельных единиц технологи­ческого оборудования могут частично перекрываться (например, цилиндрическая поверхность может быть получена при использо­вании как токарного оборудования, так и фрезерного, расточно­го, обрабатывающих центров и т.д.).

Следовательно,

My с Л/_пс,

где Му- множество технологических операций, необходимых для обеспечения обобщенной структуры технологических процессов.

При несоблюдении этого условия часть технологических опера­ций, необходимых для выполнения конкретных производствен­ных заказов, окажется невозможной для реализации. Одновремен­но, мощность пересечения этих множеств должна быть максималь­ной.

Плотность распределения конкретных технологических опера­ций множества технологических возможностей должна соответство­вать плотности распределения требующихся технологических опе­раций, необходимых для обеспечения текущей совокупности про­изводственных заказов. Другими словами, ПС должна быть способ­ной обеспечить одновременное проведение однотипных операций без образования узких мест. В противном случае наблюдается сни­жение эффективности функционирования производственной сис­темы и уменьшение производительности.

При разработке математической модели ПС в качестве выход­ного параметра необходимо выбрать время обслуживания каждого ПЗ на отдельных операциях, так как именно этот параметр опре­деляет производительность ВПС. Этот параметр зависит от типа операции и технологического оборудования, на котором она вы­полняется. Конкретный тип технологического оборудования опре-

318

деляет время на транспортировку, на переналадку и выполнение операции. Время на переналадку определяется временем на разна-ладку с предыдущей операции и время на наладку для проведения следующей операции. В общем случае формула для расчета време­ни выполнения очередной технологической операции имеет сле­дующий вид:

Т/^+'^+'^+^Ч                                        (8.8)

где Tj — время на выполнение у'-й операции на к-м оборудова­нии; ( f — время на разкаладку /-го оборудования с предыдущей i_t операции; /}₍ — время на наладку /-го оборудования для выполне­ния операции y'j; t_A . — время на транспортировку производ­ственного заказа с А_к1 на А_к оборудование; /* — время обработки одной заготовки; и — число заготовок в производственном заказе. Для конкретного технологического оборудования формулу (8.8) можно преобразовать в следующую запись:

^T J = ^f h ^+/ A ^{+ t} Jⁿ -

Время на переналадку с одной операции на другую лежит в пределах

О < /_{( Wi} < /,, + t_A ,

где t_itJl — время переналадки технологического оборудования с /, операции Hav'i операцию.

Величина времени переналадки t_itJl определяется степенью пре­емственности технологической наладки от предыдущей операции к последующей в рамках одного и того же оборудования.

Время Т получения партии готовых деталей типа Q составит

N

где N — число операций, необходимых для изготовления одного изделия.

Используя (8.1) и (8.4), можно записать выражение для време­ни выполнения у'-й операции для некоторой С_гй заготовки на А;-м технологическом оборудовании:

V = * »*!.* + b_k„_k + a^jii,., + a$j,                       (8.9)

где Tf — время обработки партии заготовок типа С, на к-м техно­логическом оборудовании; b „^ _к — время, в течение которого ос­вобождается к-е технологическое оборудование; b_{kl k} — время пе­ремещения заготовок от места предшествующей обработки (обо­рудование А:,) и последующей (оборудование к); л„,_+К; — время обработки одной заготовки типа Q ; п_с. — число заготовок в партии типа Q; djj — время переналадки к-го технологического оборудо-

319

вания с предшествующей технологической операции /на следую­щую операцию/

Таким образом, на основе разработанной модели состояния производственной системы получена целевая функция. При вы­полнении условия

л

5)7)* —> min j - i повышаются коэффициент загрузки технологического оборудова­ния и производительность производственной системы в целом.

При невозможности выполнения всей совокупности техноло­гических операций в единой части РПС возникает необходимость перемещения полуфабриката в другую РПС. В этом случае возни­кают дополнительные затраты, в частности, времени, определить которые на перемещение полуфабриката из одной РПС в другую можно, используя пространственную модель.

Пространственная модель представляет матрицу D , структура которой описывает взаимосвязь между отдельными РПС, пред­ставленными матрицами (8.1) и (8.4). Параметры матрицы D — затраты времени на перемещение полуфабриката из одной РПС в другую. При необходимости такого перемещения формула (8.9) приобретает вид

V ⁼ *«+ut ⁺ **i.*^{+ а}л»|Л ⁺ ^ U + ^d r , _P , где d_{fJ >} — время, затрачиваемое на перемещение полуфабриката из г-й РПС в р-к>.

Исходя из требований максимального снижения затрат на вы­полнение ПЗ, необходимо при формировании конфигурации ВПС стремиться находить варианты, исключающие необходимость пе­ремещения полуфабрикатов между отдельными РПС.