При использовании детерминированных зависимостей в математических моделях, полученных по усредненным данным, из-за случайных отклонений возможен элемент неопределенности, влияющий на величину целевой функции. Поэтому очень важно проверить модель на чувствительность к такого рода случайным отклонениям. Большинство констант, показатели степени эмпирических зависимостей, характеризующие материал обрабатываемой заготовки, применяемый инструмент, метод обработки всегда имеют случайные отклонения от значений, принятых в математических моделях. Задача состоит в том, чтобы сравнить вектор рассчитанных параметров режима обработки и экстремум целевой функции, полученные по усредненным зависимостям, с их фактическими значениями, которые являются случайными. Лучшие режимы резания для конкретных условий обработки могут существенно отличаться от режимов, определенных по усредненным данным.
Возможную точность решения можно оценить величиной отклонений Ду и А^
& '=\?- Г\], (4.19)
А, =|х - X \,
где /*, х* — соответственно экстремум целевой функции и вектор оптимальных параметров режима резания, найденные по усредненным данным; /*, х' — действительные случайные величины. Ограничения, используемые в модели, могут иметь вид
g ,{ t , s , v )< blt
где bj — величины постоянных в правой части ограничений; / — глубина резания; s — подача; v — скорость резания.
156
Величины Ь, могут колебаться в пределах bimin - й1тах, что определяется видом ограничения, технологическими характеристиками используемого оборудования, материалом заготовки, требованиями к точности и качеству поверхностного слоя обрабатываемых деталей и т.д. Используя подход имитационного оборудования, находят отклонения от оптимальных параметров процесса и целевой функции, полученных по усредненным данным, значений этих же параметров и величины целевой функции, найденных при условии, что постоянные bt в ограничениях модели принимают свои крайние значения, каждое из которых имеет два уровня
Определив с помощью математической модели оптимальные параметры обработки и величину целевой функции для каждого случая предельных отклонений колебаний постоянных bh оценивают степень расхождения полученных характеристик с соответствующими значениями усредненного варианта. Определяют вероятность /'того, что А/И Ах (см. уравнение (4.19)) находятся в пределах заданной точности 5/и бх, т.е.
Р Р
| х--х1<8х}.
Для нахождения оптимальных режимов резания и экстремума целевой функции с заданными точностью и надежностью необходимо обеспечить выполнение следующих условий:
*-x1<5J>l-o,
где найденные режимы обработки и значение целевой функции будут находиться в заданных пределах с достоверностью (1 - а) (при оценке задаются вероятностью ошибки а = 0,05). Для сокращения числа вариантов возможно в первую очередь учитывать активные ограничения в усредненном варианте и рассматривать вариацию правой части ограничений Ь, только для их активной части.
4.G. Постановка задачи параметрического синтеза
Синтез подразделяют на параметрический и структурный. Проектирование начинают со структурного синтеза, при кото-
157
ром принимается принципиальное решение. Таким может быть, например, облик металлорежущего станка.
Примерами параметрического синтеза может служить определение геометрических размеров деталей, режимов резания и т. п. Задача параметрического синтеза может быть сформулирована как задача определения наилучших параметров при неизменной структуре проектируемого объекта. Такой параметрический синтез называют параметрической оптимизацией или просто оптимизацией.
В САПР процедуры параметрического синтеза выполняются технологом в интерактивном режиме либо на базе формальных методов оптимизации. Наиболее распространенной является детерминированная постановка, когда заданы условия работоспособности на выходные параметры У и нужно найти номинальное значение проектных параметров X .
Базовая задача оптимизации ставится как задача математического программирования
Extr/X*), X е Dx , DX ~[ X \ <p(Jf) > 0, у ( Х ) = 0},
где F ( X ) — целевая функция; X — вектор управляемых (проектных) параметров; <р(Х) и ц(Х) — функции ограничений; Dx — допустимая область в пространстве управляемых параметров X .
4.7. Постановка задачи структурного синтеза
Задачу структурного синтеза проектирования технологических процессов относят к наиболее трудноформализуемым. Поэтому структурный синтез, как правило, выполняют в интерактивном режиме при активной роли технолога-разработчика, а ЭВМ играет вспомогательную роль.
При структурном синтезе результирующее описание может содержать сведения о составе элементов структуры (наименование технологических операций), их числе и отношении порядка (последовательность технологических операций).
В процессе структурного синтеза выполняют задачу принятия решений (ЗПР), которую формулируют следующим образом:
ЗПР = < А, К, М, П >,
где А — множество альтернатив проектного решения; К = (кь /с2> ..., к„) — множество критериев (выходных параметров), по которым оценивается соответствие альтернативных решений поставленным целям; М: А -> К — модель, позволяющая для каждой альтернативы рассчитать вектор критериев; П — решающее правило для выбора наиболее подходящей альтернативы в многокритериальной ситуации.
158
|
|
Для упорядочения и описа
ния альтернатив используют ряд
подходов, в частности, морфо
логические таблицы и альтерна
тивные И-ИЛИ-графы в виде
деревьев (связных графов, не со
держащих циклов, т. е. замкнутых рис. 4.14. И-ИЛИ-дсрево, соответ-
цепей). ствующес морфологической таблице
Элемент морфологической таблицы М0 означает у'-реализацию /-й функции, описываемой матрицей М (в классе технических объектов).
Морфологическую таблицу представляют в виде отношения М
М = <Х, R >,
где X — множество свойств (характеристик или функций), присущих рассматриваемому объекту; R - < RU R 2 , ..., Rit ..., Rn > — множество значений (способов реализации) /-го свойства.
Далее морфологическую таблицу М можно представить в виде дерева (рис. 4.14). Часто применяются структуры деревьев, в которых используются логические функции И и ИЛИ (на рис. 4.14 темные точки — функции, а светлые — значения функций). Очевидно, морфологическая таблица содержит множество однотипных объектов, которые характеризуются одной или множеством функций. Ч-дерево удобно применять для описания структуры коп к ретного объекта. Оно представляет собой множество вершин и связывающих их ребер. Вершины разделены на ярусы. Каждый ярус состоит из параметрических уравнений, а вершины отображают части проектируемого объекта. Например, рассмотрим фрагмент И-дерева на рис. 4.15. Корневая вершина Мнулевого яруса отображает сложную систему проектируемого объекта (например, токарного станка мод. 16К20). Эта вершина соединяется ребрами с вершинами первого яруса, отображающими подсистемы (коробку скоростей, суппорт, фартук и т.д.) Вершины л-го яруса отображают базовые элементы (например, шпиндель, задний центр и т.д.).
При многообразии объектов используют многоярусные И-ИЛИ-
деревья. Двухъярусное дерево для разных типов объектов, в кото
ром предусматриваются разные подмножества функций, приведе
но на рис. 4.16. Например, такое
И-ИЛИ-дерево можно постро- д/
ить для разных станков токарной ^"t^ °"й яРус
группы. Его можно представить ^/^\^^
как совокупность морфологичес- %£• fks V jlk 1-й ярус
ких таблиц: каждая И-вершина.........................................
| • 4 W ^ i ••• -,:,, |
дерева соответствует частной
морфологической таблице, а
каждая ИЛИ-вершина инциден- Рис. 4.15. Фрагмент И-дсрсва
159
| Технические системы Типы систем |
| и |
| Л Функции |
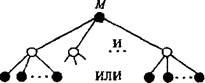
 ИЛИ щ •••■• Значения функций Рис. 4.16. Многоярусное И-ИЛИ-дерево
ИЛИ щ •••■• Значения функций Рис. 4.16. Многоярусное И-ИЛИ-дерево
тна 1-й ветви и соответствует множеству вариантов реализаций i - Pi функции. При этом /-я ветвь, исходящая из ИЛИ-вершины, отображает у-й вариант реализации.
Контрольные вопросы
1. В чем состоит математическое моделирование?
2. Какие требования предъявляются к ММ?
3. По каким признакам классифицируются ММ?
4. В чем суть структурных ММ?
5. Чем характеризуются табличные, сетевые и перестановочные ММ?
6. Для каких целей предназначаются функциональные ММ?
7. Назовите основные характеристики ММ на разных иерархических уровнях.
8. В чем заключаются особенности аналитических, алгоритмических и имитационных моделей?
9. В чем суть методики получения ММ?
10. Для чего необходимы преобразования ММ в процессе получения рабочих программ анализа?
11. Каковы особенности ММ на микроуровне?
12. Назовите особенности ММ на макроуровне?
13. Каковы особенности ММ на метауровне?
14. В чем заключается использование ММ на микроуровне?
15. В чем заключается использование ММ на макроуровне?
16. Какие ММ на метауровне можно описать путем использования целочисленного программирования?
17. В чем заключаются марковские случайные процессы?
18. Какие особенности возникают при использовании сетей Петри?
19. Какие задачи включает в себя постановка структурного синтеза?
Глава 5
Дата: 2018-12-28, просмотров: 514.