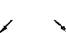| Значение параметра для ПР | модели | ||||
| ггр | ТРМ-50 | ТРМ-100 | ТРТ-2-250 | МИУ-7 | РТШ8- |
| ггь, кг | 50 | 100 | 250 | 250 | 50 |
| подвиж- | 2 | 2 | 3 | 3 | 2 |
| 13 ИЦИОКИ- | ±10 | ±10 | ±10 | ±3 | ±10 |
| ,1.-1 ■1й захвата | 2700 Неогран иченнь | 2800 >1 Й ±50 | 2000 30000 440 | 2200 Неог | |
| :щения м/с | 1,0 | 1,0 | 0,75 | 0,34 | 0,5 |
| :ния | Локальный автомат без памяти | На базе ЭВМ «Электроника-60» | Позиционная с автоматическим адресованием | Цикловая | Циклот |
Таблица 3.7
Технические характеристики транспортных напольных безрельсовых ПР
| Параметр | Значение параметра для IIP модели | ||
| КИЭ 2.2.0016 | «Электроника» НЦ-ТМ-03 | РБТ-1 | |
| Грузоподъемность, кг | 200 | 500 | 500 |
| Число степеней подвижности | 3 | 3 | 3 |
| 1 !огрешность позиционирования, мм: продольная поперечная | +5 ±5 | ±5 +20 | ±10 ±5 |
| Перемещение платформы, мм: вертикальное горизонтальное | 400 | 80 | 50 1030 |
| Угловые перемещений, ° | 90; 180; 270 | 90; 180,270 | — |
| Спсиа ние за трассой | По гироскопу | По с{юто-латчику | По фотодатчику |
| Скорость перемещения по трассе, м/с | До 1,4 | До 0,8 | До 1,0 |
• шаговые конвейеры с пульсирующим перемещением изделий
при cf орке, грузоподъемность этих конвейеров до 7 т при относи
тельно малых габаритах и простоте конструкции.
К напольно-тележечному внутрицеховому транспорту относятся:
• электропогрузчики и электротслежки (электрокары) грузоподъемностью до 0,5 т;
• электроштабелеры напольные грузоподъемностью до 2 т;
• транспортные напольные ПР (рельсовые и безрельсовые), смонтированные на тележках и управляемые по программе.
Монорельсовые транспортные ПР (напольные и подвесные) предназначены для межоперационного и внутрицехового перемещения деталей и изделий в условиях автоматизированного производства. Они перемещаются по принудительному маршруту, т. е. в строгом соответствии с заданной программой. ПР мостовые и напольные безрельсовые перемещаются по свободному маршруту, т.е. между любыми позициями загрузки (разгрузки), находящимися в пределах обслуживаемой зоны.
95
Напольные транспортные ПР движутся в соответствии с управляющими сигналами датчиков. Возможны следующие варианты движения напольных транспортных ПР: 1) вдоль провода, уложенного на глубине 40...60 мм от поверхности пола (по проводу пропускается ток силой в несколько сотен миллиампер с частотой 2...20 кГц и напряжением до 12 В; создается переменное электромагнитное поле, за которым следят датчики транспортного ПР и вырабатывают необходимый управляющий сигнал); 2) по светоотражающей полосе, прикрепленной к полу (слежение за трассой проводится с помощью фотосчитывающих датчиков, реагирующих на изменение световых потоков и вырабатывающих соответствующие управляющие сигналы); 3) по программе с использованием гироскопа. Технические характеристики транспортных напольных монорельсовых и безрельсовых ПР приведены в табл. 3.6 и 3.7.
В качестве накопителей могут использоваться автоматизированные склады, обслуживаемые штабелерами и транспортными ПР, и межоперационные магазины-накопители (напольные и подвесные). Магазины-накопители применяют в условиях поточного производства для деталей типа тел вращения. Подвесные накопители применяют в основном для корпусных деталей, для деталей сложной конфигурации.
Число единиц подъемно-транспортных средств для цеха (участка) определяют либо подробно с учетом грузопотоков, массы перемещаемых грузов, либо по данным базового производства.
Выбор транспортно - складских систем для автоматизированных производств
Система взаимосвязанных транспортных и складских устройств, используемая на АП для укладки, хранения, временного накопления, разгрузки и доставки предметов труда, технологической оснастки, называется автоматизированной транспортно-складской системой (АТСС).
При создании АТСС решаются задачи не только хранения заготовок, деталей, инструмента, оснастки, но и выбора наиболее эффективных, рациональных компоновок оборудования и маршрутов.
Существует два основных конструктивных варианта построения АТСС: с совмещенными и раздельными транспортной и складской подсистемами — автоматизированной транспортно-накопи-тельной системой (АТНС).
На рис. 3.11 показана схема ГПС с совмещенной АТНС. Станки / расположены параллельно стеллажу-накопителю 2. Кран-штабелер 4 перемещается вдоль фронта станков и обслуживает как стеллаж-накопитель, так и станки. По команде от системы управления кран-штабелер забирает из определенной ячейки стеллажа-
96
Рис. 3.11. Схема гибкой произвол- 2 3 4
ственной системы с совмещенной i \ i \i—i—r^
автоматизированной транспортно- ——т——
накопительной системой: /v-------- \ С
| пртш |
| □ |
I — станок; 2 — стеллаж-накопитель; 3— перегрузочный стол; 4 — кран-штабелер
накопителя необходимую заготовку и перемешает ее на перегрузочный стол 3 соответствующего станка. Готовые детали кран-штабелер забирает с перегрузочного стола и переносит в свободные ячейки стеллажа-накопителя. В данном случае не требуется специальной транспортной системы для обслуживания станков, так как эти функции выполняет кран-штабелер.
Схема раздельной АТНС с четырьмя стеллажами-накопителями / и двумя кранами-штабелерами 7 показана на рис. 3.12. В данной системе автоматическая транспортная тележка 5, перемещаясь по прямолинейному транспортному рельсовому пути 6, обслуживает несколько единиц технологического оборудования. Из стеллажного склада кран-штабелер 7 подает заготовки в таре на перегрузочный стол 2. Далее транспортная тележка по мере необходимости забирает с перегрузочного стола тару с заготовками и транспортирует ее к пристаночным накопителям 4. Установив тару с заготовками на накопитель, перегрузочное устройство транспортной тележки забирает тару с готовыми деталями и транспортирует ее на перегрузочный стол стеллажного склада. Затем кран-штабелер по команде от системы управления забирает тару с готовыми деталями и устанавливает ее в свободную ячейку стеллажа.
В приведенных компоновках использованы автоматизированные стеллажные склады-накопители, которые предназначены для приема, хранения, выдачи в производство и учета заготовок, основного и вспомогательного материалов, тары, инструментов, приспособлений, роботов, манипуляторов, готовых изделий, бракованных деталей, отходов производства с целью обеспечения эффективного производственного процесса переналаживаемой автоматизированной системы.
| ш ;ПТТ |
| 2 3 4 5 |
| аЩзЕь |
Рис. 3.12. Схема гибкой производственной системы с раздельной автоматизированной транспортно-накопительной системой:
| мм пидррщ-р I 1 1 I I 1 |
/ — стеллаж-накопитель; 2 — перегрузочный стол; 3 — станок; 4 — пристаночный накопитель; 5 — транспортная тележка; 6 — лранслортный рельсовый путь; 7 — краны-штабелеры
В зависимости от конструктивных особенностей и технической оснащенности выделяют следующие основные типы автоматизированных складов:
• клеточные стеллажные с автоматическим краном-штабелером или мостовым краном-штабелером;
• гравитационные стеллажные с краном-штабелером;
• элеваторные стеллажные;
• подвесные в сочетании с толкающим конвейером, имеющим автоматическое адресование грузов.
Наиболее распространены склады со стеллажными роботами-штабелерами, поскольку они весьма производительны, занимают мало места, легче автоматизируются. Робот-штабелер — напольная рельсовая машина, позволяющая накапливать заготовки и материалы в ячейках склада и осуществлять выдачу заготовок и материалов в стандартной таре или поддонах на приемно-выдающие устройства складов. Технические характеристики роботов-штабе-леров приведены в табл. 3.8.
В единичном и мелкосерийном производстве целесообразно применять стеллажные склады с автоматическими мостовыми кранами -штабелерам и.
При небольшой номенклатуре грузов и сравнительно больших запасах материалов, деталей используют автоматизированные склады с гравитационными стеллажами. Склады с автоматизированными элеваторными стеллажами целесообразно применять при малых грузопотоках, небольших сроках и запасах хранения грузов и малых размерах самих деталей и изделий.
Компоновка складов зависит от типа и характера производства, производственной программы, внутрицехового и внутрисистемного транспорта, характеристик производственного здания, где размещается проектируемый участок или цех, а также от типа и оборудования самих складов, их основных параметров.
Наиболее рациональна компоновка складов в ГПС, когда они максимально приближены к технологическому оборудованию. При этом кран-штабслер выполняет не только функции складирования, но и распределяет по рабочим местам материалы, заготовки, изделия, т.е. стыкует склад с технологическим комплексом. Один или несколько стеллажей склада помещается вдоль производственного участка рядом с оборудованием.
При линейных компоновках ГПС склады располагают в торцах производственного участка и оснащают стеллажными или мостовыми автоматическими кранами-штабелерами (рис. 3.13). При небольших грузопотоках роботы-штабелеры используют как транс-гюртно-складские роботы и для подачи заготовок на перегрузочные устройства. Мостовые краны-штабелеры используют при меньших, чем в случае стеллажных накопителей, грузопотоках и больших объемах хранения материалов, заготовок, готовых изделий.
98
Таблица 3.8
Технические характеристики складских роОотов-штабелероо
| Параметр | Значение параметра для модели робота-штабелера | ||||
| СА-05 | РШ-500 | С4225.02 | РСК-500 | РСК-1000 | |
| Грузоподъемность, кг | 500 | 500 | 500 | 500 | 1000 |
| Габариты тары, мм: длина ширина высота | 600 800 400 | 800 600 320 | 800 600 400 | 640 840 760 | 1260 860 750 |
| Высота помещения, м | 3,7...6,2 | 5,2 | 6,2 | 8,0 | 8,0 |
| Скорость перемещений, м/мин: горизонтального вертикального выдвижение захвата | 2...63 2...12 12,0 | 1...65 1... 18 10,0 | 2... 90 2... 80 10,0 | 0... 132 0...32 16,0 | 0... 160 0...32 16,0 |
| Погрешность позиционирования, мм: горизонтальная вертикальная выдвижение захвата | ±4 ±4 | ±2 ±4 ±3 | ±2 ±2 ±2 | ±5 +5 ±5 | ±15 ±15 ±10 |
| Габариты, мм: длина ширина высота | 3000 700 5400 | 3400 700 4760 | 2860 860 2800 | — | — |
| Управление | ЭВМ «Элек-трони-ка-60» | ЭВМ АСВТ М-6000 | |||
При большой потребной вместимости склада и небольшой номенклатуре хранимых материалов, заготовок, изделии целесообразна компоновочная схема с блочным гравитационным складом, которая позволяет эффективно использовать площадь и объем производственного здания (рис. 3.14). Подобные склады могут иметь компоновку с перпендикулярным в плане расположением стеллажей
4*
99
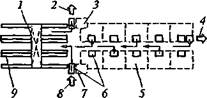
Рис. 3.13. Линейная компоновка склада в гибкой производственной системе:
1 — мостовой складской робот; 2 — выход готовых и бракованных изделий; 3 — участок ОТК; 4 — выход отходов производства; 5— производственный участок; 6 — перегрузочные устройства и накопители; 7 — участок входного контроля; 8— поступление материалов, заготовок, инструмента, тары; 9 — склад материалов, заготовок, инструмента, тары, готовых изделий
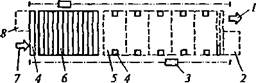
Рис. 3.14. Боковая компоновка склада в гибкой производственной сисгеме:
/ — выход готовых и бракованных изделий; 2 — участок ОТК; 3 — транспортно-складской робот; 4 — перегрузочные устройства и накопители; 5 — производственный участок; 6 — гравитационный склад заготовок, инструмента, готовых изделий; 7 — поступление материалов, заготовок, инструмента, тары; 8 — участок входного контроля
по отношению к рядам станков или линейную компоновку, при которой стеллажи ориентированы в том же направлении, что и ряды станков производственного участка. Последние ТНС предпочтительны в мелкосерийном производстве на предметно-замкнутых участках.
3.5. Сбооочные и подвижные роботы
Используемые в механосборочном производстве П Р выполняют работы, главным образом, по загрузке станков заготовками и снятию готовых деталей. Сборочные промышленные роботы (СР) применяются реже, а подвижные роботы (ПдР) предназначаются, как правило, для обследования цехов или производственных участков, в том числе с целью обнаружения возможных взрывоопасных объектов.
Сборочные роботы
Использование СР с контурной системой управления уменьшает трудоемкость сборки, однако для подготовки их УП требу-
100
ются увеличение затрат времени и высокая квалификация технолога-программиста.
Анализ около 100 позиций сборки и 300 рабочих мест в автомобилестроении показал, что 45 % операций составляют простейшие прямолинейные движения, 25 % — перемещения в двух направлениях и около 30 % — перемещения объектов сборки в трех направлениях. Для выполнения такого рода целенаправленных движений рука СР должна обеспечивать точность позиционирования и ориентации объектов в трехмерном пространстве, т.е. необходимо, чтобы манипулятор СР имел не менее шести степеней подвижности. По мере усложнения движений, выполняемых СР, процессы программирования становятся весьма трудоемкими.
Эффективным способом подготовки УП для СР по аналогии с подготовкой УП для станков с ЧПУ является система автоматического программирования. Задачи подготовки УП для СР решаются на основе технологических закономерностей, полученных для станков с ЧПУ, транспортных операций и неавтоматизированных операций сборки. Для подготовки УП требуются информация по логике анализа текущего положения СР и модель его движения (последовательность движений, элементы движений, координаты опорных точек, параметры движения).
В существующих в настоящее время системах автоматического программирования (САП) имеются отдельные элементы, позволяющие пользователю не решать задачи определения траектории движения и положения отдельных звеньев. Исходной информацией для автоматизации решения этих задач служат геометрические модели и описания внешней среды. Моделирование зарекомендовало себя как метод, обеспечивающий оценку реального поведения производственной системы при проектировании и возможность рассмотрения влияния на процесс проектирования разных комплексных параметров. Появление в производстве мощных процессоров, работающих в реальном масштабе времени с развитыми графическими средствами, создает основу для моделирования производственных задач, организации безлюдного производства, функционирующего без вмешательства человека-оператора. Наиболее совершенные системы подготовки УП СР представляют собой экспериментальные комплексы, однако они дороги и сложны. Их анализ позволяет сделать вывод об отсутствии систем, которые бы позволили полностью решить задачи проектирования УП СР в составе гибкого производства.
В процессе проектирования роботизированной операции можно выделить два качественно разных способа: проектирование для существующей технологии сборки и проектирование операции одновременно с конструированием изделия, представляющее собой триединый итерационный процесс, который заканчивается при достижении заданных технико-экономических целей проектирования (рис. 3.15).
101
Изделие
| Сборочная система | Технология сборки | |
| 1 | ||
| СР, иней шее технологическое оборудование |
Рис. 3.15. Схема технологической подготовки сборочной операции
В настоящее время большое распространение получил первый способ. Как правило, для проектирования РТК выбираются стабильные детерминированные операции. Проектирование включает в себя анализ технологичности собираемого изделия, выбор технических средств комплекса, компоновку РТК и подготовку УП. Анализ технологичности позволяет сформулировать требования к структуре комплекса, алгоритмам управления и программирования СР.
Любая схема сборки, отражающая последовательность выполнения технологической операции над объектом сборки (каждым его элементом), представляет направленный граф типа «сходящееся дерево» С( V , D ), где вершины ^отражают состояния технологической операции, а дуги D — движения, которые приноднт к данному состоянию. Чем меньше операций при прочих равных условиях требуется для сборки данного изделия, тем выше его технологичность. Число операций сборки пропорционально числу исходных компонентов изделия. Таким образом, наибольшую технологичность следует ожидать при числе сопрягаемых деталей, равном двум.
В общем случае в рассматриваемых операциях сборки можно выделить следующую последовательность движений: захват, транспортировка, поиск, контроль и др. В результате получается система, состоящая из некоторого подмножества микроэлементов движения. Возможности современных СР позволяют выполнять сложные технологические операции при ограниченных точностных характеристиках и небольшом числе простейших приспособлений благодаря применению микроЭВМ в контуре управления СР. Благодаря такого рода СУ возможны удобные и гибкие согласования технологических сборочных и контрольных операций в условиях складывающихся ситуаций, в результате повышается надежность сборочного процесса, обеспечивается успешное выполнение сборочной операции при наличии неточности позиционирования деталей, ошибок и помех. При использовании развитых СУ надежность выполнения сборочной операции может быть обеспечена с помощью простейших средств очувствления.
102
| Информация программирования |
| Язык высокого уровня |
| Оператор ( |
| Постпроцессор |
|
|
| Контроллер робота |
| X |
| Манипулятор |
Однако трудности внедрения СР связаны с необходимостью тщательного анализа технологичности конструкции собираемых деталей и сборочкой операции в целом и, как следствие, с упорядочением внешней среды, введением элементов адаптации, степень использования которых зависит от характера операции, применения систем искусственного интеллекта сложных эвристико-лрограммных генераторов цели, усложняющих получение УП.
| Рис. 3.16. Схема программирования роботизированной сборочной операции |
Современные системы подготовки УП, как правило, включают в себя методы обучения робота, автономного программирования и (или) их комбинацию. В общем случае автономное или текстовое программирование определяется как символьное описание операции и действий СР, которое может быть представлено последовательностью символов некоторого язьжа высокого уровня (рис. 3.16). При обучении СР оператор или технолог-программист проводит рабочий орган манипулятора по предполагаемой траектории перемещения и СУ в особом режиме, опрашивая состояние датчиков положения и записывая в память СР координаты звеньев. После этого записывается собственно программа взаимодействия СР с внешней технологической средой. Алгоритмы работы оператора, взаимодействующего с системой через клавиатуру и средства доступных ему пультов, зависят от целей, которые ставит перед собой оператор, особенностей системного пульта и особенностей состояния самого оператора.
Этот процесс может быть автоматизирован, если заранее знать значения переменных звеньев на некоторой координатной сетке. При этом программируются все фазы роботизированной сборки, а именно перевод захвата манипулятора к объекту сборки; захватывание объекта сборки; перемещение его к месту соединения; соединение. Когда изделие собрано, операция считается законченной.
Наиболее трудоемким этапом при разработке УП для роботизированной сборки является программирование локальных траекторий, так как оно выполняется программистом чаще всего неавтоматизированным методом. Предлагаемый подход основан на использовании принципов эвристического программирования, сочетающего алгоритм адаптации с системой формирования геометрических моделей собираемых деталей в системе САПР. Схема ал-
103
тп
Детали
Оборудование
 |  |  |
Анализ РМ *1 |
| Анализ ТП |
| а |
Анализ собираемых деталей
< п> -- - J <ф> 1 <ф>






 Технологическая схема сборки
Технологическая схема сборки
Характер элементов
движения фазы
соединения
т
Структурная схема
Анализ рабочей операции
Метод и алгоритм
формирования
движений фазы
соединения
_!_
J







 Последовательность
Последовательность
транспортных
движений
Характеристи ки
транспортного
движения
Характеристики логики управления




 Модель движения
Модель движения
Опорные точки
траекторий
транспортных
движений
Блок логики управления


 —(уп)~-
—(уп)~-
X
Модель логики операции
Рис. 3.17. Схема подготовки управляющей программы роботизированной
сборки:
ТП — технологический процесс; РМ — рабочая зона (СР и зона его функционирования); П — принятие решений; УП — управляющая программа СР
горитма такого подхода показана на рис. 3.17. Последовательность подготовки УП технологического процесса при использовании предложенного метода следующая:
объект сборки -> схема сборки —> сборочные движения —>
—» траектории перемещения объекта сборки —> -» геометрическая модель СР -» программа управления СР.
Общая идея метода состоит в использовании средств имитационного моделирования для подготовки опорных точек локальной траектории в САПР и последующей передаче их в СУ СР. Структура алгоритма включает в себя ряд этапов.
1. Подготовка геометрических моделей собираемых деталей в среде графического пакета САПР (при проектировании сборочного комплекса всегда можно выделить группу оборудования, обслуживаемого одним СР, и соответственно множество совершаемых им для этого движений с тем, чтобы для них проектировать УП).
104
2. Имитация разборки собранного изделия с записью промежуточных точек локальных траекторий в массив точек из условия отсутствия соударений разбираемых деталей в требуемой области или точке пространства (могут быть наложены и другие условия и ограничения со стороны внешней среды).
3. Выбор оптимальной последовательности опорных точек локальной траектории по какому-либо критерию.
4. Получение вектора для шарнирных переменных в каждой точке из кинематического уравнения СР при решении обратной кинематической задачи для каждой опорной точки траектории.
Если G ( X , Y , Z ) — точка, через которую проходит траектория, то координаты этой точки являются функциями шарнирных переменных
X - /i(6i> 62, 63, в4,..., 6„); Y = f 2 (0\, 62, 63, 64,..., 8„);
Z = /з(01> ^2, 63, 64, -.., 6„),
где 6,- — шарнирные переменные /-Й степени подвижности; / = 1, п — число степеней подвижности СР.
При решении этих алгебраических уравнений получают вектор шарнирных переменных для данной точки траектории.
5. Формирование управляющего воздействия на исполнитель
ные механизмы СР.
В результате укрупненного проектирования сборочной операции не вызывает трудностей программирование движений манипулятора и логики управления вне локальных траекторий перемещения одним из известных способов. Вместе с тем локальные движения фазы соединения осуществляются при значительных ограничениях технологической среды и требуют сложных траекторий, сочетающих перемещение по разным степеням подвижности. Такая траектория, если и удается ее запрограммировать, требует многократной отладки, так как выполняется без учета реальных скоростей и ускорений звеньев.
Определялась локальная траектория фазы соединения и выполнялась оптимизации последовательности опорных точек траектории. Обычно оптимизацию выполняют по времени т отработки
траектории: opt J dx (где tu t 2 — пределы изменения Бремени т).
Однако в рассматриваемом случае время не является лимитирующим фактором, так как при наличии точных данных по траектории на фазе соединения опорных точек более важным является отсутствие резких движений, которые могут вызвать смещение детали в захвате либо значительные отклонения от заданных программой координат опорных точек. Поэтому в качестве оптимизи-
105
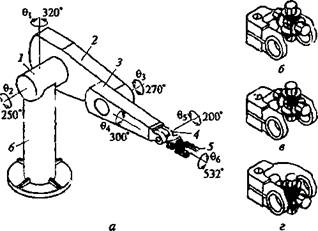
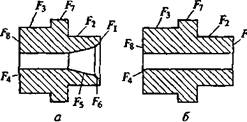
Рис. 3.18. Схема сборочного робота РМ-01 (о) и фрагменты моделирования как фазы (б—г) соединения вилки с крестовиной:
1 — плечо; 2 — рука; 3 — локоть; 4 — кисть; 5 — захват; 6 — колонна; 0,—66— шарнирные соединения i-й степени подвижности (/" = 1, ..., 6)
руемого параметра выбрана плавность движения v - const, a = = const (у — скорость движения оператора; а — ускорение движения органа манипулятора), тем более что микропроцессорные контурные системы управления роботом не обеспечивают постоянство и и а. На практике для стабилизации контурной скорости используют принцип равных интервалов. При обучении СР величина шага кошролируется с помощью наклеекной на линию контура ленты, на которую наносят метки через равные промежутки длины. Оператор с помощью пульта ручного управления записывает координаты в память СУ на каждом шаге.
На рис. 3.18 показан пример сборки карданного шарнира рулевого управления с применением робота РМ-01 («ПУМА 560») с шестью степенями подвижности, точностью позиционирования ±0,1 мм, антропоморфной кинематической структурой, максимальной скоростью перемещения 3000 мм/с, фузоподъемностью 2,5 кг и контурной СУ на базе встроенной ЭВМ. Выделены фрагменты моделирования соединения вилки с крестовиной кардана. Проведение имитационного моделирования фазы соединения сборочной операции позволило получить массив возможных опорных точек траектории.
Подвижные роботы
Из практики использования дистанционно управляемых ПдР для разовых специальных работ на объектах с организованной (упорядоченной) внутренней средой следует, что управление движе-
106
нием ПлР особенно в визуально не просматриваемых (по условию соблюдения требований безопасной работы) пространствах ставит перед оператором достаточно сложную задачу ориентирования и идентификации места нахождения ПдР по фрагментам телевизионного изображения внутренней (большей частью незнакомой) обстановки. Само же изображение на телевизионном экране в виде плоской масштабированной картинки не позволяет с достаточной объективностью оценить размеры предметов окружающей обстановки и расстояние до них (рис. 3.19).
Мобильные РТК легкого класса специального назначения, применяемые для проведения работ по обезвреживанию опасных предметов в условиях стесненных пространств, обычно имеют в своем
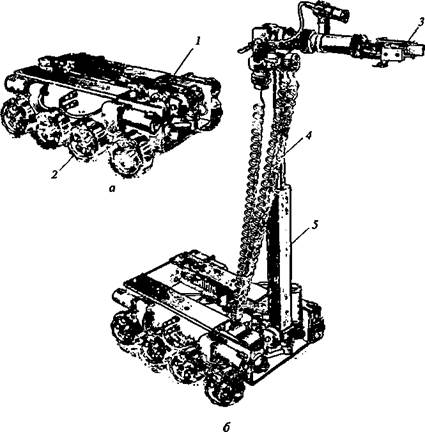
Рис. 3.19. Подвижной робот легкого класса в транспортном (а) и рабочем (б) состояниях:
/ — корпус робота; 2 — колеса движителя робота;.? — манипулятор; 4 — выдвинутая секция манипулятора; 5 — рука манипулятора
107
составе подвижной робот массой до 40 кг, который может переноситься одним человеком, и передвижной пост дистанционного управления, обслуживаемый одним оператором. Доставка такого комплекса может быть выполнена за минимальное время силами двух специалистов в доступное для человека место: помещения, салоны транспортных средств, территория промышленных объектов и т.д.
Особенностью ПдР легкого класса является расположение средств видеонаблюдения, как правило, ниже естественного уровня глаз оператора, что в значительной степени изменяет ракурс предметов окружающей обстановки и искажает восприятие действительности, а возможное отсутствие достаточной освещенности внутри объекта и необходимость применения в связи с этим локальной подсветки многократно усиливают эти искажения.
Потеря ориентации на объекте в силу перечисленных причин способствует неадекватной оценке ситуации и провоцирует оператора на ошибочные действия, что в конечном счете способствует срыву выполнения задачи. Поэтому представляется целесообразным изменить технологию управления движением ПдР таким образом, чтобы большая часть операций управления выполнялась техническими средствами, а у оператора оставались функции общего контроля и возможность корректировки процесса в неясных ситуациях.
Идея автоматизации процесса управления движением ПдР не нова и достаточно давно реализована для нескольких направлений применения ПлР, в частности, при движении роботизированного транспорта по регламентированным маршрутам в случаях перевозки заготовок, деталей и т. п. внутри объекта; для планетоходов в неопределенной среде; для транспортных средств (в основном военного назначения) по местности.
В подавляющем большинстве помещения, например производственные цеха, залы, комнаты, склады и т.п., выступают как пространства конкретных размеров и форм, имеющие опорные поверхности определенных свойств. Оборудование, расположенное внутри помещения, имеет известные (или достаточно просто определяемые) номенклатуру, конфигурацию, габаритные размеры и организованное (фиксированное) расположение как во внутреннем объеме помещения, так и по взаимному отношению. Каждому классу помещений присущи индивидуальные, наиболее характерные сочетания и параметрические значения факторов сопротивления среды. Исключение составляет объект поиска, для которого цель, конфигурация, размеры, расположение и свойства могут быть либо приблизительно известны, либо неизвестны совсем.
Модель помещения может формироваться либо непосредственно на месте проведения работ оператором, который с помощью сканера снимает с чертежа-планировки формализованное графическое описание помещения и вводит его в вычислительный комплекс внешней системы управления (ВСУ), либо при подготовке
108
к проведению работ до выезда на объект. Во втором случае модель формируется на внешних по отношению к ВСУ устройствах с последующей записью информации на магнитный носитель (дискету). Оператору остается ввести информацию в вычислительный комплекс ВСУ (с дискеты), проверить соответствие объекта и модели и при наличии отличий откорректировать модель.
Модели помещений транспортных средств ввиду неизменности их геометрического описания формируются на стадии заполнения базы данных ВСУ и затем пересылаются по указанию оператора непосредственно в вычислительный комплекс.
Полученная модель помещения подвергается обработке на предмет выделения свободных проходов для перемещения ПдР, образующих лабиринт, который может быть сформирован как автоматизированным, так и интерактивным способами. При автоматизированном формировании лабиринта помещение рассекается сеткой плоскостей, шаг между которыми и угловое положение в системе координат задает оператор. Из массива точек пересечения плоскостей с элементами контура помещения и границами запретных зон выделяются точки, образующие границы свободных проходов для передвижения ПдР, из которых, в свою очередь, и формируется лабиринт. В лабиринт включаются только те проходы, которые образуют кратчайший путь к месту назначения при условии соблюдения требований профильной проходимости ПдР (отсутствие непреодолимых препятствий).
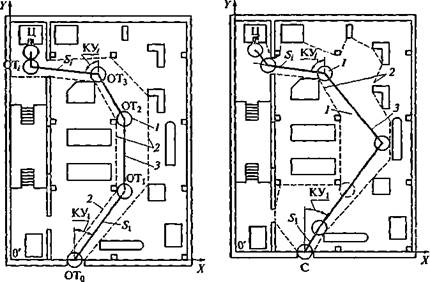
Знание координат места ПдР позволяет разработать стратегию поиска пути в лабиринте — траекторию движения. Способ формирования траектории движения ПдР определяется оператором в зависимости от сложности постапленной задачи и достаточности информации о внутреннем устройстве помещения и месте расположения цели. При задании траектории оператором на экран монитора ВСУ выводится фрагмент лабиринта, на границах которого оператор наносит опорные точки ОТ, —ОТ, предполагаемой траектории движения (рис. 3.20). Координаты опорных точек являются программными уставками на изменение параметров движения. По мере получения данных от средств измерения курсового угла КУ, пройденного расстояния и направления вращения движителей, а также от бортовых локаторов ПдР ВСУ корректирует фактическую траекторию при ее несовпадении с заданной, формирует и передает на борт ПдР соответствующие команды.
Уход ПдР с заданной траектории может происходить из-за его конструктивных особенностей (например, неодинаковой частоты вращения движителей разных бортов) либо под воздействием внешних факторов.
Другой способ формирования траектории — автоматизированный — осуществляет ВСУ. В этом случае оператор на фрагменте помещения, выведенном на экран монитора ВСУ, указывает только две
109
|
|
Рис. 3.20. Формирование траектории движения подвижного робота к точке-цели Ц по заданным опорным точкам ОТ в границах лабиринта, указанных оператором:
/ — область безопасности; 2 — границы лабиринта; 3 — траектория движения ПдР; КУ,—КУ,- — значения курсового угла; XO ' Y — система координат помещения; 5,, .... S , — длина участка траектории движения ПдР
Рис. 3.21. Автоматизированное формирование траектории движения подвижного робота из точки старта С к заданной точке-цели Ц по лабиринту, построенному управляющей ЭВМ:
/ — область безопасности; 2 — границы лабиринта; 3 — траектория движения ПдР; КУ!— КУ,- — значения курсового угла; XO ' Y — система координат помещения; St , ..., Si — длина участков траектории движения ПдР
точки — конечную точку пути (место расположения цели) и точку старта ПдР (рис. 3.21).
В данном случае траектория формируется следующим образом. Из /-й опорной точки проводится веер векторов курсовых углов в направлении цели и для каждого из них рассчитываются координаты точек пересечения с границами лабиринта. Из массива полученных точек пересечения выделяется точка, наиболее удаленная от ПдР. Угловое направление на эту точку берется в качестве курсового угла КУ, а расстояние до нее (за вычетом половины длины ПдР) — в качестве длины участка траектории движения S .
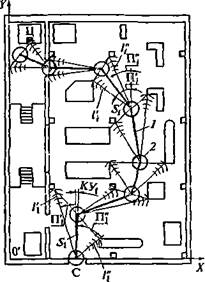
Формирование траектории в процессе движения ПдР сопровождается активной локацией лежащего впереди пространства (в секторе 180°). Значения пеленгов и расстояний до оборудования и препятствий передаются в ВСУ, которая рассчитывает текущие координаты места ПдР относительно предметов внутренней об-
110
|
|
Рис. 3.22. Автоматическое формирование электронно-вычислительной машиной траектории в процессе движения подвижного робота к заданной точке-цели Ц:
/ — траектория движения ПдР; 2 — область безопасности; С — стартовая точка робота; Х\\, П|", ■••> П/, U " — пеленги, определяемые локацией робота; /,', /,", .... //, //" — расстояния, определяемые локацией робота
становки и при необходимости корректирует координаты местонахождения ПдР, определяемые по показаниям бортовых средств контроля параметров движения (рис. 3.22).
Во всех случаях оператор контролирует поведение ПдР по фрагментам телеизображения, передаваемого бортовыми видеокамерами, а также по движению отметки на экране монитора ВСУ. В непредвиденных ситуациях оператор переходит на ручное управление.
Сценарий работы с использованием возможностей автоматизированной системы управления продиктован определенной последовательностью действий.
Оператор сканирует чертеж планировки или вводит готовое ее описание посредством считывающего устройства, после чего ЭВМ в автоматическом режиме создает модель среды.
Модель траектории перемещения ПдР в конкретной организованной среде формируется автоматически или вручную.
Управляющая ЭВМ создает модель движения робота в конкретной среде с расчетом уставок параметров движения на участках траектории с выработкой управляющих команд и выдает сообщение оператору о готовности к началу движения ПдР.
Оператор подает команду на начало движения ПдР и далее по мере перемещения его отметки к а экране дисплея и по наложенному на экран телевизионному изображению контролирует протекание процесса.
В непредвиденных случаях оператор имеет возможность взять управление на себя и после ручной корректировки движения ПдР вновь перейти на автоматизированный способ управления.
111
В процессе движения СУ отслеживает по показаниям датчиков чисел оборотов колес характер перемещений ПдР и в случае отклонения от расчетной траектории осуществляет корректировку фактической траектории перемещения робота. Корректировка осуществляется также в случае асимметричного преодоления препятствий (наезд на препятствие движителями одного из бортов), приводящего к отклонению ПдР от расчетной траектории из-за разности проекции на опорную поверхность путей, проходимых движителями разноименных бортов.
Подтверждением нахождения цели служит визуальное опознание цели оператором, а при отсутствии визуального контакта — наличие однозначно трактуемых сочетаний косвенных признаков. Цель опознается оператором в результате сравнения визуально видимых признаков найденного предмета на телеизображении с признаками на изображении из идентификатора базы данных на мониторе ВСУ или по совпадению полученного при обследовании найденного предмета сочетания косвенных признаков и признаков идентификаторов базы данных.
По окончании работы ПдР с целью он возвращается в точку старта по фактической траектории, рассчитанной и записанной ВСУ по данным бортовых средств контроля параметров движения. Петлевые участки, появление которых вызвано необходимостью коррекции ухода ПдР с расчетной траектории, спрямляются. Участки обхода препятствий спрямлению не подлежат.
За начальную точку траектории возвращения — репер — выбирается точка, в которой был осуществлен переход на ручное управление для непосредственного проведения работ с целью. Зга точка определяется ВСУ как начальная точка относительной системы координат рабочей зоны, в которой фиксируются все маневры ПдР.
Оператор контролирует процесс движения по видеоизображению бортовых телекамер ПдР и по поведению отметки ПдР в моделях лабиринта и помещения на экране монитора ВСУ.
Таким образом, ожидаемая практическая ценность применения ПдР складывается из следующих факторов: исключение субъективных ошибок оператора в оценке текущего местонахождения и ориентации ПдР в пространстве при его движении по спланированной трассе; сокращение времени выхода к заданной точке цели; сокращение потребления энергетических ресурсов на этапе движения к заданной точке и соответствующее увеличение доли энергетических ресурсов, расходуемых непосредственно на работу с целью, что необходимо при ограниченных объемах, выделяемых в конструкции ПдР легкого класса для размещения источников автономного питания; повышение надежности функционирования комплекса за счет создания параллельных ветвей управления, обеспечивающих независимый переход с одной ветви на другую.
112
3.6. Компоновочные схемы автоматизированных производственных систем
Компоновка АПС определяется технологическим процессом, его конструктивно-технологическими особенностями, а также заданным объемом выпуска изделий, конкретными условиями производства и характеризуется структурой технических средств и схемой их расположения.
Структура технических средств — качественный и количественный состав основного и вспомогательного оборудования — зависит от характера производственного процесса и объема выпуска изделий. Например, форма специализации производственной системы определяет однотипность и взаимозаменяемость технологического оборудования, наличие межоперационных заделов вызывает необходимость включения в АПС магазинов-накопителей, межоперационная передача деталей в процессе обработки требует единой транспортной системы, а работа по принципу «склад — станок — склад» — локальных транспортных систем. Необходимость межоперационного контроля требует организации контрольных постов, тогда как в случае автоматизированных средств контроля в процессе обработки деталей в составе оборудования контрольные ячейки внутри АПС не требуются.
От принятой системы управления и степени ее автоматизации зависит включение в компоновку управляющих устройств (диспетчерских пультов, систем ЧПУ, средств сбора и передачи информации, ЭВМ различного уровня).
Основными факторами, влияющими на состав элементов компоновки, т. е. на структуру технических средств, являются:
1) форма специализации участка, цеха;
2) тип оборудования;
3) особенности АТНС и АТСС (наличие межоперационных заделов, работа по принципу «склад — рабочее место», автоматизация межоперационной передачи изделий);
4) особенности системы инструментального обеспечения («жесткое» оснащение станка, комплектование магазина на складе);
5) особенности системы контроля (виды контроля, применяемые средства);
6) особенности системы уборки стружки (механизированно-ручная, автоматизированная);
7) тип и принципы СУ (локальное управление компонентами системы, групповое управление оборудованием, комплексно автоматизированное управление).
Схемы расположения элементов АПС зависят также от характера производственного процесса и конкретных производственных условий (наличия производственных площадей, размещения АПС в цехе, расположения коммуникаций).
113
Специализация переналаживаемых производственных систем на базе оборудования с ЧПУ
Под формой специализации производственного подразделения понимают процесс разделения труда, в основе которого лежит обособление изготовления изделий или выполнения отдельных видов работ. Различают три основные формы внутризаводской специализации: предметную, технологическую и смешанную (предметно-технологическую).
При предметной форме специализации изделие (деталь, узел, агрегат) изготавливается полностью в одном подразделении (участке, цехе). В зависимости от объекта специализации различают предметно-подетальную и предметно-узловую формы специализации.
Технологическая специализация характеризуется сосредоточением в одном производственном подразделении изготовления разных изделий, объединенных по общности выполнения одинаковых видов работ или операций.
Смешанная (предметно-технологическая) форма специализации характеризуется сочетанием признаков предметной и технологической форм специализации подразделений.
За основной принцип формирования участков на базе оборудования (станков) с ЧПУ принята конструктивно-технологическая однородность изделий (деталей), которая является наиболее правильным принципом их совмещения.
При определении вида и формы специализации подразделений для обработки заданной совокупности деталей используют следующие показатели:
1) число операций, выполнение которых возможно и целесообразно на оборудовании с ЧПУ, и удельный вес таких операций — Ко„ ЧПУ;
2) суммарное число операций, выполняемых на оборудовании (станках) с ЧПУ по технологическим процессам (/ ~ 1, ..., п) изготовления всей совокупности деталей — А*оп,-;
3) удельный вес трудоемкости операций, выполняемых на станках с ЧПУ, в общей трудоемкости изготовления всей совокупности деталей — А^цпу;
4) удельный вес трудоемкости операций, выполняемых на станках с ЧПУ, по видам работ в общей трудоемкости данного вида работ по изготовлению всей совокупности изделий — Кгр ЧПУу.
При минимальных значениях Коп„ невысоком Kon ,{ l } V и небольшой трудоемкости операций использование оборудования с ЧПУ нецелесообразно.
Возможна организация подразделения для выполнения данного вида работ на станках с ЧПУ для совокупности деталей других подразделений (участков цеха) с технологической формой специализации.
114
При малом значении Я"опчпу> но большой трудоемкости данного вида работ по изготовлению совокупности деталей на станках с ЧПУ организуется подразделение (участок, цех) на базе станков с ЧПУ данного вида работ с технологической формой специализации для обработки рассматриваемой совокупности деталей.
При высоком значении Koni , но малой трудоемкости изготовления деталей на оборудовании с ЧПУ его встраивают в производственный процесс с учетом норм обслуживания, т.е. организуют зону обработки совокупности деталей на оборудовании с ЧПУ внутри данного подразделения.
При высоких значениях Коп, и К^ чпу проводится расчет АоП чпу-
При высоком значении Л„пчпу для конкретного (/) вида работ с учетом норм обслуживания возможна организация производственного подразделения на базе станков с ЧПУ у'-го вида работ для обработки рассматриваемой совокупности деталей с технологической специализацией.
По остальным видам работ при А^чпу—» min организуют предметно-замкнутое подразделение (зона, участок, цех) с учетом норм обслуживания станков с ЧПУ и степени замкнутости подразделения.
Особенности оборудования с ЧПУ, в том числе обрабатывающих центров, приводят к необходимости выделения их в определенные зоны обработки, отличающиеся высоким уровнем автоматизации обработки и управления. Число зон станков с ЧПУ, их расположение зависят от конструктивно-технологических особенностей обрабатываемых деталей.
Выбор форм организации производства в автоматизированных системах
Целью организации производственного процесса является достижение максимально возможных для данных условий производительности, ритмичности и непрерывности процесса, специализации технологических позиций. Различная степень достижения этих принципов для конкретного производственного процесса определяется формой его организации.
Переналаживаемые производственные системы могут иметь все формы организации производства от АЛ до АУ с разной степенью автоматизации. Однако каждая форма организации применительно к АП имеет свою специфику.
Для АЛ на базе основного и вспомогательного оборудования с ЧПУ характерна возможность изготовления группы изделий за счет габ-кости (переналаживаемости) технологического оборудования. Хотя операторы выполняют в основном функции наладки, подналад-ки, переналадки при смене объектов производства, управления и наблюдения, допускается выполнение ими начальных и конечных загрузочно-разгрузочных и контрольных операций.
115
Для поточных линий характерно следующее: прямоточность движения изделий в процессе их изготовления; расположение оборудования в последовательности выполнения технологических операций; полная или частичная (для прерывисто-поточных линий) синхронизация операций; возможность переналадки оборудования.
На автоматизированных поточных линиях большинство операций производственного процесса выполняются с помощью средств автоматизации. При этом использование ручного и механизированного труда допускается только на отдельных операциях.
На частично автоматизированных участках используется оборудование как с ЧПУ, так и с ручным управлением. Для таких участков характерно следующее: автоматизация большинства технологических операций; наличие переналаживаемой АТНС для производственных ячеек, АСС и АСИО; групповое управление оборудованием с ЧПУ. При этом, так же, как и на поточных линиях, допускается использование ручного и механизированного труда на отдельных операциях.
Характерными чертами комплексно автоматизированных участ ков является следующее: выполнение всех операций всех технологических процессов с помощью средств автоматизации; применение ПР; наличие АТНС, АСС, АСИО и АСУ всего участка. Операторы выполняют только функции наблюдения, регулирования и переналадки оборудования при смене объекта производства.
Особенности АПС в вопросах организации производственных процессов следующие:
1) тесная увязка основных и вспомогательных (обслуживающих) производственных процессов (приводит к необходимости создания комплексного технологического процесса);
2) изменение роли АТСС в общем производственном процессе: склад становится центром планирования, учета и регулирования производственного процесса в АПС, а транспортная система — ее стержнем;
3) отсутствие жестких требований к размещению основного оборудования (например, строгого расположения оборудования по ходу технологического процесса);
4) повышение требований к техническому обслуживанию АПС: жесткая регламентация качества и времени выполнения ремонтных и наладочных работ;
5) повышение требований к обеспечению надежности АПС за счет применения средств и методов диагностики состояния оборудования и инструментов;
6) применение системы резервирования для обеспечения надежности функционирования АПС (например, увеличение числа единиц оборудования, использование накопителей);
7) комплексность и высокий уровень автоматизации процессов управления;
116
8) интеграция ЛСУ ТП и САПР, применение информационных технологий на всех стадиях подготовки производства.
Основные принципы и примеры компоновок
автоматизированных систем разного
организационного уровня
Компоновка автоматизированных систем определяется технологическим процессом, конструктивно-технологическими особенностями и заданным объемом выпуска изделий, конкретными условиями производства и в зависимости от этого характеризуется структурой технических средств и схемой их расположения.
При определении структуры технических средств должен реа-лизовываться системный подход к анализу и синтезу АПС как сложных технических систем. Системный анализ включает в себя:
• классификацию АПС по признаку сложности;
• формулирование (выделение) системных свойств АПС;
• введение понятий структур АПС как способов организации внутрисистемных связей;
• формирование критериев эффективности функционирования АПС.
Результаты анализа совместно с соответствующими БД используются для последующего структурного синтеза автоматизированных систем. В БД хранится информация о классификации объектов производства, групповых технологических процессах, конструктивно-технологических параметрах оборудования, компоновочных решениях АПС и т.д. Эффективность работы с БД при принятии решений напрямую зависит от степени использования информационных технологий как при системном анализе, так и при системном синтезе структур АПС.
Синтез конкретной структуры предполагает ее выделение из множества возможных вариантов с использованием критериев эффективности функционирования АПС, сформированных на стадии системного анализа.
Для оценки результатов синтеза структуры проводится математическое моделирование работы спроектированной АПС с последующим анализом результатов моделирования.
Ввиду сложности решаемых задач и большого объема перерабатываемой информации при анализе и синтезе структур АПС целесообразно использовать методы поискового конструирования, обеспечивающие выбор структуры автоматизированной системы по заданным критериям (прямая задача) и определение области ее рационального применения по известным параметрам (обратная задача).
В зависимости от принятого разделения производственного процесса различают АПС с предметной и с технологической формами
117

 2
2
/ "*" 3 —+- 4
-^—
Рис. 3.23. Вариант компоновки для предметно-замкнутых автоматизированных участков:
/ — зона подготовки баз; 2 — зона станков с ЧПУ; 3 — автоматизированный склад; 4 — цехи-потребители; 5 — зона станков с ручным управлением
специализации. В предметно-замкнутых АПС полностью или частично изготавливают одно изделие или группу изделий, а в АПС с технологической специализацией выполняют отдельные виды работ для широкой номенклатуры изделий.
На предметно-замкнутых АУ выделяют зоны оборудования с ЧПУ и зоны оборудования с ручным управлением. Различают также зоны предварительной, основной и окончательной обработки. В зонах предварительной и окончательной обработки применяют в основном оборудование с ручным управлением.
На рис. 3.23 представлен вариант компоновки предметно-замкнутого АУ, где зоны обработки деталей на станках с ЧПУ и ручным управлением разделены автоматизированным складом 3. Внутри зон может быть предусмотрена межоперационная передача деталей. Аналогичную компоновку могут иметь участки с технологической формой специализации, где в зонах 2 и 5 выполняются определенные виды работ на однотипном оборудовании для разных изделий.
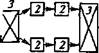
На предметно-замкнутых АУ в связи с разными затратами времени Тпп по операциям появляется необходимость создания межоперационных заделов и, следовательно, размещения магазинов-накопителей внутри производственной системы. Примеры вариантов расположения магазинов-накопителей на участке приведены на рис. 3.24.
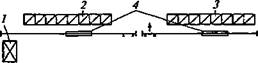
Транспортная система в ПС может быть локальной и единой для всего подразделения. По расположению различают линейные и круговые транспортные системы (рис. 3.25). Расположение оборудования внутри зон обработки такое же, как и в обычных подразделениях: последовательное, параллельное, смешанное.
В случае применения приспособлений-спутникоп в компоновке участка необходимо предусмотреть погрузочно-разгрузочные позиции или станции для установки и съема деталей с приспособлений. Расположение этих позиций (рис. 3.26) или станций на участке зависит от принятой системы обеспечения обрабатывающего оборудования деталями в приспособлениях-спутниках и соотношения времени обработки деталей на станке и времени их установки-снятия.
118
|
|
fll 111

u^^
/
^2 И2И1^УА2И2И2}^
|
|
| чть |
1
Рис. 3.24. Варианты расположения магазинов-накопителей на автоматизированных участках:
а,б— магазин-накопитель соответственно у каждого станка и у группы станков;
в, г — единый магазин-накопитель соответственно в начале и в середине участка;
д — промежуточные магазины-накопители; / — автоматизированный склад; 2 —
обрабатывающее оборудование; 3 — магазин-накопитель
| -- 0 0 2 ттг тэт т |
| 1 ■*- 3 — \ |
| гД гМ гЩ 2 0 2 |
| /^ | -С*- |
| Щ Д! Щ t ♦ 141 W ТЭТ * | |
| -- 0 0 0 щ тэт m / |
| -^1 * |
Рис. 3.25. Варианты расположения транспортных систем:
а — линейная; б — круговая внешняя; в — то же, внутренняя; / — автоматизированный склад; 2 — модуль, обрабатывающий центр, станок с ЧПУ; 3 — единая линейная транспортная система; 4, 5 — единая круговая замкнутая транспортная система соответственно внешняя и внутренняя
119
CZI
-A «Ь -j
-*-<r
U.
| 1, | 4 | ~S |
|
I 1 | ||
d
^Ats eMii й
cap ci mm s
II II
 FT
FT
| * 1 |
| ||
| * it! | |||
| 4 -* » | |||
|
| i- |
| |
| 1 S\ 1 1 | |||
|
| |||
| И | 5| I I | ||
| Ti | ' | ||
| -a- | |||
| 1 | / | |
| L | 2 J | |
| ♦ t 4 | ||
| ~^_ | ||
| 1 | II |5| i | |
Рис. 3.26. Варианты расположения погрузочно-разгрузочных позиций:
а — обеспечение погрузочно-разгрузочных позиций всех станков ПС через общий накопитель: б — доставка деталей, установленных в приспособления-спутники на погрузочно-разгрузочных позициях, к станкам через накопители для групп станков; в — то же, непосредственно к станкам; г — расположение погрузочно-разгрузочных позиций в отделении склада; / — автоматизированный склад; 2 — погрузочно-разгрузочное устройство (станция); 3 — накопитель; 4 — транспортная система; 5 — обрабатывающее оборудование
Если установка деталей выполняется на складе, то погрузочно-разгрузочные позиции располагают в отделении склада. При большом значении времени непосредственной обработки детали на станке Гмаш и относительно малом Твс„ (вспомогательное время установки-снятия детали) обеспечивают погрузочно-разгрузочные позиции всех станков участка через общий накопитель или непосредственно подают детали к рабочим местам. В последнем случае к каждому рабочему месту детали в приспособлениях доставляют либо с помощью транспортной системы непосредственно на станки, либо в накопители к каждому рабочему месту, либо в накопители для групп станков. При определенном соотношении Гмаш и Г^,, возможна установка погрузочно-разгрузочных позиций на группу станков внутри подразделения.
В зависимости от принятой формы организации производства, разработанного технологического процесса обработки и сборки изделий, уровня его производительности, гибкости и автоматизации выделяют три основные группы компоновочных схем АПС.
120
К первой группе относятся ЛПС, организованные по принципу участков для мелко- и среднесерийного производства с автоматизацией транспортно-складских операций. В состав таких АПС включаются станки с ЧПУ для изготовления закрепленной за системой номенклатуры изделий, а также универсальное или специализированное оборудование, не оснащенное ЧПУ.
На рис. 3.27 показана переналаживаемая система для обработки корпусных деталей в условиях многономенклатурного мелкосерийного производства. Основные операции, выполняемые в системе: фрезерование, растачивание, развертывание, нарезание резьбы. Заготовки подаются в приспособлениях-спутниках специальным устройством. Запас приспособлений-спутников с деталями временно хранится на складе материалов и подается на обрабатывающий центр по команде из центра управления. Применяется групповое управление станками ЭВМ. Обработанные детали снимаются со
|
|
| t |
4 6

|
Ив - |
| ЬЬ |
_ t
\ЛЛЛЛЛ*ЛЛЛЛЛЛ^.Л7УУУУУ\
|
|
| Ш Ю ESI K1 Ю Ш Ш ПЗ |
 8 \ \ 8
8 \ \ 8
|
|
Ш\ К] Ю
в
Рис. 3.27. Компоновка гибкой (переналаживаемой) системы для обработки корпусных деталей (мелкосерийное производство):
1 — погрузочно-разгрузочные станции; 2 — автоматизированный склад заготовок; 3 — кран-штабелер; 4 — автоматизированный склад готовых деталей; 5 — устройство для демонтажа приспособлений-спутников с деталями; 6 — промежуточный склад приспособлений-спутников и деталей; 7 — фрезерные станки с программным управлением; 8 — обрабатывающие центры; 9 — автоматическая транспортная тележка с блоком памяти; 10 — устройство для закрепления и установки деталей в приспособления-спутники
121
спугников на линии демонтажа и автоматически помещаются на складе готовых деталей.
Во вторую группу входят специализированные АПС для обработки или сборки небольшой группы конструктивно однородных изделий с незначительными отличиями в элементах конструкции и способах их соединения в условиях крупносерийного производства. Номенклатура изготавливаемых изделий в данном случае стабильна и, как правило, известна при создании системы. В состав таких АПС могут включаться специализированное обрабатывающее и сборочное оборудование, агрегатные многошпиндельные станки с ЧПУ, оборудование, оснащенное много-шпиндельными насадками. Передача деталей между станками при последовательной обработке может осуществляться с помощью конвейера, а загрузка-разгрузка оборудования — манипулятором с механическим приводом. Каждый станок системы стремятся спроектировать таким образом, чтобы обеспечивалось условие
К третьей группе относятся широкоуниверсальные АПС, предназначенные для обработки мелких серий разнородных деталей с изменяющейся номенклатурой.
Такие системы должны обеспечивать возможность перехода на производство новых деталей без остановки производства, снижение затрат на технологическую оснастку, сохранение работоспособности при частичном выходе из строя оборудования и высокую степень загрузки оборудования. Поэтому в этих АПС применяют, как правило, однотипные станки с широкими технологическими возможностями.
В состав АЦ как АПС более высокого уровня организационной структуры производства входят АЛ и (или) АУ, предназначенные для изготовления изделий заданной номенклатуры. Эта номенклатура значительно шире, чем номенклатура изделий, изготавливаемых на отдельных АЛ и АУ, что и является основной причиной объединения переналаживаемых автоматизированных линий и участков в общую цеховую структуру. Графически это объединение представляют в виде компоновочного плана (схемы) цеха, на основе которого в дальнейшем разрабатывают планировку оборудования. Назначение компоновочного плана — взаимная увязка входящих в состав цеха линий, участков, отделений, выбор оптимального направлении производственного процесса с кратчайшими путями перемещения объектов и средств производства, рациональными схемами материальных и информационных потоков.
Компоновочные схемы АПС неразрывно связаны с принятой формой организации производства и общим потоком производственного процесса в цехе. Так как АУ и АЛ представляют собой автономные производственно-технологические АПС и организационно-технические структуры (ОТС), объединяющим фактором
122
10 11
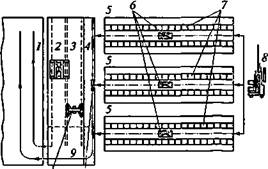
Рис. 3.28. Принципиальная схема организации серийного производства с использованием автоматизированной транспортно-накопительной системы ОРГ-3:
/ — сборочный цех; 2 — комплектовочный кран; 3 — склад готовых деталей; 4 — участок контроля; 5 — линии механической обработки; 6 — краны-операторы с автоматическим адресованием; 7 — сборно-разборные стеллажи; 8 — электро-штабелер; 9 — площадка приема, комплектации и выдачи; 10 — кран-штабелер; // — электрогрузовоз с прицепной тележкой
для них является наличие единой транспортно-складскои системы (как правило, АТСС) и автоматизированной системы организационно-технологического управления (АСУОТ). При определении состава АЦ механической обработки и сборки решающее требование сводится к обеспечению законченного цикла изготовления изделий заданных номенклатуры и объема.
В механических цехах многономенклатурного мелкосерийного производства с преобладанием предметно-замкнутых участков предусматривают их расположение в соответствии с принятой структурой транспортно-складскои системы; состав входящих в цех участков определяется видом и характером производства. Для сборочных цехов мелко- и среднесерийного производства характерно разделение на узловую и общую сборку со специализацией автоматизированных рабочих мест (крупные, средние, мелкие узлы и т.д.).
В механосборочных цехах средне- и крупносерийного производства, для которых характерны поточные линии разных типов (в том числе и автоматизированные), принято их расположение вдоль пролетов цеха, а позиций сборки (общей и узловой) перпендикулярно направлениям потоков линий механической обработки. По этому принципу организовано серийное производство изделий с применением автоматизированных транспортно-складских (АТСС) и транспортно-накопительных (АТНС) систем — соответственно типов ОРГ-2 и ОРГ-3. Принципиальная схема организации автоматизированного производства с применением АТНС ОРГ-3 приведена на рис. 3.28.
123
Контрольные вопросы
1. Какое оборудование может быть использовано для создания автоматизированных производственных систем?
2. Какие виды автоматизированных линий возможны к применению в разных типах производства?
3. Чем отличаются промышленные роботы ПР от автооператоров?
4. Какие условия учитываются при выборе ПР?
5. В чем заключается методика построения циклограмм функционирования роботов и роботизированных комплексов?
6. Для чего предназначены магазинные и бункерные загрузочные устройства? Каковы их различия?
7. Какие виды транспортных устройств используются в АПС?
8. Что входит в состав технических средств автоматизированных транспортных систем?
9. Какие виды складов используются в условиях автоматизированного производства?
10. Для чего необходимо кодирование инструментов на многооперационных станках с ЧПУ?
11. В чем смысл иодналадки инструмента на станке?
12. Что такое приспособления-спутники? Для чего они предназначены?
13. Какие задачи решаются при подготовке управляющих программ для сборочных и подвижных роботов?
14. Что является особенностью ПдР легкого класса?
15. Чем характеризуется организованная среда при использовании ПдР?
16. Охарактеризуйте три основные группы компоновочных схем АПС.
17. Назовите формы организации производства в АПС.
Глава 4
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ В ТЕХНОЛОГИЧЕСКИХ СИСТЕМАХ
4.1. Требования к математическим моделям и их классификация
Под математической моделью (ММ) технологического процесса и его элементов понимают систему математических соотношений, описывающих с требуемой точностью изучаемый объект и его поведение в производственных условиях. При построении математических моделей используют различные математические средства описания объекта — теорию множеств, теорию графов, теорию вероятностей, математическую логику, математическое программирование, дифференциальные или интегральные уравнения и др.
К. математическим моделям предъявляют требования высокой точности, экономичности и универсальности. Экономичность математических моделей определяется затратами машинного времени (работы ЭВМ). Степень универсальности математических моделей определяется возможностью их использования для анализа большего числа технологических процессов и их элементов. Требования к точности, экономичности и степени универсальности математических моделей противоречивы, поэтому разработчики находят компромиссное решение.
Степень универсальности ММ характеризует полноту отображения в модели свойств реального объекта. Однако ММ отражает лишь некоторые свойства обч>екта. Так, большинство ММ используется при функциональном проектировании, например, для нахождения оптимальных режимов резания или при расчете производительности и др. При этом не всегда требуется, чтобы ММ описывала все свойства объекта, включая, например, геометрическую форму составляющих его элементов.
Точность ММ оценивается степенью совпадения значений параметров реального объекта и значений тех же параметров, рассчитанных с помощью оцениваемой ММ. Пусть отражаемые в ММ свойства оцениваются вектором выходных параметров Y = (уи у2, ..., ут). Тогда, обозначив истинное и рассчитанное с помощью ММ значения у'-го выходного параметра через уКС1] и yMJ - соответственно, определим относительную погрешность е7 расчета параметра yj как
_ Уму ~ Учету
j ~
Учет!
125
Получена векторная оценка е^ = (е1? е2,..., гт). При необходимости сведения этой оценки к скалярной используют какую-либо норму вектора £у, например
Адекватность ММ — способность отображать заданные свойства объекта с погрешностью не выше заданной. Поскольку выходные параметры являются функциями векторов параметров внешних Q и внутренних Л'погрешность е, зависит от значений Q и X . Обычно значения внутренних параметров ММ определяют из условия минимизации погрешности гт в некоторой точке QH 0 M пространства внешних переменных и используют модель с рассчитанным вектором Л'при разных значениях Q . При этом, как правило, адекватность модели имеет место лишь в ограниченной области изменения внешних переменных — области адекватности (ОА) математической модели
OA ={ Q \ eM < b },
где 5 > 0 — заданная константа, равная предельно допустимой погрешности модели.
Экономичность ММ характеризуется затратами вычислительных ресурсов (машинных времени Ты и памяти /7М) на ее реализацию.
Математические модели имеют классификационные признаки, которые определяют их тип. Для использования их в САПР требуется знать характер отображаемых свойств объекта. В нашем случае объектом будет технологический процесс и его элементы.
Рассматривая классификационные признаки в первую очередь следует отметить, что по характеру отображаемых свойств объекта ММ делятся на структурные и функциональные.
Структурные ММ предназначены для отображения структурных свойств объекта. Различают структурные ММ топологические и геометрические. Описание математических соотношений на уровнях структурных, логических и количественных свойств принимает конкретные формы в условиях определенного объекта. Например, множество параметров, влияющих на выбор скорости резания при разных методах обработки, можно представить в виде
Mv={T „,m, t,s,d, В , rvl (4-1)
где Тк — стойкость инструмента, мин; m — показатель относительной стойкости инструмента; / — глубина резания, мм; 5 — подача, мм/об (мм/зуб, мм/2х, мм/мин); d — диаметр обрабатываемой поверхности или диаметр инструмента, мм; В — ширина обрабатываемой поверхности, мм; с„— коэффициент, характеризующий условия обработки; kv — поправочный коэффициент на скорость резания; х„ yv , zv , rv — показатели степени соответственно параметров t , s , с/и В.
126
Логические соотношения между приведенными ранее параметрами и скоростью резания v имеют вид
v = Т„ л от л cv л kv [( J л xv ) v (5 л yv ) v ( d л z„) v (5 л г„)], (4.2)
причем параметры Ти, от, с„и Аг„ всегда истинны, а истинные значения других переменных зависят от метода обработки резанием.
Формулы количественных соотношений между параметрами с учетом истинности их логических значений имеют вид:
при наружном точении
v = Cvkv ; (4.3)
при сверлении
v = "Г"" (4.4)
и т.д. Следовательно, формулы (4.1)—(4.4) представляют собой математические модели расчета скорости резания на разных уровнях абстрагирования.
Функциональные ММ предназначены для отображения физических или информационных процессов, протекающих в технологических системах при их функционировании, и обычно представляются системой уравнений, описывающих фазовые переменные, внутренние, внешние и выходные параметры.
При рассмотрении иерархических уровней ММ будут представлять собой модели на микроуровне, макроуровне и метауровне. Особенностью ММ на микроуровне является отображение физических процессов в непрерывных пространстве и времени. С помощью дифференциальных уравнений в частных производных рассчитываются поля механических напряжений и деформаций.
На макроуровне используют укрупненную дискретизацию пространства по функциональному признаку, что приводит к представлению ММ на этом уровне в виде обыкновенных дифференциальных уравнений (ОДУ). В этих моделях имеются две группы переменных — непрерывных независимых (время) и зависимых, или фазовых (такими переменными являются сила и скорость перемещения в механических системах, напряжение и сила тока в электрических системах и т. п.).
Магматические модели на метауровне описывают укруп-ненно рассматриваемые объекты (технологические системы и т. п.). В качестве математического аппарата в этом случае наряду с ОДУ используют теорию массового обслуживания, элементы дискретной математики (сети Петри и т.д.).
Теоретические модели строят на основании изучения закономерностей процессов. В отличие от формальных моделей (например, эмпирических, описывающих режимы резания) они в боль-
127
шинстве случаев более универсальны и справедливы для широких диапазонов изменения технологических параметров. Теоретические модели могут быть линейными и нелинейными, а в зависимости от мощности множества значений переменных — непрерывными и дискретными. При технологическом проектировании наиболее распространены дискретные модели, переменные которых являются дискретными величинами, а множество решений счетно. Различают также модели динамические и статические. В большинстве случаев проектирования технологических процессов используют статические модели, уравнения которых не учитывают инерционность процессов в объекте.
Различают ММ нескольких типов. В полной ММ учитываются связи всех элементов проектируемого объекта, например, маршрутная технология. Укрупненные м а к р о ММ отображают значительно меньшее число межэлементных связей. Аналитические ММ представляют собой функциональные модели (теоретические или эмпирические) и, как правило, используются при параметрической оптимизации технологических процессов. Алгоритмическая ММ представляется в виде алгоритма. Наконец, имитационная модель является алгоритмической, отражающей поведение исследуемого объекта во времени при заданных внешних воздействиях на объект (например, процесс подготовки управляющих программ для роботизированной сборки).
Выбор типа математического моделирования, наиболее эффективного в условиях конкретной задачи, определяется ее технологической основой, формой представления исходной технологической информации, общей целью исследования. Функциональную ММ в общем виде можно представить следующим образом:
F = f { X , Y ),
где X — управляемые переменные; Y— неуправляемые переменные; F— ожидаемая эффективность.
Ограничения, входящие в модель, имеют вид <р(Х, Y ) = 0. Решения на модели получаются путем определения значения X (как функции от Y ), максимизирующего (минимизирующего) F .
В зависимости от сложности задачи используются различные принципы построения моделей. Зачастую возникает необходимость разработки менее точной модели, которая оказывается более продуктивной для практики. Неизбежно решение задач, с одной стороны, разработки модели, с помощью которой проще всего получать численное решение, а с другой, обеспечения максимально возможной точности модели. Для упрощения модели используются исключение переменных, изменение характера переменных, изменение функциональных соотношений между переменными (например, применение линейной аппроксимации), изменение ограничений (их модификация, постепенный ввод ограничений в условие задачи). Мо-
128
дели, являясь эффективным средством исследования структуры задачи, позволяют обнаружить принципиально новые стратегии.
В общем случае процедура получения математических моделей элементов включает в себя следующие операции.
1. Выбор свойств объекта, которые подлежат отражению в модели. Этот выбор основан на анализе возможных применений модели и определяет степень универсальности ММ.
2. Сбор исходной информации о выбранных свойствах объекта. Источниками сведений могут быть опыт и знания инженера, разрабатывающего модель, научно-техническая литература, прежде всего справочная, описания прототипов — имеющихся ММ для элементов, близких по своим свойствам к исследуемому, результаты экспериментальных измерений параметров и т. п.
3. Синтез структуры ММ. (Структура ММ —общий вид математических соотношений модели без конкретизации числовых значений фигурирующих в них параметров. Структура модели может быть представлена также в графической форме, например в виде эквивалентной схемы или графа. Синтез структуры — наиболее ответственная и с наибольшим трудом поддающаяся формализации операция.)
4. Расчет числовых значений параметров ММ. Эта задача ставится как задача минимизации погрешности модели заданной структуры.
5. Оценка точности и адекватности ММ. Для оценки точности должны использоваться значения yHCrJ , которые не фигурировали при решении задачи.
Реализация функциональных ММ на ЭВМ подразумевает выбор численного метода решения уравнений и преобразование уравнений в соответствии с особенностями выбранного метода. Конечная цель преобразований — получение рабочей программы анализа в виде последовательности элементарных действий, реализуемых командами ЭВМ. Все указанные преобразования исходной ММ в последовательность элементарных действий ЭВМ выполняет автоматически по специальным программам, создаваемым инженером-разработчиком САПР. Инженер-пользователь САПР должен лишь указать, какие программы из имеющихся он хочет использовать. Процесс преобразований ММ, относящихся к разным иерархическим уровням, иллюстрирует рис. 4.1.
Инженер-пользователь задает исходную информацию об анализируемом объекте и о проектных процедурах, подлежащих выполнению, на удобном для него проблемно-ориентированном языке программного комплекса. Ветвь / на рис. 4.1 соответствует постановке относящейся к микроуровню задачи как краевой чаще всего в виде дифференциального уравнения с частными производными ДУЧП. Численные методы решения ДУЧП основаны на дискретизации переменных и алгебраизации задачи. Дискретизация заключается в замене непрерывных переменных конечным множе-
| Микроуровень | Макроуровень | Метауровень | ||||||||
| " | 1 | 8 | HL, | |||||||
| ДУЧП | 3 | ОДУ |
| // | ||||||
|
| ||||||||||
| 2 | 4^^ |
|
| 9 • |
| |||||
| ' |
| Специфические модели | ||||||||
| АУ | *< 6 | —*- | ЛАУ |
| ||||||
| 5 " | • | 7 |
| \ п ♦ | ||||||
| Последовательность элементарных операций | ||||||||||
Рис. 4.1. Процесс преобразования математических моделей:
1 —12 — взаимно-направленные пути дискретизации переменных в математических моделях; ДУЧП — дифференциальные уравнении с частными производными; ОДУ — обыкновенные дифференциальные уравнения; АУ — алгебраические уравнения; ЛАУ — линейные алгебраические уравнения
ством их значений в заданных для исследования пространственном и временном интервалах; алгебраизация —в замене производных алгебраическими соотношениями.
4.2. Структурные модели
Структурные или структурно-логические модели согласно ГОСТ 14.416—83 подразделяются на табличные, сетевые и перестановочные, которые определяются строками булевой матрицы:
[S,xF(S)] =
| FG | F „ | F, | Fa | Si |
| 1 | 1 | 1 | Si | |
| 1 | 1 | 0 | s7 | |
| 1 | 0 | 1 | s3 | |
| 1 | 0 | 0 | s4 | |
| 0 | 1 | 0 | s, | |
| 0 | 0 | 0 | St | |
| 0 | 1 | 1 | 1 | Sy |
| 0 | 1 | 1 | 0 | s « |
| 0 | 1 | 0 | 1 | s9 |
| 0 | I | 0 | 0 | S\a |
| 0 | 0 | 1 | 0 | Su |
| 0 | 0 | 0 | 0 | sl7 |
(4.5)
где Sj — свойства моделей, влияющие на содержание проектирования; F ( S ) — набор свойств; FG — набор свойств (если все графы объектов Ак, проектируемых по данной модели, суть простые
130
пути или цепи, Fc = 1; в противном случае Fc - 0); F „ — набор свойств, учитывающих число элементов во всех вариантах объектов Ak ( F „= 1 — число элементов о, одинаково, в противном случае F „ = 0); F \ — набор свойств, учитывающих отношения между любыми элементами объекта с, во всех вариантах объектов Ак { F ^ = 1 — отношение не меняется, в противном случае Fx= 0); Fa — набор свойств, учитывающих состав элементов а, в объектах Ак ( Fa — I — состав одинаков, в противном случае Fa = 0).
В матрице (4.5) модели класса S \ называют табличными. В табличной модели каждому набору свойств F [ Ak ) соответствует единственный вариант проектируемого объекта Ак, ьоэтому табличные модели используют для поиска стандартных, типовых или готовых проектных решений. Модели остальных классов ( S 2 ,..-, Si 2 ) применяют для получения типовых, унифицированных и индивидуальных проектных решений при наличии их вариантов и необходимости оптимизации решения. Модели классов Бъ S 5 , S 7 , Ss и Sn называют сетевыми. Структура элементов сетевой модели описывается ориентированным графом, не имеющим ориентированных циклов. В этой модели может содержаться несколько вариантов проектируемого объекта Ак, однако во всех вариантах сохраняется неизменным соотношение порядка между входящими элементами. Модели классов 53. •$»> $6, &>, «S"ioи Sl 2 называют перестановоч-н ы м и. Соотношение порядка между элементами проектируемого объекта Ак в перестановочных объектах обычно задается с помощью фафа, содержащего ориентировочные циклы, причем все варианты объектов Ак, проектируемые по перестановочным моделям, различаются порядком между элементами, входящими в них.
Объектом проектирования Ак может быть технологический процесс, операция или технологический переход.
Если рассматривать технологический процесс в качестве объекта проектирования, то операции будут элементами. При проектировании операции элементами буду! технологические переходы.
Если Акдолжен содержать фиксированный набор элементов а,е Ак,то
л
Ак = С ( л а 2 л ... л а , л ... л а„ = А я ,;
/=|
если Ак может содержать любой э л е м е н т я, е Ль то
л
Ак = flivfl2v ... v Qj v ... v a„ = V я,.
<=!
Наконец, если Ак содержит какой-либо единственный элемент я,е Ак, то
л
Ак = a{Va2V... Va,V... Va„= V«,-
5*
131

|
|
|
F2
/ Ь
| t, | F, |
| */ |
R,- | |||||||||
| \F~i | ^2 | *> | FA | F5 | F6 | F7 | F* | Ff | Fi | n | |||
| *l | Л | *> | 1 | 1 | 1 | ||||||||
| *2 | 1 | *2 | 1 | 1 | 1 | ||||||||
| T 3 | 1 | *3 | I | 1 | |||||||||
| *4 | \ | 4 | 1 | 1 | 1 | ||||||||
| *5 | I | *5 | I | ||||||||||
| 4 | 1 | Ч | 1 | ||||||||||
| t7 | \ | *7 | 1 | 1 | |||||||||
| 4 | 1 | *8 | 1 | 1 | 1 | ||||||||
Рис. 4.2. Табличные модели проектирования маршрута обработки на прутковом автомате:
а, б, е — эскизы деталей с разным набором свойств F ,; Ft — Fg — набор свойств деталей (особенности конструктивных элементов); Ff — Fj — совокупности свойств деталей; т, — операторы (технологические переходы); г, — подрезка торцов; т2, т3, г7 — обтачивание поверхностей; г4 — сверление отверстия; г5 — зенкерование; т6 — снятие фаски в отверстии; тя — отрезка
Здесь приведены табличная, сетевая и перестановочная модели. При обработке группы деталей (рис. 4.2, а—в) на токарном прутковом автомате с помощью табличных моделей (рис. 4.2, г, д) устанавливается последовательность обработки поверхностей. Каждая деталь имеет поверхности Fu ..., Fs с определенными свойствами, для группового описания которых используется выражение следующего вида:
НА) = (/', л /2 л /-4 л Fg ) v /-J v /5 v F 6 v F 7 .
Если ввести совокупность свойств более высокого уровня, например, F { = { Fu 7*2, /4, Fs ], TO получим
F\A) = F{v F3 v F5v F6v F7y
а если ввести совокупности свойств для деталей 1-, 2-, 3-й групп (соответственно для элементов аи а2, а} группы А деталей, т.е. а{,
132
|
S 5 |
| feK 1 |
Рис. 4.3. Сетевая модель операторов (операций) технологического маршрута изготовления зубчатого колеса:
| ^^3^ |
| r-^V.\Vf| |
| F2' a |
| У | Fi | ||
| Fi | Fi | ^3 | |
| tl | 1 | 1 | |
| *2 | I | 1 | |
| T3 | 1 | 1 | |
| и | 1 | 1 | |
| *5 | I | 1 | |
| *6 | 1 | 1 | |
| T7 | 1 | ||
| 4 | 1 | ||
| T 9 | |||
| TlO | 1 | ||
| *11 | 1 | 1 | |
| Tl2 | Tl | 1 | |
а — эскиз зубчатого колеса; б— матрица операторов т, (операций); в — взаимосвязи операторов (операций); Fu Рг, F } — поверхности зубчатого колеса с определенными свойствами ( F , — отверстие; F 2 — торцевые поверхности; F 3 — зубчатый профиль); т( — штамповка заготовки; х2 — протягивание отверстия и шпоночного паза; т3 — черновое обтачивание зубчатого колеса; т4 — чистовое обтачивание зубчатого колеса; х5 — нарезание зубчатого профиля; г6 — шевингование зубчатого профиля; т7 — термическая обработка; т8 — отделка базового отверстия; х<) — шлифование зубчатого профиля; тю — протирка зубчатого профиля; тп — мойка; т,2 — контроль
аъ аъ е A) /j"= F(a{) = [Fu F2, F3, F4,
Fs, F6, F7, Fg}, П = F(a2) = {/J, F2,
Ft, F4, F,, Fs}, F'{ = F(a3) = {F „ F2,
F4, Fg}, то получим
F"(A) = F{'V Fi'V Fl
Табличные модели представляют собой матрицы (см. рис. 4.2, г и д), в которых г,, ..., т8 — операторы (технологические переходы при выполнении автоматной операции).
Сетевая модель включает в себя матрицу свойств детали, описание логических отношений между свойствами и граф G = (Т, С) взаимосвязи операторов {Т= {ть т2, ..., т„} и С= {Съ С2, ..., Ст) — дуги 1рафа) по возможной последовательности их использования. Например, в логической сетевой модели (рис. 4.3) класса S $( T ) — изготовление зубчатого колеса, смежность и порядок операторов (операций) заданы графом.
Проектирование технологического процесса изготовления изделия проводится на разных уровнях. Самым высоким уровнем является разработка принципиальной схемы технологического процесса, который складывается из отдельных этапов, а каждый этап может содержать одну и более операций. В данном случае оператором является этап технологического процесса. Моделирование технологических процессов разного уровня осуществляется с помощью моделей $,{Т), при этом операторам модели $,{ЗГ) более высокого уровня (этапам технологического процесса) соответствуют
133
Рис. 4.4. Граф перестановочной модели «расцеховки» при изготовлении
изделия:
операторы (цехи): р, — литейный; pj — кузнечный; pj — механический; />« — термический; р5 — сборочный; р6 — лакокрасочный; pj — испытания и упаковки
операции и переходы, входящие соответственно в маршрут и операцию, проектируемые по моделям ^(Т1) более низкого уровня. Граф перестановочной модели класса S (,( T *) расцеховки при изготовлении изделия приведен на рис. 4.4.
4.3. Математические модели на разных иерархических
уровнях
Математические модели на микроуровне
Данные модели связаны с исследованием напряженного состояния деталей конструкции и связанные с ним расчеты на прочность.
Напряженное состояние деталей конструкции в зависимости от геометрии исследуемого узла, вида приложенной нагрузки и свойств материала описывается разного вида дифференциальными уравнениями, любое из которых может быть получено из общего квазигармонического уравнения
где х, y , z — пространственные координаты; Кх, Ку, К? — коэффициенты; Q — внешнее воздействие; <р — искомая непрерывная функция.
В двухмерном случае при Кх- Ку ~ I уравнение (4.6) сводится к уравнению, описывающему напряженное состояние, возникающее в поперечном сечении упругого однородного стержня под воздействием крутящего момента М:
&%* ■**-% (4,,
где Е — модуль сдвига материала стержня; 6 — угол закручивания
на единицу длины; ф — функция, связанная с напряжениями сдвига
йф дф
тх и ту уравнениями т. = —-, т., = —-.
Ду дх
134
В уравнение (4.7) крутящий момент в явном виде не входит. С искомой функцией напряжения ср крутящий момент связан уравнением
М = 2 fq > dS , s где S — площадь рассматриваемого сечения.
Точное решение краевых задач получают только в частных случаях. Поэтому реализация таких моделей заключается в использовании различных приближенных моделей. В настоящее время наиболее широкое распространение получили модели на основе интегральных уравнений и модели на основе метода сеток.
Одним из наиболее популярных методов решения краевых задач в САПР является метод конечных элементов.
Математические модели на макроуровне
Как уже отмечалось в подразд. 4.1, технические подсистемы на макроуровне характеризуются с помощью фазовых переменных, которые образуют вектор неизвестных в ММ технической системы. В большинстве технических систем можно выделить три типа простейших элементов — технических подсистем, в частности: а) элемент типа R (элемент диссипации, т. е. рассеяния, энергии; на этом элементе, как правило, происходит преобразование энергии в тепловую); б) элемент типа С; в) элемент типа L (на элементах типа С и L происходит накопление потенциальной и кинетической энергии. Сочетанием данных простейших элементов, а также источников фазовых переменных может быть получена ММ технического объекта практически любой сложности. Для каждой физической подсистемы справедливы свои законы, однако для простейших элементов их уравнения одинаковы. Рассмотрим в качестве примера электрическую и механическую подсистемы.
Электрическая подсистема. Фазовыми переменными электрической подсистемы являются сила тока /и напряжение U . В данном случае в качестве простейших элементов рассматривают электрическое сопротивление R , электрическую емкость С и электрическую индуктивность L . Тогда компонентными уравнениями для трех типов простейших элементов являются следующие:
•уравнение электрического сопротивления (закон Ома)
• уравнение электрической емкости
135
•уравнение электрической индуктивности
и L dt '
где / — время.
Механическая поступательная система. Фазовыми переменными данной подсистемы являются сила F и скорость v — соответственно аналоги силы тока и напряжения в электрической подсистеме, а компонентными уравнениями для трех типов простейших элементов служат:
• уравнение вязкого трения
**'
где RK = l / k — аналог электрического сопротивления; к — коэффициент вязкого трения;
• уравнение массы т (уравнение второго закона Ньютона)
f = та = см ^,
где F — сила; а =------- ускорение; т = Q, — масса, являющаяся
at аналогом электрической емкости;
• уравнение пружины
F = кх,
где F— сила; к — жесткость пружины; х — перемещение.
Если продифференцировать обе части этого уравнения по вре-
aF . . AF
мени /, то получим —— = kv , откуда вычислим скорость v - Lu •—-,
где Lh = l / k — аналог электрической индуктивности.
Аналогичное компонентное уравнение можно получить из закона Гука для элемента, у которого учитывается сжимаемость, т.е.
Р= Е~, где Р — напряжение в элементе; Е — модуль Юнга; / —
длина элемента; А/ — изменение длины элемента. Умножив обе части этого уравнения на площадь S поперечного сечения злемен-
A ( PS ) ES d(A/)
та и продифференцировав по времени t , получим —-— = —--------- —;
At I at
d(A/) __ .__ AF ES . AF . I
-Jjp = v ; PS = F . Тогда — = —z\ или v = L „ —, где IM = — —
аналог электрической индуктивности.
Механическая вращательная подсистема. Фазовые переменные этой подсистемы — моменты сил М и угловые скорости со — соответственно аналоги силы тока и напряжения для электрической
136
подсистемы. Компонентными уравнениями трех типов простейших элементов в механической вращательной подсистеме являются:
• уравнение вязкого трения вращения
где Ящ,= 1 /к — аналог электрического сопротивления; к — коэффициент трения вращения;
• основное уравнение д и н а м и к и вращательного дви-
жен ия
где J — момент инерции элемента — аналог электрической емкости;
• уравнение кручения бруса с круглым поперечным сече
нием
M = GJpe ,
где М — крутящий момент; G — модуль сдвига; /р — полярный
г, d < p момент инерции сечения; 6 = -у — относительный угол закручи-
вания. Для бруса конечной длины, 6 = —, где <р — угол закручивания; / — длина бруса.
Продифференцируем обе части последнего уравнения по времени:
| AM = GJP dip At / d/' |
|
|
Если учесть, что —- = ю и Lw = -тгт ■> то можн° привести
at uJn
данное уравнение к виду
. йМ
в котором вращательная гибкость LBp — аналог электрической индуктивности.
Аналогичное компонентное уравнение можно получить для спиральной пружины, уравнение которой М = ар, где с — жесткость пружины. Продифференцировав обе части данного уравнения по
времени и выполнив преобразования, также получим ш = LHp —r—,
где Z-вр = 1/с — аналог электрической индуктивности.
Топологические уравнения в большинстве физических подсистем базируются на уравнениях равновесия и уравнениях непрерывности.
Рассмотрим аналогии топологических уравнений в, физической подсистеме по отношению к электрической подсистеме. В электри-
137
ческой подсистеме связи между отдельными элементами основываются на двух основных правилах Кирхгофа. Согласно первому правилу Кирхгофа алгебраическая сумма сил токов, сходящихся в любых узлах схемы, равна нулю, т.е. £/* =0 (уравнение рав-
н о в е с и я), где 1к — сила тока в к-й ветви; р — множество номеров ветвей, инцидентных рассматриваемому узлу.
По второму правилу Кирхгофа сумма падений напряжений Ц на элементах схемы при их обходе по произвольному контуру равна нулю, т.е. ££/,-=0 (уравнение непрерывности), где./ —
номер ветви; Ц — падение напряжения нау-й ветви схемы, входящей в контур; q ~ множество номеров ветвей, входящих в рассматриваемый контур.
В механической вращательной подсистеме аналогом уравнения
первого правила Кирхгофа является уравнение, основанное на
принципе Д'Аламбера для вращательных подсистем, а именно
2 Мк = 0, где Мк — момент силы, действующей относительно
оси вращения, включая момент, вызванный моментом инерции. Аналогом уравнения второго правила Кирхгофа является уравнение принципа сложения угловых скоростей вдоль оси вращения, т.е. £(оу = 0.
Математические модели на метауровне
Математические модели в технологических системах отражают большое разнообразие процессов. Рассмотрим некоторые из них.
Математические модели с использованием целочисленного програм мирования. Для создания технологической структуры участка из робототехнических комплексов необходимо использовать п РТК.
Для их приобретения выделен денежный фонд в сумме ./V рублей. Стоимость одного РТКу'-го типа Су, а его производительность о, (у = 1, п). Требуется выбрать РТК, обеспечивающие максимальную суммарную производительность в пределах установленного денежного лимита N.
Математическая модель данной операции:
я
F ( x ) = max ^ ajXj ;
ZCjXj < N \
_ fl, если РТК приобретается; J [0, в противном случае,
где х = (jc,, х2, ..., Xj , ..., х„); с,> 0; Cj > 0; А' > 0 — целые числа.
Проведем решение методом ветвей и границ. Если отбросить требование целочисленности, то переменные ар Cj будут
138
изменяться непрерывно на отрезке [0, 1]. Решение такой непрерывной задачи будет верхней границей (так как определяется максимум) множества значений целевой функции на соответствующем подмножестве решения.
Алгоритм решения непрерывной задачи состоит в следующем. Упорядочим коэффициенты а1г а2,..., о,-,..., а„ в порядке убывания величин Kj = Oj / Cj и соответственно этому порядку пронумеруем переменные и параметры задачи.
Процедура разбиения (методом ветвей и границ) допустимого множества G , задаваемого ограничениями, заключается в следующем. Разбиваем G на два подмножества Ct и G 2 , из которых первому принадлежат все решения с х, = I, а второму — с х^ = 0. Далее каждое из подмножеств С, и G2 опять разбивают на два, в первом
ИЗ КОТОРЫХ X , = 1, ВО ВТОРОМ X ] = 0, И Т.Д.
На каждом шаге очередного разбиения выбирают подмножество, которому соответствует максимальное значение оценки. Поиск решения заканчивают, если на некотором шаге получают допустимое решение значения целевой функции, на котором шаг будет наибольшим по сравнению с оценками для всех подмножеств — кандидатов на разбиение.
Рассмотрим численный пример. Пусть целевая функция и ограничение имеют следующий вид:
/(х) = (6х! + 8х2+ 10х3+ 11х4+ 9х5) -» max;
2х, + Зх2 + 7х3 + 10х4 + 9х5 < 20.
В данной задаче
|
|
А = (а„ аъ а3, ал, с5) = (6, 8,10,11,9);
С=(СЬ Cj, С3, Сц, С5) =
= (2,3,7, 10, 9);W=20.
Таким образом, предлагаются пять типов РТК, т.е. п - 5. Схема решения (т.е. схема разбиения) показана на рис. 4.5.
| Рис. 4.5. Схема решения задачи создания структуры участка из роботизированных технлогичес-ких комплексов метолом ветвей и границ: Х\, хъ д"з, X) — операторы |
При х, = 1 получим /(х) = 32,8. Имеем верхнюю оценку. Тогда для х2, ..., х5 отказываемся от целочисленное™, изменяя Xj (У = 2, 3,4, 5) на отрезке 10, 1] непрерывно. При X, = 0 соответственноДх) = 29, причем решение непрерывной задачи X! =0, х2 = х3=х4 = 1, Х5 = 0 является целочисленным (на рис. 4.5 такие подмножества отмечены двойными кружками).
139
Выбираем подмножество ху = 1. Для варианта xt = I, х2 = 1 получим/(х) = 32,8, а при х2 = 0 — 27,8. Выбираем xi = I и х2 = 1. При х3 = 1 все остальные Ху (у = 4, 5) должны быть нулями, так как в противном случае нарушится ограничение. При х3 = 0 находим/(х) -= 29,09. В итоге получаем х4 = 1, х5 = 0 и/(х) = 25, что меньше 29. Поэтому допустимое решение, полученное на первом шаге, т.е. х, = 0, х2 = х3 = Х4 = 1, х5 = 0 [ /(х) = 29], является оптимальным.
Математические модели с использованием систем массового обслу живания. Эти системы основаны на марковском случайном процессе. Физическая система S с течением времени меняет свое состояние (переходит из одного состояния в другое) случайным образом. Тогда в системе 5" протекает случайный процесс, который называется марковским, если для любого момента времени /0 вероятностные характеристики «процесса в будущем» зависят только от его состояния в данный момент времени t 0 и не зависят оттого, когда и как система пришла в это состояние. Вероятностные характеристики «процесса в будущем» можно найти, например, как вероятность того, что через некоторое время т система S окажется в состоянии 51 или сохранит состояние 5*0 и т.п. Таким образом, в марковском случайном процессе будущее зависит от прошлого только через настоящее.
Рассматривая марковские процессы с дискретными состояниями и непрерывным временем, удобно представлять себе, что все переходы системы 5 из состояния в состояние происходят под действием каких-то потоков событий (поток вызовов, поток отказов, поток восстановлений и т.д.). Если все потоки событий, переводящие систему S из состояния в состояние, простейшие, то процесс, протекающий в системе, будет марковским, так как простейший поток не обладает последействием (в нем будущее не зависит от прошлого).
Если система S находится в каком-то состоянии Sh из которого есть непосредственный переход в другое состояние 5} (стрелка, ведущая из 5} в 5) на графе состояний), то мы себе это будем представлять так, как будто на систему, пока она находится в состоянии Sh действует простейший поток событий, приводящий ее по стрелке 5,--> 5}. Как только появится первое событие этого потока, происходит «перескок» системы из 5, в 5}.
Для наглядности очень удобно представлять граф состояний.
Построим размеченный граф состояний для технического устройства из двух узлов. Состояния системы будут следующими:
50 — оба узла исправны;
5| — первый узел ремонтируется, второй исправен;
5г — второй узел ремонтируется, первый исправен;
53 — оба узла ремонтируются.
Интенсивность потоков событий, переводящих систему из состояния в состояние, будем вычислять, предполагая, что среднее время ремонта узла не зависит от того, ремонтируется один узел
140
Рис. 4.6. Размеченный граф состояний системы:
^'0, S{, Si, Sj — состояния технического устройства; Л|, Xj — интенсивности отказов узлов технического устройства; и,, ц2 — интенсивности восстановления (ремонта) узлов технического устройства
или сразу оба. Это будет именно так, если ремонтом каждого узла занят отдельный специалист. Найдем все интенсивности потоков событий, переводящих систему из состояния в состояние. Пусть система находится в состоянии S 0 . Какой поток событий переводит ее в состояние 51,? Очевидно, поток отказов первого узла. Его интенсивность X] равна единице, деленной на среднее время безотказной работы первого узла. Какой поток событий переводит систему обратно из Sj в Sf > Очевидно, поток «окончания ремонтов» первого узла. Его интенсивность щ равна единице, деленной на среднее время ремонта первого узла. Аналогично вычисляются интенсивности потоков событий, переводящих систему по всем стрелкам графа рис. 4.6. Имея в своем распоряжении размеченный граф состояний системы, легко построить математическую модель данного процесса. В самом деле, пусть рассматривается система S , имеющая п возможных состояний Sb Si , .-., Sn . Назовем вероятностью /-го состояния вероятностьp ,{ t ) того, что в момент /система будет находиться в состоянии Sh Очевидно, что для любого момента времени сумма вероятностей всех состояний равна единице:
1=1
Имея в своем распоряжении размеченный граф состояний, можно найти вероятности всех состояний системы p ^ t ) как функции времени /. Для этого составляют и решаются так называемые уравнения Колмогорова— особого вида дифференциальные уравнения, в которых неизвестными функциями являются вероятности состояний:
at
- £- = Xlp0+ \i2p3 - (k2 + ji, )px; at
-& ■ = X2p0 + ц,р3 - (Л, + \i2)p2; -&■ = X2/>, + X,/>2 - (ц, + \i2)p2,
(4.8)
141
где Ц|, ц2 ~ интенсивности восстановления (ремонта) узлов технического устройства; X,, Х2 — интенсивности отказов узлов технического устройства.
Чтобы решить уравнения Колмогорова и найти вероятности состояний />,{/), прежде всего надо задать начальные условия. Если мы точно знаем начальное состояние системы Sh то для начального момента времени, т.е. при / = 0, р,ф) = 1, а вероятности всех остальных начальных состояний системы равны нулю. Таким образом, уравнения (4.8) надо решать при следующих начальных условиях />о(0) = I, р|(0) = л(0) = р3(0) = 0 (в начальный момент оба узла исправны).
Если вероятности ри pj , рз постоянны, то их производные равны нулю. Чтобы найти финальные вероятности, нужно все левые части уравнений Колмогорова принять равными нулю и решить полученную систему уже не дифференциальных, а линейных алгебраических уравнений.
Можно и не записывать уравнений Колмогорова, а непосредственно по графу состояний написать систему линейных алгебраических уравнений. Если перенести отрицательный член каждого уравнения из правой части в левую, то получим сразу систему уравнений, где слева находится финальная вероятность данного состояния ph умноженная на суммарную интенсивность всех потоков, берущих начало из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в /-е с о с т о я н и е, на вероятности тех состояний, из которых эти потоки исходят.
Пользуясь этим правилом, напишем линейные алгебраические уравнения для финальных вероятностей состояний системы, граф состояний которой приведен на рис. 4.6:
(X, +X2)p0=iilp,+ii2p2;
(X2+Hi)/>i =^|А)+^2Л;
(4.9) (Xi + M-2)/>2 =Х2А)+ц,/?3;
(ц|+Н2)/>з = Х2р,+Х|/?2. Нормировочное условие имеет вид
Po + Pi + Pi + P )= 1. (4.10)
Процесс работы системы массового обслуживания (СМО) представляет собой случайный процесс с дискретными состояниями и непрерывным временем; состояние СМО меняется скачком в моменты появления каких-то событий (например, приход новой заявки; окончание обслуживания; момент, когда заявка по каким-либо причинам отзывается, и др.).
142
Предмет теории массового обслуживания ~ построение математических моделей, связывающих заданные условия работы СМО (число каналов, их производительность, правила работы, характер потока заявок) с интересующими нас характеристиками — показателями эффективности СМО, описывающими с той или другой точки зрения ее способность справляться с потоком заявок. В качестве таких показателей (в зависимости от обстановки и целей исследования) могут применяться разные величины, например среднее число заявок, обслуживаемых СМО в единицу времени; среднее число занятых каналов; среднее число заявок в очереди и среднее время ожидания обслуживания и т.д. Среди заданных условий работы СМО мы намеренно не выделяем элементов решения: ими могут быть, например, число каналов, их производительность, режим работы СМО и т.д.
13 качестве примера рассмотрим простейшую л-канальную СМО с отказами. Задача: имеются л каналов, на которые поступает поток заявок с интенсивностью Я. Поток обслуживании имеет интенсивность [х (величина, обратная среднему времени обслуживания t & ).
Определить параметры функционирования СМО:
Л — абсолютную пропускную способность, т.е. среднее число заявок, обслуживаемых в единицу времени;
Q — относительную пропускную способность, т. е. среднюю долю пришедших заявок, обслуживаемых системой;
Ртк — вероятность отказа, т. е. того, что заявка покинет СМО необслуженной;
к — среднее число занятых каналов.
Решение. Состояния S системы СМО будем нумеровать по числу заявок, находящихся в ней (в данном случае число заявок совпадает с числом занятых каналов):
S 0 — в СМО нет ни одной заявки;
St — в СМО находится одна заявка (один канал занят, остальные свободны);
Sk — в СМО находятся к заявок (к каналов заняты, остальные свободны);
S „ — в СМО находятся п заявок (все п каналов заняты). Граф состояний СМО (рис. 4.7) соответствует схеме гибели и размножения. Разметим этот граф, т.е. проставим у стрелок интен-
Д. А. . ■■, Л Л , ,
| So |
-::: гЕ£г:::ГЕ
Ц
Зц V—U+1)m им —
Рис. 4.7. Граф состояния СМО:
A'oi Si , S 2, ..., St , .... S „ — состояния системы СМО; X — интенсивность потока заявок; ц — интенсивность потока обслуживания
143
сивности потоков событий. Из состояния So в состояние St систему переводит поток заявок с интенсивностью X. (Как только приходит заявка, система перескакивает из So в 5\; аналогичный поток заявок переводит систему из любого левого состояния в соседнее правое — показано верхними стрелками на рис. 4.7.)
Проставим интенсивности у нижних стрелок. Пусть система находится в состоянии Si , когда работает один канал, который производит ц обслуживании в единицу времени (у стрелки 5| -» So проставлена интенсивность обслуживания ц). Допустим, что система находится в состоянии ф, т. е. работают два канала. В этом случае, чтобы системе перейти в состояние St , необходимо, чтобы было закончено обслуживание либо первым, либо вторым каналом. Суммарная интенсивность их потоков обслуживании равна 7\ l (см. у соответствующей стрелки). Суммарный поток обслуживании, даваемый тремя каналами, имеет интенсивность 3|Л, а в случае к каналов — Iqx (эти интенсивности проставлены у нижних стрелок на рис. 4.7).
Теперь, зная все интенсивности, воспользуемся формулами (4.9), (4.10) для нахождения финальных вероятностей состояния системы в схеме гибели и размножения:
. X X2 X3 X* X"
| (4.11) |
| Ро |
1 + — + —-=- + . . , + ... + . . , +... + -
| i 2 ц2 2-Зц3 '" kl \ Lk '" п\\х" j
X X2 X"
Члены разложения —, —7,...,---------------- представляют собой коэф-
ц 2jr л!|л"
фициенты при ро в выражениях для вероятностей />,, р^, ..., рп:
X X2 X* X"
ц 2\ х.г к\\хК п\\х"
Заметим, что в формулы (4.11), (4.12) интенсивности X и ц входят в виде отношения Х/ц, которое можно обозначить следующим образом:
Х/р. = р.
По смыслу величина р, называемая приведенной интенсивностью потока заявок, — это среднее число заявок, приходящее за среднее время обслуживания одной заявки. Используя данное обозначение, приведем формулы (4.11) и (4.12) к виду
( р2 р* pnV1
Л Т + р + 2!+-+* Т + - + ^!
Р\ = РА>, Рг = ^Ро,~,Рк =^ТА>..................... Р" =^р°- ^413^
Таким образом, формулы для нахождения финальных вероятностей состояний системы найдены. По ним мы вычислим харак-
144
теристики эффективности СМО. Сначала найдем Рт — вероятность того, что пришедшая заявка получит отказ, т.е. не будет обслужена. Для этого нужно, чтобы все п каналов были заняты, т.е.
Рж-Р^—.Рь- (4-14)
п\
Отсюда находим относительную пропускную способность Q — вероятность того, что заявка будет обслужена:
(2=1-/^=1-^-^0- (4.15)
Абсолютную пропускную способность А получим, умножая интенсивность потока заявок X на Q :
|
|
| A = XQ = X |
Каждый занятый канал в единицу времени обслуживает в среднем ц заявок. Следовательно, среднее число занятых каналов
* = -, (4.16)
или, учитывая формулу для А:
к = р
(4.17)
Приведенные выше положения используют, например, при выборе компоновочного решения РТК (обслуживание группы станков одним или несколькими роботами). Это дает также возможность выполнить функции транспортирования. При многостаночном обслуживании возникают условия для потерь времени или ожидания станком обслуживания, если одновременно на нескольких позициях возникает потребность в новых заготовках.
Характеристики эффективности обслуживания группы станков роботом (роботами) определяются по формулам (4.13)—(4.17).
Математические модели с использованием сетей Петри. Сети Петри являются эффективным инструментом дискретных процессов, в частности, при определении функционирования станочных систем. Особенность сетей Петри заключается в возможности отображения параллелизма, асинхронности и иерархичности процессов.
Па рис. 4.8 приводится сеть Петри, для которой /?, еР и /, е Т, где Р — конечное непустое множество позиций (состояний); Т — конечное непустое множество переходов (событий). Для систем F : РхТ—> {0, 1, 2, ...}; Н: ТхР—> {0, 1, 2, ...} — функции соответственно входных ( F ) и выходных (Н) инциденций; ^: Р -» {0, 1, 2, ...} — начальная маркировка. Вершины сети />,- е Р изображены
145
|
|
кружками, а вершины/,-е Г—черточками (баркерами). Дуги соответствуют функциям инцидентности позиций и переходов. Точки в кружочках означают заданную начальную маркировку. Число маркеров в позиции равно значению функции ц: /*-» {0, 1,2,...}. Переход от одной маркировки к другой осуществляется срабатыванием переходов. Переход / может сработать при маркировке jx, если он является возбужденным:
| Рис. 4.8. Сеть Петри: Р\—Р$ — позиции (состояния станочной системы); /, — f4 — переходы (события) при функционировании станочной системы |
ц(Р) - F ( P , /) > О, Vpe P . (4.18)
Данное условие показывает, что в каждой входной позиции перехода t число маркеров не меньше веса дуги, соединяющей эту позицию с переходом. В результате срабатывания перехода /, удовлетворяющего условию (4.18), маркировку ц заменяют маркировкой \х по следующему правилу:
Ц'0>) = V ( P ) - F ( P , О + Щ(, р), V/, t P .
По этому правилу по причине срабатывания из всех входных позиций перехода / изымают F ( p , t ) маркеров, а в каждую выходную позицию добавляют //(/, р) маркеров. Данное положение означает, что маркировка \ l ' непосредственно достижима из маркировки \ i . Функционирование сети Петри — последовательная смена маркировок в результате срабатывания возбужденных переходов.
Состояние сети в данный момент времени определяется ее текущей маркировкой. Важная характеристика сети Петри — граф достижимости, с помощью которого описываются возможные варианты функционирования сети (рис. 4.9). Такой граф имеет вершины, которые являются возможными маркировками. Маркировки ц и \ i соединяются в направлении г дугой, помеченной символами перехода / е Гили ц -^ ц'. Маркировка ц' является достижимой из маркировки р. при существовании следующей последовательности переходов: т = (/,, t 2 , ..., 4), что обеспечивает ц \ ц' -^ ... -^ »х.
В качестве примера рассматривается сеть Петри, изображенная на рис. 4.8, для которой
N = ( Р, Т, F , Н, цо), где Р= {ри ръ р^ рА, />5};
Т= {/„ /2, h , Ц, /5}; Цо = (1, 1,0,0,0).
Функции F и Н заданы следующими матрицами:
146
|
|
| (1,0,0,2,1) '* / \' з |
| (1,0,0,3,0) |

 (2,1,0,1,1)
(2,1,0,1,1)
|
|
(0,0,2,3,0) h /\ h
(2,2,1,0,0)
*\/\ ь.
Рис. 4.9. Фрагмент графа достижимости сети Петри: Л—U — переходы (события) при функционировании станочной системы
| и | h | h | и | |
| А | 1 | 0 | 0 | 0 |
| F Н | 1 | 0 | 0 | 0 |
| г — Ръ | 0 | 1 | 0 | 0 |
| Ра | 0 | 0 | 1 | 0 |
| Pi | 0 | 0 | 0 | 1 |
| Р\ | Рт. | Ръ | Ра | Ръ | |
| >1 | 0 | 0 | 1 | 2 | 0 |
| ; II = h | 1 | 0 | 0 | 0 | 1 |
| h | 1 | 1 | 0 | 0 | 0 |
| и | 0 | 0 | 0 | 1 | 0 |
Фрагмент графа достижимости для сети Петри приведен на рис. 4.9.
Сети Петри применяют для описания разных работ. Например, на рис. 4.10 показана сеть Петри для работы группы металлорежущих станков, обслуживаемых одним роботом. Переходы связаны с определенными событиями работы РТК: tx — поступление запроса (заявка от станка) на использование робота, например, для его загрузки заготовкой; t 2 — робот занят; /3 — освобождение робота; /4 — выход обслуженной заявки. Позиции pt характеризуют состояние обслуживающего робота. Позиция р4 используется для отображения состояния робота. Если в />4 имеется метка, то робот свободен и пришедшая заявка от станка вызывает срабатывание перехода t 2 . Пока заявка не будет обслужена, метки в р4 не будет и при-
Рис. 4.10. Пример сети Петри для описания работы роботизированного технологического комплекса: Pi — Pt — позиции (рабочие состояния) РТК; /| —/4 — переходы (события) при функционировании РТК
гМЭгГ*® '£г©~^
J < D -
147
шедшие в позицию />j запросы вынуждены ожидать срабатывания перехода /3.
Дата: 2018-12-28, просмотров: 429.