В аксиоматической теории вычитание натуральных чисел было оп­ределено как операция, обратная сложению:

а - b = с <=> ($ÎN) b + с = a

Вычитание целых неотрицательных чисел определяется аналогично. Выясним, каков смысл разности таких чисел, если а = n(А), b = n(В) .

Теорема 3. Пусть А - конечное множество и В - его собственное подмножество. Тогда множество А\В - тоже конечно, причем выпол­няется равенство n(А\В)  =  n(А) - n(В)

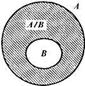
Рис. 112

Доказательство. Так как по условию В - соб­ственное подмножество множества А, то с помощью кругов Эйлера их можно представить так, как на рисунке 112. Разность А\В на этом  рисунке за­штрихована. Видим, что множества В и А\В не пересекаются и их объединение равно А. Поэтому число элементов в множестве А можно найти по формуле n(А) = n(В)  + n(А\В), откуда, по определению вычитания как операции, обратной сложению, получаем, что n(А\В)  =  n(А) - n(В).

Из рассмотренной теоремы следует, что с теоретико-множествен­ных позиций разность натуральных чисел а  и b представляет собой число элементов в дополнении множества В до множества А, если а = n(А), b = n(В) и ВÌА.

а – b = n (А) - n (В) = n (А\В) , если В Ì А.

Аналогичное истолкование получает вычитание нуля, а также вычитание а из а.

Так как А \  Æ = А, А \ А = Æ, то а - 0 = а  и а - а = 0.

Взаимосвязь вычитания чисел и вычитания множеств позволяет обосновать  выбор действия при решении текстовых задач. Выясним, например, почему следующая задача решается при помощи вычитания : «У школы росло 7 деревьев, из них 4 березы, остальные липы.  Сколько лип росло у школы?»

В  задаче рассматриваются три множества: множество А всех деревьев, множество В берез, оно является подмножеством множества А; и множество  С лип - оно представляет собой дополнение множества В до А. В задаче требуется найти число элементов в этом дополнении.

Так как по условию n(А) = 7, n(В) = 4 и ВÌА, то n(С) = n(А\В) =  n(А) - n(В)  = 7 – 4.

Разность 7 - 4 - это математическая модель данной задачи. Вычислив значение этого выражения, получим ответ на вопрос задачи: 7 -- 4 = 3. Следовательно, у школы росло 3 липы.

Рассматриваемый подход к сложению и вычитанию целых неотрицательных чисел позволяет истолковать с теоретико-множественных позиций правила вычитания числа из суммы и суммы из числа.

Выясним, например, теоретико-множественный смысл правила: «Если а. b, с - натуральные числа и а > с, то (а + b ) - с = (а - с) + b».

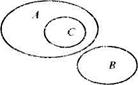
Пусть А, В и С - такие множества, n(А) = а, n(В) = b и А Ç В = Æ, СÌА  (рис. 113). Нетрудно доказать, что для данных множеств А, В имеет место равенство (А È В) \ С = (А\С) È В.

Но n( (А È В) \ С) = n (А È В) – n(С) = (а + b ) – с, а n((А\С) È В) = n(А\С) + n(В) – (а – с) + b.

И следовательно (а + b ) - с = (а - с) + b

С теоретико-множественной позиции можно рассмотреть и смысл отношений «больше на» и  «меньше на».

В аксиоматической теории определение отношения «меньше на» («больше на») естественным образом вытекает из определения отношения «меньше». Действительно, из того, что а < b  тогда и только тогда, когда существует  такое натуральное число с, что а + с = b, имеем,  что «а меньше b  на с» или «b  больше а на с».

Если n(А) = а, n(В) = b и установлено, а < b , то. исходя из теоретико-множественного смысла отношения «меньше», в множестве В можно выделить собственное подмножество В₁, равномощное множеству А, и непустое множество В\В₁. Если число элементов в множестве В\В₁. обозначить через с (с ¹ 0), то в множестве В будет столько же элементов, сколько их в А, и еще с элементов:

n(В) = n(В) + n(В\ В₁.) или b = а + с,  что означает, что «а меньше b  на с» (или «больше а на с»). Итак, с теоретико-множественной точки зрения «а меньше b на с» (или «b больше а на с») означает, что если n(А) = а, n(В) = b, то в множестве В содержится столько элементов, сколько их в А, и еще с элементов.

Так как с= п(В\В₁). где В₁ Ì В, n(В) = b, n(В₁) = а, то, по опреде­лению разности, с = а - b. Следовательно, чтобы узнать, на сколько одно число меньше или больше другого, надо из большего числа вы­честь меньшее.

Взаимосвязь действии над множествами с действиями над числами, теоретико-множественный смысл отношений «меньше на» и «больше на» позволяют обосновывать выбор действий при решении задач с этими отношениями.

Рассмотрим, например, такую задачу: «На столе 5 чашек, а ложек на 2 больше. Сколько на столе ложек?» Легко видеть, что она решает­ся при помощи сложения. Почему?

В задаче речь идет о двух множествах: множестве чашек (А) и мно­жестве ложек (В). Известно, что в первом множестве 5 элементов, т.е. п(А) = 5. Число элементов во втором множестве требуется найти при условии, что в нем на 2 элемента больше, чем в первом. Отношение «больше на 2» означает, что в множестве В элементов столько же, сколько их в А. и еще 2 элемента (рис. 114). Применимо к тем множе­ствам, о которых идет речь в задаче, это означает, что ложек на столе столько же, сколько чашек, и еще 2. Используя правило подсчета элементов в объединении непересекающихся множеств, получаем: п(В) = п(В₁) + п( В\ В ₁ ) =5+2. Так как 5 + 2 = 7, то получим ответ на вопрос задачи: на столе 7 ложек.

О О О О   О

Х Х Х Х Х Х Х

Рис. 114

Рассмотрим еще одну задачу: «На столе 5 чашек, а ложек на 2 меньше. Сколько на столе ложек?» Выясним, почему она решается при помощи вычитания.

В задаче речь идет о двух множествах: множестве чашек (А) и мно­жестве ложек (В). Известно, что в первом множестве 5 элементов, n (А)= 5. Число элементов во втором множестве надо найти при условии, что в нем на 2 элемента меньше, чем в первом. Отношение меньше на 2» означает, что в множестве В элементов столько же, сколько их в А, но без двух (рис. 115). Применимо к тем множествам, о которых идет речь в задаче, это означает, что ложек на столе столько же, сколько чашек, но без двух. Таким образом, п(А) = п(А\А₁) = 5 - 2. Так как 5-2=3, то получим ответ на вопрос  задачи: на столе 3 ложки.

О О О О О

Х Х Х  

Рис. 115

Упражнения

1.       Объясните с теоретико-множественной точки зрения смысл выражений:

а) 8-3;   6)4-4;      в) 4 - 0.

2..      Объясните, почему нижеприведенные задачи решаются при помощи вычитания.

а) В корзине было 7 морковок, 3 из них отдали кроликам. Сколько морковок осталось?

б) На столе 8 чашек, их на 3 больше, чем стаканов. Сколько стаканов на столе?

в) На верхней полке шкафа 7 книг, а на нижней 4. На сколько книг больше на верхней полке, чем на нижней?

3. Обоснуйте выбор действий при решении задач.

а) На одной полке 5 книг, на другой на 3 больше. Сколько книг на двух  полках?

б) Во дворе гуляли 6 мальчиков, а девочек на 2 меньше. Сколько  детей гуляло во дворе?

4. Запишите, используя символы, правило вычитания суммы из числа и дайте его теоретико-множественное истолкование.

Лекция 37. Произведение и частное  целых неотрицательных чисел

Определение произведения, его существование и единственность. Законы умножения. Определение произведения через сумму.

Определение частного целого неотрицательного числа на натуральное, его существование и единственность. Теоретико-множественный смысл правил деления суммы и произведения на число.