Рис. 69 - Пространственная модель
| Схема решения задачи: 1. Построение осуществляют по алгоритму 1-ой позиционной задачи. 2. Плоскость S, проходящая через прямую n , пересечет сферу по окружности d. Искомые точки М и N – результат пересечения окружности d с прямой n . |
Если заключение прямой в проецирующую плоскость не приводит к простому решению, то применяют один из способов преобразования чертежа, чтобы проекции линии пересечения сферы с введенной плоскостью были бы графически простыми (дуга окружности или прямая).
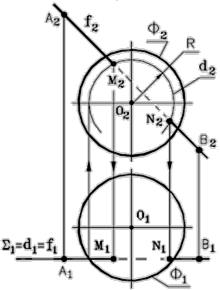Рис. 70 - Комплексный чертеж
| Рассмотрим пример: Определить точки М и N пересечения фронтали f ( AB ) со сферой Ф, (рис. 70). Анализ решения: - окружность d ( R ) сечения сферы Ф плоскостью S çç П2 , проходящей через f, спроецируется на П2 без искажения. Построение: 1. Через прямую f проводим фронтальную плоскость уровня S: S çç П2 . 2. Определяем фронтальную проекцию окружности: S Ç f = d ( R ) . |
3. Определяем фронтальные проекции искомых точек: М2 Ù N 2 = d 2 Ç f 2 ( А2 В2).
4. Определяем горизонтальные проекции точек: М1 Ù N 1 Ì f 1 ( А1 В1).
5. Определяем видимость проекций фронтали f ( AB ) по видимости проекций сферы Ф.
Решим задачу: Определить точки М и N пересечения прямой общего положения d ( AB ) со сферой Ф, (рис. 71).
Построение:
1. Способом замены плоскостей проекций преобразуем прямую a в линию уровня:
- на П4 линия сечения сферы плоскостью(а Ì S çç П4 ) спроецируется в окружность;
- в системе плоскостей П1/ П4 эта задача эквивалентна предыдущему примеру, рис.70.
2. Находим проекции точек:
d 4 Ç а4= М4, N 4 .
3. Обратным преобразованием определяем проекции точек М1 и N 1, а затем – М2 и N 2.
Рис. 71. Комплексный чертеж
ВОПРОСЫ ДЛЯ САМОПОДГОТОВКИ:
1. В чем заключается способ нахождения точек пересечения многогранной поверхности с прямой линией?
2. В чем заключается способ нахождения точек пересечения кривой поверхности с прямой линией?
3. В чем заключается общий прием построения точек пересечения прямой с поверхностью?
4. В каком случае при решении задач на построение точек пересечения прямой с поверхностью не используются проецирующие плоскости?
5. Как определить видимость проекций прямой?
ЛЕКЦИЯ № 7. ПОСТРОЕНИЕ ЛИНИИ ВЗАИМНОГО ПЕРЕСЕЧЕНИЯ КРИВЫХ ПОВЕРХНОСТЕЙ
Общие положения
Для построения линии взаимного пересечения двух кривых поверхностей пользуются методом вспомогательных секущих плоскостей.
В качестве этих поверхностей используются не только плоскости, но в некоторых случаях сферы и другие поверхности.
Вспомогательные поверхности выбирают таким образом, чтобы с данными поверхностями они пересекались по линиям, легко определяемыми на чертеже. Желательно, с этой точки зрения, чтобы эти линии получались прямыми или окружностями, что позволяет строить их только с помощью линейки и циркуля.
При изображении линии взаимного пересечения кривых поверхностей необходимо определять видимые и невидимые ее части, а также исследовать вопрос о видимости очерковых и других линий контуров данных поверхностей.
В общем случае, случае врезки, линия пересечения представляет собой плавную кривую, которая может распадаться на две части или более(случай проницания).
Порядок линии пересечения равен произведению порядков двух кривых поверхностей, участвующих в пересечении.
Точки опорные и промежуточные определяются при помощи способа вспомогательных поверхностей.
Дата: 2019-02-02, просмотров: 233.
