Прямая может принадлежать плоскости, пересекаться с ней и быть ей па­раллельной. Вопрос принадлежности прямой рассмотрен нами в п. 2.4.2. Рас­смотрим нахождение точки пересечения прямой с плоскостью.

Сначала определим точку пересечения прямой общего положения / с горизонтально - проецирующей плоскостью S, (рис. 34).

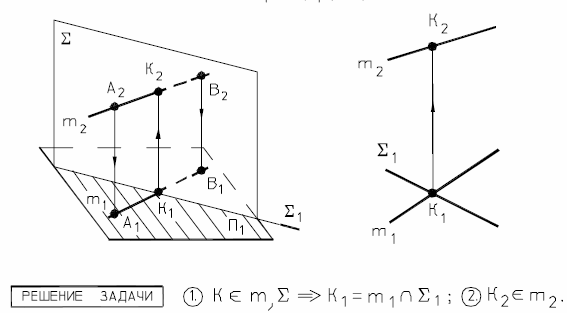
Рис. 34 - Пересечение прямой с горизонтально-проецирующей плоскостью

На этом же чертеже показано определение видимости участков прямой m, если считать плоскость Σ непрозрачной.

Определим теперь точку пересечения прямой общего положения q с плос­костью общего положения Г ( АВС), (рис. 35).

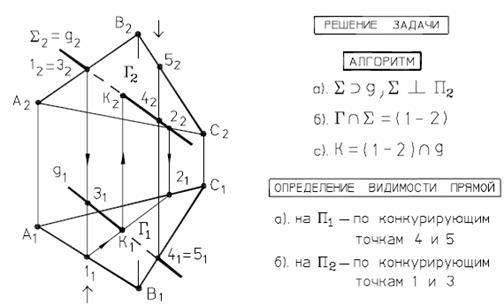
Рис. 35 - Пересечение прямой общего положения с плоскостью
общего положения

Эта задача решается с помощью вспомогательной проецирующей плоско­сти.

Проводим через q фронтально-проецирующую плоскость Σ ₂ = q ₂.

Находим проекции линии пересечения Σ и Г: 1₂2₂ - фронтальная проекция; 1₁2₁ - горизонтальная проекция; К=> q ∩ Г ( АВС).

Видимость участков прямой q определяем с помощью конкурирующих точек 1,3 и 4,5.

Прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в этой плоскости.

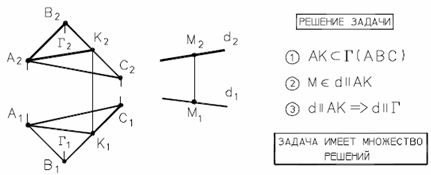
Рис. 36 - Параллельность прямой и плоскости

Если прямая перпендикулярна плоскости, то горизонтальная проекция этой прямой перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция – фронтальной проекции фронтали той же плоскости.

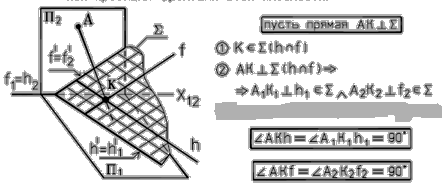
Рис. 37 - Прямая линия, перпендикулярная плоскости

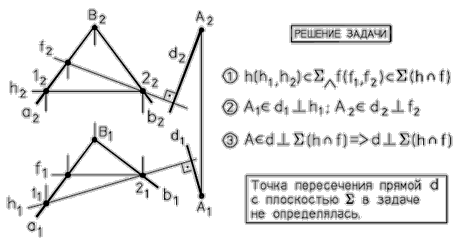
Рис. 38 - Перпендикулярность прямой к плоскости
на комплексном чертеже

Параллельные и взаимно перпендикулярные плоскости

     Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

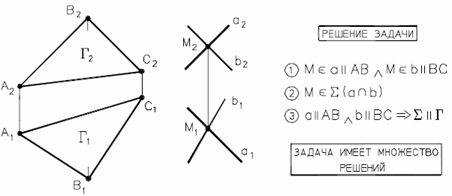
Рис. 39 - Взаимопараллельные плоскости

     Если плоскость проходит через перпендикуляр к другой плоскости, то она перпендикулярна этой плоскости.

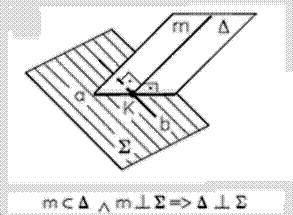
Рис. 40 - Перпендикулярность плоскостей в пространстве

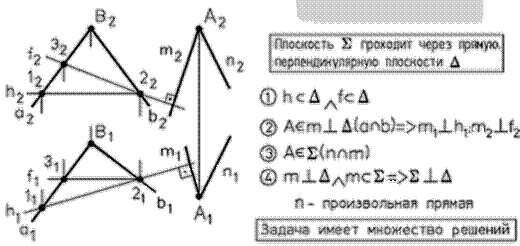
Рис. 41 - Перпендикулярность плоскостей на комплексном чертеже

ВОПРОСЫ ДЛЯ САМОПОДГОТОВКИ.

1. Какое положение в пространстве могу занимать две плоскости?

2. По какому алгоритму строится линия пересечения плоскостей общего положения?

3. Как строится линия пересечения плоскостей, заданных многоугольниками?

4. По какому алгоритму строится точка пересечения плоскости общего положения с прямой общего положения?

5. Какое условие параллельности прямой и плоскости?

6. Какое условие перпендикулярности прямой и плоскости?

7. Какое условие параллельности двух плоскостей?

8. Какое условие перпендикулярности двух плоскостей?

9. Как определяется видимость участков прямой при пересечении ее с плоскостью?

10. Как определяется взаимная видимость пересекающихся плоскостей?

ЛЕКЦИЯ № 4. СПОСОБЫ ПРЕОБРАЗОВАНИЯ
КОМПЛЕКСНОГО ЧЕРТЕЖА

Решение многих задач начертательной геометрии упрощается, если гео­метрические объекты занимают относительно плоскостей проекций некоторое частное положение. Например, если геометрический объект (прямая, плоская фигура) расположен в плоскости, параллельной плоскости проекций, то на эту плоскость он проецируется в натуральную величину, что позволяет очень просто решать метрические задачи, связанные с определением натуральных размеров геометрических объектов. А вот при определении расстояния от точки до плос­кости удобно, чтобы плоскость была проецирующей.

В связи с этим возникает следующая идея решения метрических и позици­онных задач начертательной геометрии: посредством изменения взаимного по­ложения геометрических объектов и плоскостей проекций добиться удобного для данного конкретного случая относительного положения.

Этого можно добиться двумя способами:

1) положение оригинала в пространстве остается неизменным, а заменяют одну или обе плоскости проекций (способ замены плоскостей проекций);

2) неизменной остается система плоскостей проекций, а меняют положение оригинала в пространстве (способы плоскопараллельного перемещения и
вращения).