Определение натуральной величины отрезка прямой и углов ее наклона к плоскостям проекций

На рис.15 представлено наглядное изображение отрезка АВ и его проек­ции на плоскости П₁ и П₂.

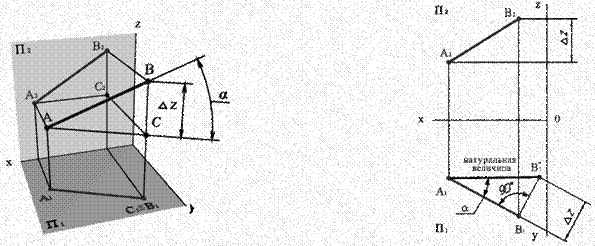
Рис. 15 - Наглядное изображение отрезка АВ прямой

Из геометрических соотношений на рис.15 понятно:

- Δ ΑΒС прямоугольный, причем ВС = В₂С₂ =∆z;

Отсюда вытекает следующее правило:

Натуральная величина отрезка прямой равна гипотенузе прямоуголь­ ного треугольника, у которого одним катетом является проекция отрезка на какую-либо из плоскостей проекций, а вторым катетом - разность рас­стояний концов отрезка от этой же плоскости проекций.

В отмеченном треугольнике α - угол наклона прямой к П₁ .

Используем сформулированное правило для решения задачи на комплекс­ном чертеже.

Определим натуральную величину отрезка АВ, а также α, β по заданным проекциям (рис. 16).

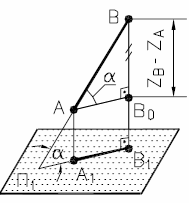а) в пространстве	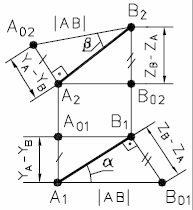б) в проекциях
Рис. 16 - Определение натуральной величины отрезка АВ способом прямоугольного треугольника

Проверка правильности построений: Α₁Β₀₁ = А₀₂В₂= 1АВ1.

Взаимное положение двух прямых в пространстве

Прямые в пространстве могут быть:

а) параллельные - 11;

б)пересекающиеся - ∩;

в) скрещивающиеся - ·_;

Если прямые параллельны, то их одноименные проекции параллельны (рис. 17).

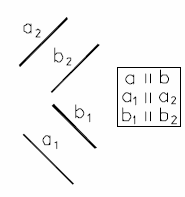
Рис. 17 - Параллельные прямые

Если прямые пересекаются, то точки пересечения их одноименных проек­ций лежат на линии проекционной связи, (рис. 18).

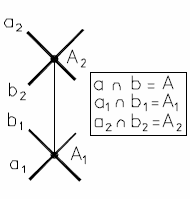
Рис. 18 - Пересекающиеся прямые

Точки пересечения одноименных проекций скрещивающихся прямых не лежат на общей линии проекционной связи, (рис. 19).

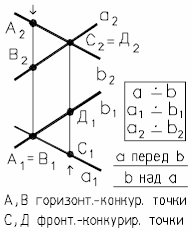
Рис. 19 - Скрещивающиеся прямые

Точки, лежащие на проецирующей прямой, называются конкурирующими. Конкурирующие точки удобно использовать при определении видимости эле­ментов фигур.

Из двух конкурирующих точек относительно П₁ видимой на П₁ является

та, высота которой больше.

Из двух конкурирующих точек относительно П₂ видимой на П₂ является та, глубина которой больше.

Из анализа проекций конкурирующих точек A, B и C, D, (рис. 19), можно сде­лать вывод, что прямая a проходит перед b и b над прямой a.

Проецирование прямого угла

Общее положение:

Если две стороны любого угла параллельны плоскости проекций, то он проецируется на эту плоскость в натуральную величину.

Для прямого угла достаточно параллельности лишь одной стороны, то есть:

Если одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то он проецируется на эту плоскость в на­ туральную величину, то есть в виде прямого угла, (рис. 20).

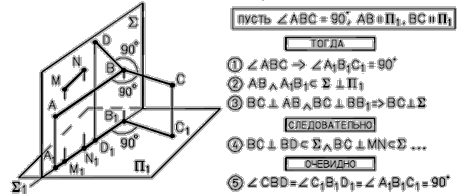Рис. 20 - Проецирование прямого угла