Таким образом, задача сводится к определению расстояния от точки до плоскости и может быть решена теми же способами.
Рассмотрим примеры:
Задача 1. Определить расстояние между скрещивающимися прямыми a и b.
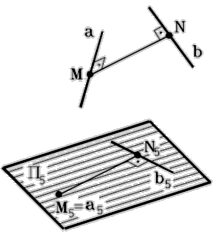Рис. 87 - Пространственная модель
| Схема решения: 1. Расстояние между скрещивающимися прямыми a и b определяется длиной отрезка MN одновременно перпендикулярного к обоим прямым, (рис. 87). 2. На плоскость, перпендикулярную к одной из прямых, отрезок MN проецируется в истинную величину. |
Алгоритм:
1. Преобразовать прямую a или b в проецирующую, например, способом замены плоскостей проекций.
2. Построить проекцию M 5 N 5 отрезка MN на плоскость П5 ^ a . M 5 N 5 – искомое расстояние.
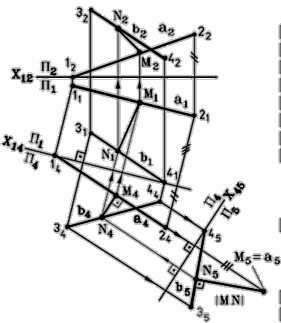Рис. 88 - Комплексный чертеж
| Построение, (рис. 88): 1. Проводим ось проекций Х12. 2. Новая ось проекций Х14 çç a 1. 3. Строим проекцию прямой a на П4. 4. Строим проекцию прямой b на П4. 5. Новая ось проекций Х45 ^ a 4 . 6. Строим проекцию прямой b на П5. 7. Строим проекцию прямой a на П5. 8. M 5 N 5 = ç MN ç- искомый отрезок, т.к. в системе плоскостей П4/ П5 MN – линия уровня, поэтому M 5 N 5 Ç b 5 = 90 °. 9. Строим проекцию отрезка MN на П4, т.к. в системе плоскостей П4/ П5 MN – линия уровня, поэтому M 4 N 4 çç Х45. 10. Строим проекцию отрезка MN на П1 . 11. Строим проекцию отрезка MN на П2 |
Задача 2. Определить расстояние от точки А до поверхности конуса Ф, (рис. 89).
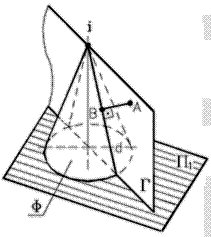Рис. 89 - Пространственная модель
| Схема решения: 1. Расстояние от точки А до поверхности вращения Ф, (независимо от ее вида), определяется длиной перпендикуляра АВ, опущенного из точки А на ближайшую к ней образующую (меридиан) поверхности d. 2. Образующая d принадлежит плоскости Г, проходящей через данную точку А и ось вращения i поверхности Ф. |
Алгоритм:
1. Через точку А и ось i проводим плоскость Г.
2. Находим образующую d ( d = Г Ç Ф).
3. Преобразуем образ d в прямую уровня способом замены плоскостей проекций.
4. В новой системе плоскостей из точки А опускаем перпендикуляр АВ на образ d.
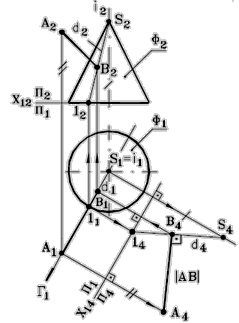Рис. 90 - Комплексный чертеж
| Построение, (рис. 90): 1. Плоскость Г(А, i); Г ^ П1 . 2. Образующая d (1 – S )= Г Ç Ф. 3. Проводим ось Х12. 4. Новая ось проекций Х14 çç Г1. 5. Строим проекцию образующей d на П4, в системе плоскостей П1/ П4 d ( d 4 ) – линия уровня (фронталь). 6. А4В4 ^ d 4, в системе плоскостей П1/ П4, А4В4 = ç АВ ç- искомый отрезок. 7. Строим проекцию отрезка АВ на П1 . 8. Строим проекцию отрезка АВ на П2. |
8.4. Задачи на определение действительных величин углов
между геометрическими фигурами
Угол между двумя пересекающимися прямыми проецируется без искажения на плоскости, параллельной плоскости угла.
Угол между двумя скрещивающимися прямыми линиями измеряется углом между двумя пересекающимися прямыми, параллельными данным скрещивающимся прямым.
Рассмотрим примеры: Задача 1. Определить угол a между прямой d и плоскостью D ( m çç n ).
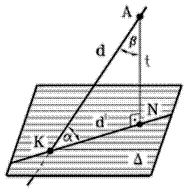Рис. 91 - Пространственная модель
| Угол наклона прямой d к плоскости D измеряется величиной линейного угла a между прямой d и ее прямоугольной проекцией d ¢ на данную плоскость D, (рис. 91). |
Схема решения:
1. Из произвольной точки А Î d опускаем перпендикуляр t на плоскость D.
2. Определяем точку N встречи перпендикуляра t с плоскостью D.
3. Определяем точку К пересечения прямой d с плоскостью D.
4. Строим прямоугольную проекцию d ¢ (К N ) прямой d (АК) на плоскость D.
5. Угол AKN – искомый.
Решение задачи значительно упрощается, если вместо угла a определять дополнительный до 90º угол b. В этом случае не требуется находить точку N и проекцию прямой d ¢. Зная величину угла b, вычисляем угол a: a =90 ° - b.
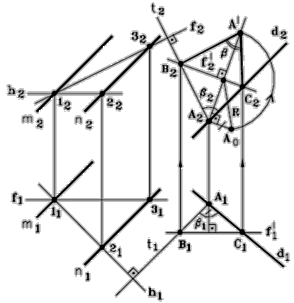 Рис. 92 - Комплексный чертеж
| Построение, (рис. 92): 1. h Î D ( m çç n ), f Î D ( m çç n ). 2. Выбираем произвольную точку А Î d. 3. А Î t ^ D. 4. S = d Ç t. 5. Строим отрезок ВС = f ¢¢ Î S. 6. Ð ВАС = d ^t= b Î S. 7. Определяем величину угла b способом вращения его вокруг f ¢до положения çç П2. 8. Ð В2А ¢ С2 = ç b ç. 9. Искомый Ð a = 90 ° - b. |
Задача 2. Определить величину угла между плоскостями Г(а çç b ) и D ( c Ç d ), (рис. 93).
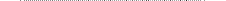Схема решения:
1. Угол между плоскостями Г и D измеряется одним из линейных углов, обычно острым, полученным при пересечении этих плоскостей третьей ( S ), перпендикулярной к ним.
2. В общем случае удобно определять угол b, заключенный между перпендикулярами опущенными из произвольной точки N на заданные плоскости Г и D.
3. Найденный угол b является искомым, если он
Рис.93 - Пространственная острый; если угол b - тупой, то искомый угол
модель a = 180º - b.
Агоритм:
1. Из точки N проводим прямые n ^ Г и m ^ D.
2. Определяем величину угла b, преобразовав плоскость S ( m Ç n ) способом вращения в плоскость уровня.
Рис. 94 - Комплексный чертеж
| Построение, (рис. 94): 1. h Ù f Î Г( a çç b/ 2. h ¢ Ù f ¢ Î D ( c Ç d )/ 3. Берем произвольную точку N. 4. N Î n ^ Г. 5. N Î m ^ D. 6. m Ç n = S. 7. Отрезок AB = f ¢¢ Î S. 8. Ð ANB = n ^ m = b Î S. 9. Способом вращения вокруг f ¢¢ преобразуем плоскость S ( D ANB ) в плоскость уровня S ¢ çç П2. 10. Треугольник A 2 N ¢ B 2 = ç ANB ç Þ Ð A 2 N ¢ B 2 – искомый. |
Задача 3. Определить величину двугранного угла между плоскостями Г и D, (рис. 95).
Схема решения:
1. Угол между плоскостями Г и D измеряется линейным углом, обычно острым, полученным при пересечении этих плоскостей третьей плоскостью ( S ), перпендикулярной к ним.
2. Т.к. линия пересечения плоскостей Г и D известна – ребро MN, то решение задачи упрощается – угол спроецируется в конгруэнтный ему на плоскость, перпендикулярную ребру MN.
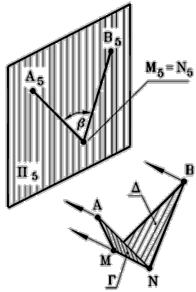Рис. 95 - Пространственная модель
| Алгоритм: 1. Преобразуем ребро MN способом замены плоскостей проекций в прямую уровня M 4 N 4. 2. Преобразуем ребро M 4 N 4 способом замены плоскостей проекций в проецирующую прямую M 5 N 5. Построение, (рис. 96): 1. Проводим ось проекций Х12. 2. Проводим ось проекций Х14 ççM 1 N 1 . 3. Строим проекцию ребра MN на П4, в системе плоскостей П1/ П4 4. MN ( M 4 N 4 ) – линия уровня. 5. Строим проекцию плоскости Г(Г4) на П4. 6. Строим проекцию плоскости D ( D 4 ) на П4. 7. Проводим ось проекций Х45 ^ M 4 N 4 . 8. Строим проекцию ребра MN на П5, в системе плоскостей П4/ П5 MN ( M 5 N 5 ) – проецирующая прямая. 9. Строим проекцию плоскости Г(Г5) на П5. 10. Строим проекцию плоскости D ( D 5 ) на П5. 11. Плоскости Г и D ^ П5 Þ ÐA 5 M 5 B 5 – искомый.
|
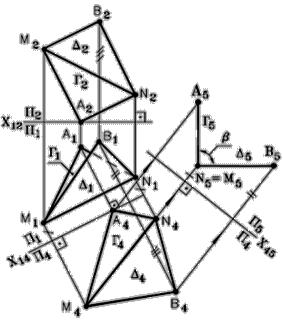Рис. 96 - Комплексный чертеж
|
8.5. Задачи на определение действительных величин
плоских геометрических фигур
Построение плоской фигуры, обладающей определенными метрическими свойствами, требует изображения на чертеже ее натурального вида.
Рассмотрим пример: Задача 1. Определить действительную величину треугольника АВС, (рис.97).
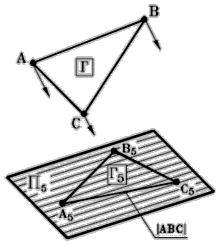Рис. 97 - Пространственная модель
| Схема решения: Преобразовать заданную плоскую фигуру Г( D АВС) в плоскость уровня. Алгоритм: Если Г является плоскостью общего положения, то необходимо: 1. Преобразовать плоскость общего положения Г( D АВС) в проецирующую плоскость (Г4), например способом замены плоскостей проекций. 2. Преобразовать, полученную проецирующую плоскость (Г4), в плоскость уровня (Г5), например, способом замены плоскостей проекций. |
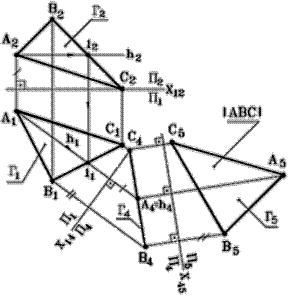Рис. 98 - Комплексный чертеж
| Построение, (рис. 98): 1. Строим горизонталь плоскости h. 2. Проводим ось проекций Х12. 3. Проводим новую ось проекций Х14 ^ h 1. 4. Строим проекцию Г( D АВС) на П4, Г(Г1, Г4) – проецирующая плоскость. 5. Проводим новую ось проекций Х45 çç Г4. 6. Строим проекцию Г( D АВС) на П5, Г(Г4, Г5) – плоскость уровня. 7. Г5 ( D А5В5С5) = ç ( D АВС ç- действительная (натуральная) величина плоскости Г( D АВС) . |
8.6. Задачи на построение в плоскости общего положения
геометрических фигур по заданным размерам
Рассмотрим пример: Задача 1. В плоскости Г(а Ç b ) построить равносторонний треугольник АВС, вписанный в окружность радиуса R, (рис. 99).
Схема решения:
1. Преобразуем плоскость Г в плоскость уровня Г5 двукратной заменой плоскостей проекций.
2. Треугольник АВС Î Г5 .
3. Обратными преобразованиями строим А1В1С1 и А2В2С2.
Построение:
1. Строим горизонталь плоскости h.
2. Проводим ось проекций Х12.
3. Проводим новую ось проекций Х14 ^ h 1.
4. Строим проецирующую плоскость Г4.
5. Проводим новую ось проекций Х45 çç Г4.
6. Строим плоскость уровня Г5.
7. Строим окружность ç R ï Î Г.
8. Строим треугольник А5В5С5 Î Г5.
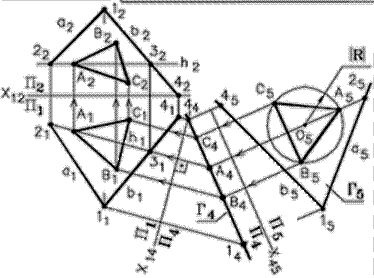
Рис. 99 - Комплексный чертеж
9. Обратным преобразованием строим горизонтальную проекцию треугольника АВС на плоскости П1, D А1В1С1.
10. Затем строим на плоскости П2, фронтальную проекцию треугольника АВС, D А2В2С2.
ВОПРОСЫ ДЛЯ САМОПОДГОТОВКИ:
1. Какие задачи называются метрическими?
2. На какие основные группы делятся метрические задачи?
3. Какое из свойств ортогонального проецирования является теоретической основой для решения метрических задач?
4. Какие способы преобразования комплексного чертежа используют при решении метрических задач?
5. Какова общая схема решения задач на определение расстояний между геометрическими фигурами?
6. Какова общая схема решения задач на определение действительных величин углов между геометрическими фигурами?
7. Какова общая схема решения задач на определение действительных величин плоских геометрических фигур?
8. Какова общая схема решения задач на построение в плоскости общего положения геометрических фигур по заданным размерам?
Дата: 2019-02-02, просмотров: 293.
