По курсу
Начертательная геометрия
(для студентов заочной формы обучения
всех специальностей академии )
Харьков – ХНАГХ - 2007
Конспект лекций по курсу начертательная геометрия (для студентов заочной формы обучения всех специальностей академии). Сост. Лусь В.И.
– Харьков: ХНАГХ, 2007. – 79 с.
Составитель: В.И. Лусь
Рекомендовано кафедрой инженерной и компьютерной графики, протокол № 7 от 28 февраля 2007 г.
 |
ВВЕДЕНИЕ
В число дисциплин, составляющих основу инженерного образования, входит начертательная геометрия.
Предметом начертательной геометрии является изложение и обоснование способов построения изображений пространственных форм на плоскости.
Изображения, построенные по правилам, изучаемым в начертательной геометрии, позволяют представить мысленно форму предметов и их взаимное расположение в пространстве, определить их размеры, исследовать геометрические свойства, присущие изображаемому предмету.
Начертательная геометрия развивает пространственное воображение и передает ряд своих выводов в практику выполнения чертежей, обеспечивая их выразительность и точность, а, следовательно – и возможность изготовления по этим чертежам изделий. Овладение чертежом как средством выражения технической мысли и как производственным документом происходит на протяжении всего процесса обучения в ВУЗе при изучении общеинженерных и специальных дисциплин, а также при выполнении курсовых и дипломных проектов.
В курсе лекций рассмотрение метода проекций начинается с построения проекций точки, так как при построении изображения любой пространственной формы рассматривается ряд точек, принадлежащих этой форме.
Сегодня одним из направлений перестройки высшей школы является усиление самостоятельности, предоставляемой студентам при изучении той или иной дисциплины. Правильно построенные самостоятельные занятия по начертательной геометрии разрешат трудности в изучении этой дисциплины.
Для повторения и закрепления изучаемого материала, в целях самопроверки, к материалу каждой лекции имеется значительное число вопросов, на которые необходимо ответить.
Указана учебная литература, для желающих ознакомиться с различными вариантами изложения разделов программы и с некоторыми дополнительными вопросами начертательной геометрии.
ЛЕКЦИЯ № 1. СПОСОБЫ ПРОЕЦИРОВАНИЯ. ТОЧКА И ПРЯМАЯ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ
Прямая на комплексном чертеже
Прямые частного положения
Прямая, параллельная одной плоскости проекций, называется прямой уровня.
Прямая, параллельная плоскости П1 называется горизонтальной прямой и обозначается h.
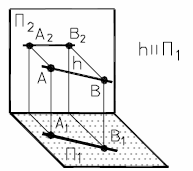
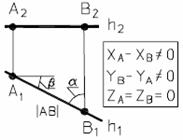
На рис. 10а и 10б представлены наглядный и комплексный чертеж горизонтальной прямой.
| 
|
| а) наглядный чертеж прямой | б) комплексный чертеж прямой |
| Рис. 10 - Горизонтальная прямая | |
Основное свойство горизонтальной прямой: h 211 оси X12.
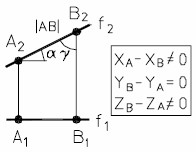
Прямая, параллельная плоскости П2, называется фронтальной прямой и обозначается f.
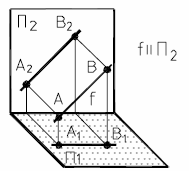
На рис. 11а и 11б представлены наглядный и комплексный чертеж фронтальной прямой.
 а)
а)
|  б)
б)
|
| Рис. 11 - Фронтальная прямая | |
Основное свойство фронтальной прямой: f1 II оси X12.
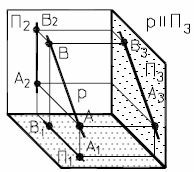
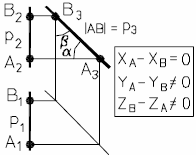
Прямая, параллельная плоскости П3, называется профильной прямой и обозначается р.
На рис. 12а и 12б представлены наглядный и комплексный чертеж профильной прямой.
 а)
а)
|  б)
б)
|
| Рис. 12 - Профильная прямая | |
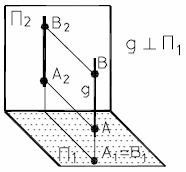
Прямая, параллельная двум плоскостям проекций (перпендикулярная третьей), называется проецирующей прямой.
На рис.13а и 13б представлены наглядный и комплексный чертеж горизонтально-проецирующей прямой.
 а)
а)
| 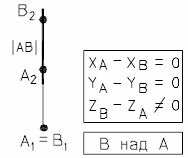 б)
б)
|
| Рис. 13 - Горизонтально-проецирующая прямая | |
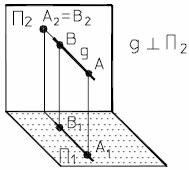
На рис.14а и 14б представлены наглядный и комплексный чертеж фронтально-проецирующей прямой.
 | 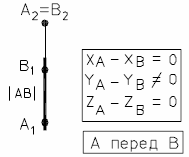 | ||
а) б)
Рис. 14 - Фронтально-проецирующая прямая
ВОПРОСЫ ДЛЯ САМОПОДГОТОВКИ:
1. Что называется проекцией, проецированием и каковы основные виды проецирования?
2. В чем заключается метод построения комплексного чертежа точки?
3. Каковы законы построения третьей проекции точки по двум заданным ее проекциям?
4. Определяет ли одна проекция точки ее положение в пространстве?
5. Как определить высоту и глубину точки по ее комплексному чертежу?
6. Какие точки называются конкурирующими?
7. Как определить видимость точек по комплексному чертежу?
8. Какие Вы знаете инварианты ортогонального проецирования?
9. Как располагаются на комплексном чертеже проекции прямой общего положения?
10. Какое положение по отношению к плоскостям проекций может занимать прямая? Какие прямые частного положения Вы знаете?
Проецирование прямого угла
Общее положение:
Прямая и точка в плоскости
Два признака принадлежности прямой плоскости:
1. Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие данной плоскости, (рис. 26).
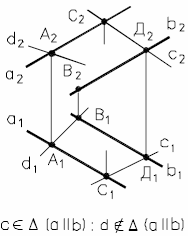
Рис. 26
2. Точка принадлежит плоскости, если она лежит на прямой, принадлежащей плоскости, (рис. 27).
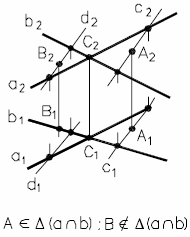
Рис. 27 - Принадлежность точки плоскости
Линии уровня плоскости
Горизонтали – прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций П1. Фронтальная проекция горизонтали как линии, параллельной плоскости П1, - горизонтальна.
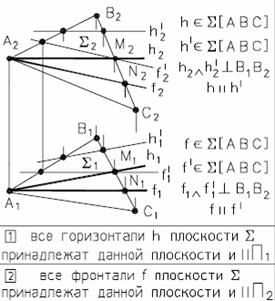
Рис. 28 - Линии уровня в плоскости
Фронтали – прямые, расположенные в плоскости и параллельные плоскости проекций П2, (рис. 28). Горизонтальная проекция фронтали как линии, параллельной плоскости П2, - горизонтальна.
Если прямая перпендикулярна плоскости, то горизонтальная проекция этой прямой перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция – фронтальной проекции фронтали той же плоскости.
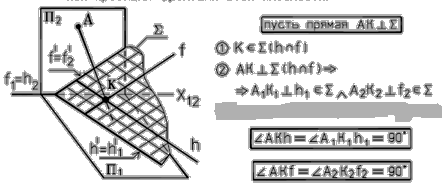
Рис. 37 - Прямая линия, перпендикулярная плоскости
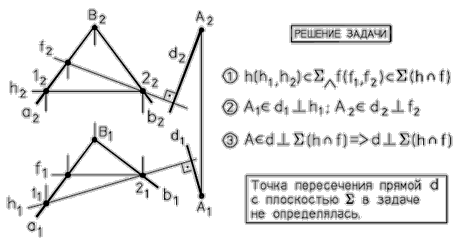
Рис. 38 - Перпендикулярность прямой к плоскости
на комплексном чертеже
ВОПРОСЫ ДЛЯ САМОПОДГОТОВКИ.
1. Какое положение в пространстве могу занимать две плоскости?
2. По какому алгоритму строится линия пересечения плоскостей общего положения?
3. Как строится линия пересечения плоскостей, заданных многоугольниками?
4. По какому алгоритму строится точка пересечения плоскости общего положения с прямой общего положения?
5. Какое условие параллельности прямой и плоскости?
6. Какое условие перпендикулярности прямой и плоскости?
7. Какое условие параллельности двух плоскостей?
8. Какое условие перпендикулярности двух плоскостей?
9. Как определяется видимость участков прямой при пересечении ее с плоскостью?
10. Как определяется взаимная видимость пересекающихся плоскостей?
ЛЕКЦИЯ № 4. СПОСОБЫ ПРЕОБРАЗОВАНИЯ
КОМПЛЕКСНОГО ЧЕРТЕЖА
Решение многих задач начертательной геометрии упрощается, если геометрические объекты занимают относительно плоскостей проекций некоторое частное положение. Например, если геометрический объект (прямая, плоская фигура) расположен в плоскости, параллельной плоскости проекций, то на эту плоскость он проецируется в натуральную величину, что позволяет очень просто решать метрические задачи, связанные с определением натуральных размеров геометрических объектов. А вот при определении расстояния от точки до плоскости удобно, чтобы плоскость была проецирующей.
В связи с этим возникает следующая идея решения метрических и позиционных задач начертательной геометрии: посредством изменения взаимного положения геометрических объектов и плоскостей проекций добиться удобного для данного конкретного случая относительного положения.
Этого можно добиться двумя способами:
1) положение оригинала в пространстве остается неизменным, а заменяют одну или обе плоскости проекций (способ замены плоскостей проекций);
2) неизменной остается система плоскостей проекций, а меняют положение оригинала в пространстве (способы плоскопараллельного перемещения и
вращения).
Сечение цилиндра плоскостью
При пересечении цилиндра вращения с плоскостью могут быть получены: окружность (Г ^ i), эллипс (Δ∩i под Ða), две параллельные прямые (S11i).
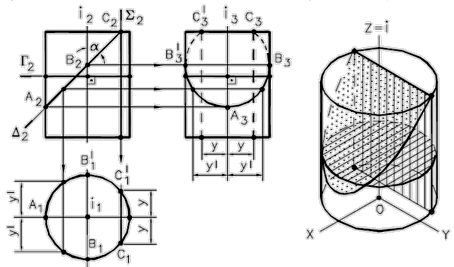
Рис. 58 - Пересечение цилиндра плоскостью
При пересечении конуса вращения с плоскостью могут быть получены все кривые 2-го порядка: окружность, эллипс, парабола, гипербола, а в случае прохождения секущей плоскости через вершину – точка, прямая, две прямые образующие.
Сечение конуса плоскостью
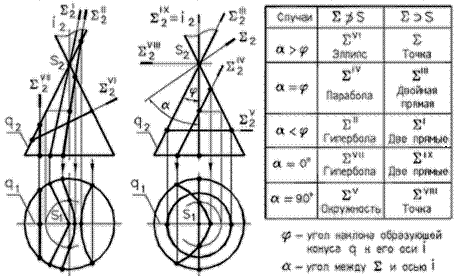
Рис. 59 - Пересечение конуса плоскостью
Сечение сферы плоскостью
Любая плоскость всегда пересекает сферу по окружности.
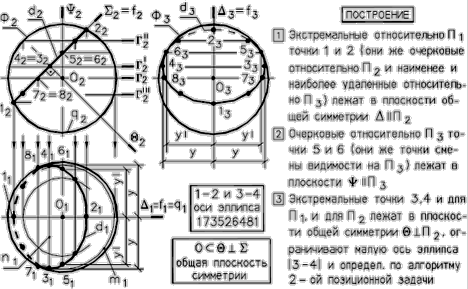
Рис. 60 - Пересечение сферы плоскостью
Сечение тора плоскостью
В общем случае тор пересекается с плоскостью по кривой 4-го порядка.
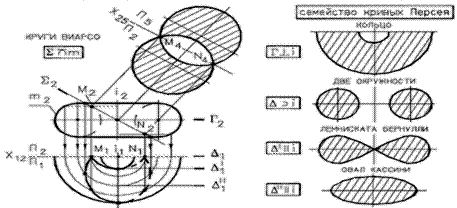 |
Рис. 61 - Пересечение тора плоскостью
ВОПРОСЫ ДЛЯ САМОПОДГОТОВКИ:
1. Что называется многогранником?
2. Условие принадлежности точки многограннику?
3. Из каких элементов состоит гранная поверхность?
4. Приведите примеры кривых поверхностей.
5. Как образуется цилиндрическая поверхность?
6. Как образуется коническая поверхность?
7. Как образуется сферическая поверхность?
8. Что такое поверхность вращения?
9. Назовите цилиндрические сечения.
10. Назовите конические сечения.
Общие положения
1. Число точек пересечения соответствует порядку заданной поверхности Ф.
2. В основу построения положен способ вспомогательных поверхностей
3. В качестве вспомогательных поверхностей обычно выбирают плоскости S , проходящие через заданную прямую n.
4. Плоскость S должна пересекать Ф по линии d, проекции которой были бы графически простыми (дуга окружности или прямая).
5. Видимость проекций прямой n по видимости проекций поверхности.
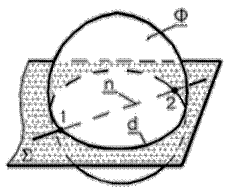 Рис. 62 - Пересечение прямой с поверхностью
Рис. 62 - Пересечение прямой с поверхностью
| Алгоритм построения: - S É n ; - S Ç F = d ; - 1, 2 = d Ç n. |
6.2. Построение точек пересечения прямой с
поверхностью многогранника
Поверхность многогранника представляет собой совокупность пересекающихся плоскостей. Поэтому решение данной задачи, по существу, является двукратным определением точки пересечения прямой линии с плоскостью (см. раздел 3.2, рис.35).
Схема решения выглядит так:
- плоскость S, проходящая через прямую n, пересечет многогранник по плоской замкнутой ломаной линии 1-2-3-1;
- искомые точки M и N есть результат пересечения линии 1-2-3-1 с прямой n.
Алгоритм решения задачи:
1. S É n , S - проецирующая плоскость.
2. S Ç F = ( 1-2-3-1).
3. М =(1-2-3-1) Ç n = F Ç n ,
N = ( 1-2-3-1) Ç n = F Ç n .
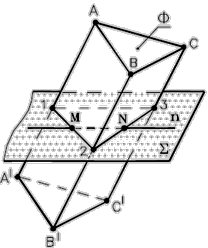 Рис.63 - Определение точек пересечения прямой с поверхностью многогранника (пространственный пример)
Рис.63 - Определение точек пересечения прямой с поверхностью многогранника (пространственный пример)
| Рассмотрим пример: Определить точки М и N пересечения прямой общего положения n с поверхностью Ф пирамиды SABC. Построение: 1. Через прямую n проводим горизонтально проецирующую плоскость S . 2. Определяем горизонтальную проекцию ломаной: S 1 Ç Ф1 = (11 – 21 – 31- 11). 3. Определяем фронтальные проекции вершин ломаной: 12 Ì А2 В2, 22 Ì S 2 B 2 , 32 Ì B 2 C 2 . 4. Строим фронтальную проекцию ломаной: 12 – 22 – 32- 12. 5. Определяем фронтальные проекции искомых точек: (12 – 22 – 32- 12) Ç n 2 = М2 Ù N 2 . 6. Определяем горизонтальные проекции точек: М1 Ì n 1 Ù N 1 Ì n 1 . 7. Определяем видимость проекций прямой n по dидимости проекций граней пирамиды. |
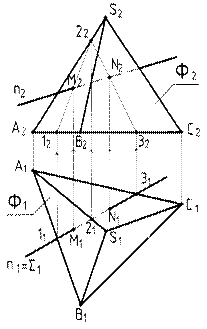 Рис.64 - Определение точек пересечения прямой n с поверхностью пирамиды
Рис.64 - Определение точек пересечения прямой n с поверхностью пирамиды
|
6.3. Построение точек пересечения прямой
с поверхностью цилиндра
На рис. 65 и 66 построены точки пересечения поверхности эллиптического цилиндра a с прямой линией m .
Через прямую m проведена плоскость w , пересекающая цилиндрическую поверхность по образующим. Для этого, как известно, плоскость должна быть параллельна образующим (или оси) цилиндра. На рисунках она определена прямой m и прямой а, проходящей через некоторую точку А прямой m и параллельно оси цилиндра:
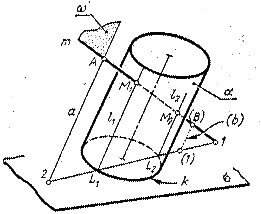 Рис. 65 - Пространственная модель
Рис. 65 - Пространственная модель
|
w = ( m Ç a = А ). Другие плоскости, в частности проецирующие, проходящие через прямую m , дадут в сечении цилиндра более сложные кривые линии.
Для построения линии пересечения плоскости w и цилиндрической поверхности, т.е. двух образующих цилиндра, должна быть проведена вспомогательная секущая плоскость. В качестве нее выбрана плоскость s основания цилиндра, что позволяет не строить линию пересечения этой плоскости с цилиндрической поверхностью, так как она уже начерчена – это кривая линия основания k. Плоскость s пересекается с плоскостью w по прямой 1 – 2. На рис. 66 эта линия очевидна, так как плоскость s - проецирующая. В случае, если прямая m пересекается с плоскостью s за пределами чертежа, точку (1) находят с помощью какой-либо дополнительной прямой, например (b ), взятой в плоскости w, (рис. 65). Точки L 1 и L 2 пересечения линий k и (1 – 2) принадлежат образующим l 1 и l 2 сечения цилиндра плоскостью w: w Ç a = ( l 1 , l 2 ). |
 Рис. 66 - Комплексный чертеж
Рис. 66 - Комплексный чертеж
|
Точки М1 и М2 пересечения этих образующих с прямой m являются искомыми:
М1 = l 1 Ç m, М2 = l 2 Ç m .
Отрезок М1 - М2 прямой линии m находится внутри цилиндра и изображен поэтому линией невидимого контура. На рис. 65 слева от точки М1 прямая m видна, так как эта точка лежит на видимой стороне поверхности цилиндра. Часть линии m справа от точки М2 остается невидимой, так как точка М2 лежит на невидимой стороне поверхности a . Аналогично решается вопрос видимости на каждой проекции, рис. 66. Для уточнения видимости плохо различимого участка прямой m элемент I этого чертежа показан в более крупном масштабе.
Общие положения
Для построения линии взаимного пересечения двух кривых поверхностей пользуются методом вспомогательных секущих плоскостей.
В качестве этих поверхностей используются не только плоскости, но в некоторых случаях сферы и другие поверхности.
Вспомогательные поверхности выбирают таким образом, чтобы с данными поверхностями они пересекались по линиям, легко определяемыми на чертеже. Желательно, с этой точки зрения, чтобы эти линии получались прямыми или окружностями, что позволяет строить их только с помощью линейки и циркуля.
При изображении линии взаимного пересечения кривых поверхностей необходимо определять видимые и невидимые ее части, а также исследовать вопрос о видимости очерковых и других линий контуров данных поверхностей.
В общем случае, случае врезки, линия пересечения представляет собой плавную кривую, которая может распадаться на две части или более(случай проницания).
Порядок линии пересечения равен произведению порядков двух кривых поверхностей, участвующих в пересечении.
Точки опорные и промежуточные определяются при помощи способа вспомогательных поверхностей.
Примеры соосных поверхностей вращения
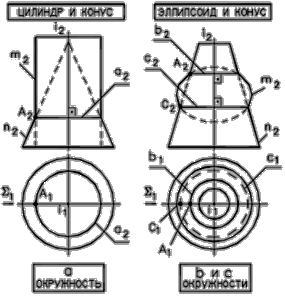 Рис. 76 - Примеры пересечения Рис. 76 - Примеры пересечения
| 1. Меридианы m и n поверхностей, расположенные в одной осевой плоскости (S ), пересекаются в некоторых точках А и С. 2. Точки пересечения меридианов при их вращении описывают окружности, принадлежащие обеим поверхностям и являющиеся линиями их пересечения. 3. Число окружностей при пересечении поверхностей равно числу точек пересечения их меридианов m и n, расположенных по одну сторону от оси вращения i. соосных поверхностей вращения |
7.3.2. Примеры соосных поверхностей вращения,
одна из которых сфера
Особое место при пересечении соосных поверхностей вращения отводится сферам, свойства которых используются в дальнейшем при построении линии пересечения кривых поверхностей.
1.  Сфера имеет бесчисленное множество осей вращения
Сфера имеет бесчисленное множество осей вращения
2. Все оси вращения сферы проходят через ее центр
3. Если одной из двух соосных поверхностей вращения является сфера, то ее центр располагается на оси другой поверхности.
Рис. 77 - Примеры пересечения
соосных поверхностей вращения,
одна из которых сфера
7.3.3. Пересечение соосных поверхностей вращения
в элементах конструкций
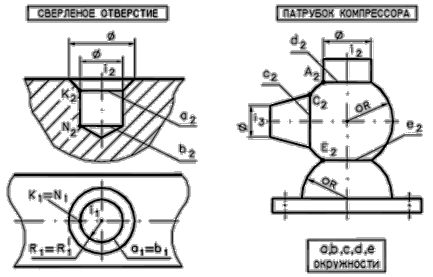
Рис. 78 - Пересечение соосных поверхностей вращения в элементах конструкций
СПОСОБ ВСПОМОГАТЕЛЬНЫХ СФЕР
Для построения линии пересечения поверхностей вращения, имеющих круговые сечения, в ряде случаев в качестве вспомогательных поверхностей целесообразно использовать сферы.
Разновидности способа включают в себя: способ концентрических сфер и способ эксцентрических сфер.
Способ концентрических сфер применяется, если:
- оси поверхностей пересекаются;
- есть общая плоскость симметрии;
- если способ вспомогательных секущих плоскостей не дает простого решения.
Способ эксцентрических сфер применяется, если:
- оси поверхностей скрещиваются;
- есть общая плоскость симметрии;
- каждая из поверхностей имеет семейство круговых сечений;
- если способ вспомогательных секущих плоскостей не дает простого решения.
В данном курсе лекций мы рассмотрим только способ концентрических сфер.
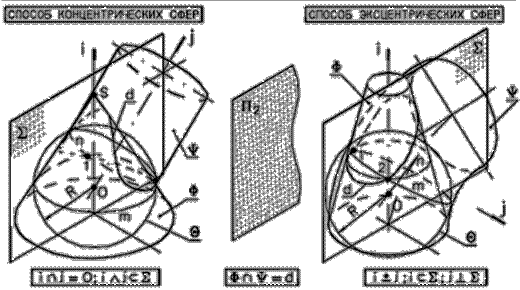
Рис. 79 - Пространственная иллюстрация способа вспомогательных сфер
СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР
Обоснование способа заключается в свойстве сферы пересекаться по окружностям с соосными с ней поверхностями вращения.
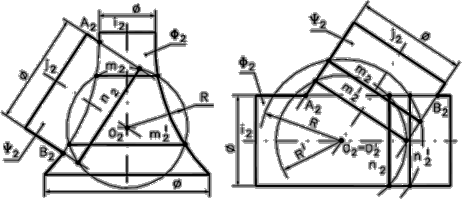
Рис. 80 - Обоснование способа концентрических сфер
Геометрическим местом центров (О, О¢, …) сфер (R, R¢, ….), дающих круговые сечения (m, m¢, …, n, n¢, …) одновременно с каждой из пересекающихся поверхностей вращения (Ф, Y, …), является точка пересечения их осей (i, j, …), рис.80.
Общие положения
Метрическими называются задачи, решение которых связано с определением характеристик геометрических фигур, определяемых (измеряемых) линейными и угловыми величинами.
Три основные группы задач:
1. Задачи на определение расстояний между геометрическими фигурами:
- расстояние между двумя точками;
- расстояние от точки до прямой общего положения;
- расстояние между параллельными прямыми;
- расстояние между параллельными плоскостями;
- расстояние между скрещивающимися прямыми (кратчайшее);
- расстояние от точки до плоскости;
- расстояние от точки до поверхности.
2. Задачи на определение углов между плоскими геометрическими фигурами:
- угол между пересекающимися и скрещивающимися прямыми;
- угол между прямой и плоскостью;
- угол между двумя плоскостями.
3. Задачи на определение действительных величин плоских геометрических фигур:
- действительная величина плоской фигуры.
ВОПРОСЫ ДЛЯ САМОПОДГОТОВКИ:
1. Какие задачи называются метрическими?
2. На какие основные группы делятся метрические задачи?
3. Какое из свойств ортогонального проецирования является теоретической основой для решения метрических задач?
4. Какие способы преобразования комплексного чертежа используют при решении метрических задач?
5. Какова общая схема решения задач на определение расстояний между геометрическими фигурами?
6. Какова общая схема решения задач на определение действительных величин углов между геометрическими фигурами?
7. Какова общая схема решения задач на определение действительных величин плоских геометрических фигур?
8. Какова общая схема решения задач на построение в плоскости общего положения геометрических фигур по заданным размерам?
Общие положения
При построении чертежа предмета, его обычно располагают так, чтобы направление трех главных измерений были параллельны плоскостям проекций, (рис. 100).
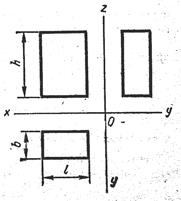
Рис. 100 - Трехпроекционный чертеж предмета
Направление длины – параллельно оси Х, ширины – оси У, высоты – оси Z. Тогда длина и высота проецируются в натуральную величину на фронтальную плоскость проекций, длина и ширина не искажаются на горизонтальной проекции, а ширина и высота – на профильной. Такой чертеж нетрудно строить, по нему просто производить измерения, судить о размерах изображенного предмета. Однако он недостаточно нагляден. На каждой из проекций отсутствует одно из трех измерений. Чтобы воспроизвести форму предмета, надо мысленно воссоздать ее по двум, трем, а иногда и большему числу проекций.
Более наглядный чертеж можно получить, проецируя предмет на одну плоскость проекций и располагая его так, чтобы ни одно из направлений главных измерений не проецировалось точкой.
На рис.101 изображен такой же параллелепипед, как и на рис.102, однако длина, ширина и высота его воспринимаются по одной проекции, так как взгляд «охватывает» сразу три стороны предмета.
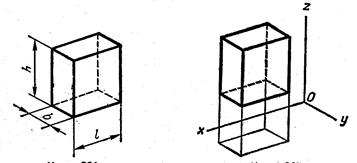
Рис. 101 Рис. 102
По такому чертежу легко представить себе его форму. Но он обладает двумя существенными недостатками: во-первых он необратим, так как представлена только одна проекция предмета; во-вторых, по такому чертежу нельзя произвести измерения предмета.
Чтобы ликвидировать первый недостаток, чертеж дополняют второй проекцией, называемой вторичной. Чтобы чертеж стал измеримым, на нем строят изображение системы координат Oxyz, оси которой параллельны соответственно направлениям длины, ширины и высоты изображаемого предмета, (рис. 102).
Если известно, как искажаются размеры по осям x, y и z, то по чертежу можно судить о размерах предмета. Построенный таким образом чертеж называют аксонометрическим или аксонометрией.
Вторичные проекции
Для получения второй проекции на плоскости p a изображаемый объект предварительно проецируют на одну из координатных плоскостей. Затем полученную проекцию (вместе с осями координат) проецируют на плоскость p a . Сказанное поясняет рис. 104.
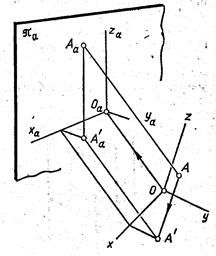
Рис. 104
Точка А (объект) спроецирована сначала на плоскость ХОУ. Полученную проекцию А' проецируют затем на плоскость p a . В конечном результате на аксонометрическом чертеже получаются два изображения точки А: А a и А' a (вторичная), которые вполне определяют ее положение относительно системы координат Oxyz .
Пример построения стандартных аксонометрических проекций
Обычно аксонометрические проекции оригиналов строятся по их комплексным чертежам. Рассмотрим несколько примеров построения стандартных аксонометрических проекций оригиналов, заданных своими комплексными чертежами.
Пример 1. Построить ортогональную изометрию шестигранной пирамиды.
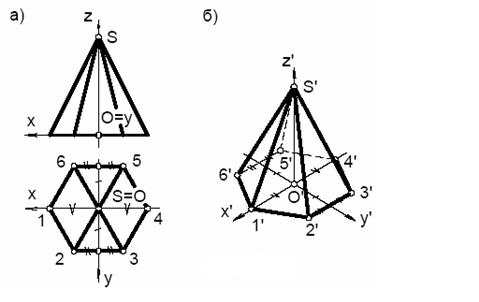
Рис. 109. Построение прямоугольной изометрии шестигранной пирамиды
Построение выполняем в следующей последовательности. Свяжем с пирамидой натуральную систему координат Oxyz. За начало координат выбираем точку О – центр основания пирамиды. Ось х направим влево (параллельно фронтальной плоскости), ось у – в сторону наблюдателя, ось z – вертикально вверх.
На свободном месте чертежа вычерчиваем аксонометрическую систему координат O ' x ' y ' z ', продлевая оси х и у в отрицательную сторону от точки О.
Для построения аксонометрии точек 1 и 4, лежащих на оси х, измеряем их абсциссы (координату х) и откладываем эти величины вдоль оси х' (с учетом отклонения относительно точки О). Напомним, что в приведенной изометрии показатели искажения по всем осям равны единице (т.е. размеры, измеренные на комплексном чертеже, непосредственно откладываются вдоль аксонометрических осей).
Точки 2,3,5 и 6 лежат на прямых, параллельных оси х. Поэтому удобно сначала построить эти вспомогательные прямые, расположенные на равных расстояниях от оси х (отмечены одним штрихом). Измерив на комплексном чертеже абсциссы указанных точек, откладываем полученную величину (отмечена двумя штрихами) на вспомогательных прямых от пересечения последних с осью у. Таким образом, построены все шесть точек основания пирамиды. Соединив точки основания, получаем изометрию шестиугольника.
Отложив на оси z от точки О высоту пирамиды, получим изометрию вершины S. Соединяя вершину пирамиды с шестью точками основания, получаем изометрию пирамиды. В заключении определяем видимость ребер пирамиды.
Пример 2. Построить стандартную ортогональную диметрию шестиугольной призмы с цилиндрическим отверстием, (рис. 110).
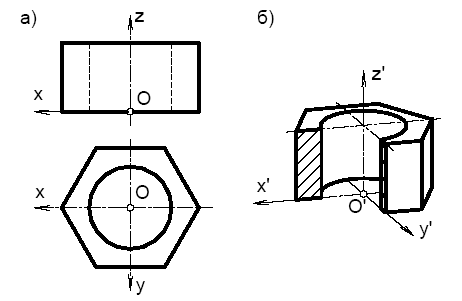
Рис. 110. Построение прямоугольной диметрии шестиугольной призмы
«Свяжем» с призмой натуральную систему координат Oxyz, расположив оси, как показано на рисунке 110а. Построим диметрические оси координат.В нашем примере деталь имеет две параллельные горизонтально расположенные плоскости. Сначала построим диметрические изображения окружности и шестиугольника, лежащих в нижней плоскости (xOy). Затем, отмерив высоту призмы вдоль оси z, вновь проведем диметрические оси и на этом уровне. Построим снова диметрические изображения окружности и шестиугольника, теперь уже лежащих в верхней плоскости детали. Соединим вертикальными отрезками полученные изображения – это и будет диметрия данной детали.
Часто для увеличения наглядности выполняют вырез части детали как это показано на рисунке 110б. В нашем примере секущие плоскости совпадают с координатными аксонометрическими плоскостями x ' O ' z ' и y ' O ' z '.
ВОПРОСЫ ДЛЯ САМОПОДГОТОВКИ:
1. Для чего нужны наглядные изображения предметов?
2. Назовите способы построения наглядных изображений?
3. Как получают аксонометрический чертеж?
4. Что такое коэффициент искажения в аксонометрии?
5. Какие виды аксонометрии вы знаете?
6. Чем характеризуется прямоугольная изометрия?
7. Чем характеризуется прямоугольная диметрия?
8. Какие правила вы знаете по определению направления большой оси эллипса в изометрии и диметрии?
9. Чему равна большая и малая оси эллипса в изометрии и диметрии.
ЛИТЕРАТУРА
1. Бубенников А.В. Начертательная геометрия: Учеб. для вузов. – 3-е изд., перераб. и доп. – М.: Высш. шк., 1985 – 288с. . ил.
2. Бубенников А.В. Начертательная геометрия: Задачи для упражнений: Учебн. пособие. – М.: Высш. шк., 1981 – 296с. ил.
3. Виницкий И.Г. Начертательная геометрия. Учебник для вузов. М.: Высш. шк., 1975.- 280 с.
4. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии: Учеб. пособие для втузов /Под ред. В.О. Гордона и Ю.Б. Иванова. – 24-е изд., стер. –М.: Высш. Шк., 2000. – 272 с.
5. Королев Ю.И. Начертательная геометрия: Учеб. для вузов.- М.: Стройиздат, 1987.- 319 с.: ил.
6. Климухин А.Г. Начертательная геометрия: Учебник для вузов. - 2-е изд., перераб. и доп. - М.: Стойиздат, 1978 - 334с.
7. Лагерь А.И., Колесникова Э.А. Инженерная графика / Учеб. для инж.-техн. спец. Вузов.- М.: Высш. шк., 1985 – 176 с.
8. Михайленко В.Е., Пономарев А.М. Инженерная графика: Учебник. – 3-е изд., перераб. и доп. –К.: Выща шк., 1990. – 303 с.
9. Нарисна геометрія: Підручник / В.С. Михайленко, М.Ф. Свстіфесв,
С.М. Ковальов, О.В. Кащенко; За ред. В.С. Михайленка. –2-ге вид.,
переробл. –К.: Вища шк., 2004. –303 с.
10. Начертательная геометрия: Учеб. Для вузов/ Н.Н. Крылов, Г.С. Иконникова, В.Л. Николаев, Н.М. Лаврухина; Под ред. Н.Н. Крылова.- 6 изд., пепераб. И доп.- М.: Высш. шк.,1990.-240 с.:ил.
11. Павлова А.А. Начертательная геометрия: Учебник для студентов педагогических институтов по специальности №03.02 (2120) «Труд» («Общетехнические дисциплины и труд»).- М.: Прометей 1993. 280с.: ил.
12.Стандарты Единой системы конструкторской документации.
13. Фролов С.А. Начертательная геометрия: Учебник для втузов. – М.: Машиностроение, 1978 – 240 с.
14. Чекмарев А.А. Начертательная геометрия и черчение: Учеб пособие для студентов пед. ин-тов по спец. №2120 «Общетехн. дисциплины и труд». – М.: Просвещение 1987. – 400 с.: ил.
15. Чекмарев А.А. Инженерная графика: Учеб для немаш. спец. вузов.- 2-е изд., испр. – М.: Высш. шк. 1998. – 365 с.
СОДЕРЖАНИЕ
Введение.............................................................................................................. 3
Принятые обозначения и символика.................................................................. 4
Лекция № 1. Способы проецирования. Точка и прямая на комплексном чертеже.............................................................................................................................. 5
1.1. Предмет начертательной геометрии. Способы проецирования............... 5
1.2. Инварианты ортогонального проецирования............................................ 7
1.3. Точка на комплексном чертеже................................................................... 9
1.4. Прямая на комплексном чертеже.............................................................. 10
1.4.1. Прямая общего положения на комплексном чертеже .......................... 10
1.4.2. Прямые частного положения.................................................................. 11
Вопросы для самоподготовки.......................................................................... 13
Лекция №2. Прямые и плоскости на комплексном чертеже............................ 14
2.1. Определение натуральной величины отрезка прямой и углов ее наклона к плоскостям проекций........................................................................................ 14
2.2. Взаимное положение двух прямых в пространстве................................. 15
2.3. Проецирование прямого угла................................................................... 16
2.4. Плоскость на комплексном чертеже.......................................................... 17
2.4.1. Способы задания плоскости на комплексном чертеже ......................... 17
2.4.2. Прямая и точка в плоскости................................................................... 17
2.4.3. Линии уровня плоскости......................................................................... 18
2.4.4. Плоскости частного положения.............................................................. 19
Вопросы для самоподготовки.......................................................................... 20
Лекция № 3. Взаимное положение двух плоскостей, прямой линии и плоскости............................................................................................................................ 21
3.1. Взаимное положение плоскостей............................................................... 21
3.2. Взаимное положение прямой лини и плоскости....................................... 23
3.3. Параллельные и взаимно перпендикулярные плоскости......................... 25
Вопросы для самоподготовки.......................................................................... 26
Лекция № 4. Способы преобразования комплексного чертежа..................... 27
4.1. Способ замены плоскостей проекций........................................................ 27
4.2. Плоскопараллельное перемещение........................................................... 30
Вопросы для самоподготовки.......................................................................... 32
Лекция № 5. Поверхности. Точки на поверхностях. Сечение поверхностей плоскостями.............................................................................................................. 33
5.1. Точки на поверхностях многогранников.................................................. 33
5.2. Точки на поверхностях тел вращения....................................................... 33
5.3. Пересечение многогранника плоскостью.................................................. 34
5.4. Сечения поверхностей вращения.............................................................. 35
5.4.1. Сечение цилиндра плоскостью............................................................... 35
5.4.2. Сечение конуса плоскостью.................................................................... 36
5.4.3. Сечение сферы плоскостью..................................................................... 37
5.4.4. Сечение тора плоскостью....................................................................... 37
Вопросы для самоподготовки.......................................................................... 38
Лекция № 6. Построение точек пересечения прямой с поверхностью........... 39
6.1. Общие положения...................................................................................... 39
6.2. Построение точек пересечения прямой с поверхностью многогранника 39
6.3. Построение точек пересечения прямой с поверхностью цилиндра......... 40
6.4. Построение точек пересечения прямой с поверхностью конуса.............. 42
6.5. Построение точек пересечения прямой со сферой................................... 43
Вопросы для самоподготовки.......................................................................... 44
Лекция № 7. Построение линии взаимного пересечения кривых поверхностей 45
7.1. Общие положения...................................................................................... 45
7.2. Способ вспомогательных секущих плоскостей........................................ 45
7.3. Соосные поверхности вращения............................................................... 47
7.3.1. Примеры соосных поверхностей вращения.......................................... 47
7.3.2. Примеры соосных поверхностей вращения, одна из которых сфера.. 48
7.3.3. Пересечение соосных поверхностей вращения в элементах конструкций 48
7.4. Способ вспомогательных сфер.................................................................. 49
7.4.1. Способ концентрических сфер............................................................... 50
7.4.2 Алгоритм способа концентрических сфер.............................................. 50
Вопросы для самоподготовки.......................................................................... 53
Лекция № 8. Метрические задачи..................................................................... 54
8.1. Общие положения...................................................................................... 54
8.2. Теоретические основы для решения метрических задач.......................... 54
8.3. Задачи на определение расстояний между геометрическими фигурами. 55
8.4. Задачи на определение действительных величин углов между плоскими геометрическими фигурами................................................................................... 60
8.5. Задачи на определение действительных величин плоских геометрических фигур...................................................................................................................... 63
8.6. Задачи на построение в плоскости общего положения геометрических фигур по заданным размерам..................................................................................... 64
Вопросы для самоподготовки.......................................................................... 65
Лекция № 9. Аксонометрические проекции..................................................... 66
9.1. Общие положения...................................................................................... 66
9.2. Аксонометрические оси и показатели искажения..................................... 67
9.3. Вторичные проекции................................................................................. 68
9.4. Виды аксонометрических проекций.......................................................... 68
9.5. Прямоугольные аксонометрические проекции......................................... 69
9.6. Стандартные аксонометрические проекции.............................................. 69
9.7. Построение в прямоугольной аксонометрии окружности, расположенной в плоскости, параллельной одной из плоскостей проекций.............................. 70
9.8. Пример построения стандартных аксонометрических проекций............ 71
Вопросы для самоподготовки.......................................................................... 73
Литература........................................................................................................ 74
Учебное издание
Конспект лекций по курсу начертательная геометрия (для студентов заочной формы обучения всех специальностей академии)
Составитель: Владимир Иванович Лусь
Редактор Н.З. Алябьев
План 2007, поз.
Подп. к печати 20.03.2007 Формат 210´297 1/8 Бумага офисная
Печать на ризографе Усл.-печ. л. Учет.-изд.л.
Тираж 150 экз. Заказ. №
61002, Харьков, ХНАГХ, ул. Революции, 12
Сектор оперативной полиграфии ИВЦ ХНАГХ
61002, Харьков, ХНАГХ, ул. Революции, 12
По курсу
Начертательная геометрия
(для студентов заочной формы обучения
всех специальностей академии )

Харьков – ХНАГХ - 2007
Конспект лекций по курсу начертательная геометрия (для студентов заочной формы обучения всех специальностей академии). Сост. Лусь В.И.
– Харьков: ХНАГХ, 2007. – 79 с.
Составитель: В.И. Лусь
Рекомендовано кафедрой инженерной и компьютерной графики, протокол № 7 от 28 февраля 2007 г.
 |
ВВЕДЕНИЕ
В число дисциплин, составляющих основу инженерного образования, входит начертательная геометрия.
Предметом начертательной геометрии является изложение и обоснование способов построения изображений пространственных форм на плоскости.
Изображения, построенные по правилам, изучаемым в начертательной геометрии, позволяют представить мысленно форму предметов и их взаимное расположение в пространстве, определить их размеры, исследовать геометрические свойства, присущие изображаемому предмету.
Начертательная геометрия развивает пространственное воображение и передает ряд своих выводов в практику выполнения чертежей, обеспечивая их выразительность и точность, а, следовательно – и возможность изготовления по этим чертежам изделий. Овладение чертежом как средством выражения технической мысли и как производственным документом происходит на протяжении всего процесса обучения в ВУЗе при изучении общеинженерных и специальных дисциплин, а также при выполнении курсовых и дипломных проектов.
В курсе лекций рассмотрение метода проекций начинается с построения проекций точки, так как при построении изображения любой пространственной формы рассматривается ряд точек, принадлежащих этой форме.
Сегодня одним из направлений перестройки высшей школы является усиление самостоятельности, предоставляемой студентам при изучении той или иной дисциплины. Правильно построенные самостоятельные занятия по начертательной геометрии разрешат трудности в изучении этой дисциплины.
Для повторения и закрепления изучаемого материала, в целях самопроверки, к материалу каждой лекции имеется значительное число вопросов, на которые необходимо ответить.
Указана учебная литература, для желающих ознакомиться с различными вариантами изложения разделов программы и с некоторыми дополнительными вопросами начертательной геометрии.
ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ И СИМВОЛИКА
1. Г, Δ¸ Σ¸ Π¸ Λ¸ Ψ¸ Ф, Ω – поверхности (плоскости)
2. П1, П2, П3 – основные плоскости проекций
3. П4, П5, …. – дополнительные плоскости проекций
4. a , b , c , …- линии в пространстве
5. А, В, С, …, 1, 2, 3, … - точки в пространстве
6. a ¸ β¸ γ¸ φ – углы
7. А1, А2, А3,…, а1, а2, а3, …, Г1, Г2, Г3, … - проекции точек, линий, поверхностей на плоскости проекций
8. (АВ) – прямая, проходящая через точки А и В
9. [AB] – отрезок прямой
10. |AB| - Расстояние между точками А и В
11. çç - параллельность
12. ^ - перпендикулярность
13. ║ - непараллельность
14.  ^ - неперпендикулярность
^ - неперпендикулярность
15.  ------ - скрещивание
------ - скрещивание
16. = - равенство, результат
17. º - тождественность
18. Î принадлежность
19. Ì - включение
20. Ç - пересечение
21. @ - конгруэнтность
22. ® - преобразование, отображение
23. Ù - логическое «и»
24. Ú - логическое «или»
25. Þ - логическое следование
26. Û - эквивалентность
Дата: 2019-02-02, просмотров: 359.