Теорема 4 (о ”наименьшем” целом числе). Всякое непустое, ограниченное снизу множество целых чисел соДержит наименьшее уисло. (Здесь, как и в случае натуральных чисел, слово ” множество“ используется вместо слова ”подмножество“ Э
Д о к а з а т е л ь с т в о. Пусть О А С Z и А ограничено снизу, т.е. 36 ? ZVa ? А(Ь < а). Тогда если Ь Е А, то Ь— наименьшее число во множестве А.
Пусть теперь Ь А.
Тогда Уа е Аф < а) и, значит, Уа А(а — Ь > О).
Образуем множество М всех чисел вида а — Ь , где а пробегает множество А , т.е. М = {с [ с = а — Ь, а Е А} 
Очевидно, что множество М не пусто, поскольку А 74 0 
Как отмечено выше, М С N . Следовательно, по теореме 
н а т у р ал ь н о м ч и с л е (54, гл.Ш) во множестве М существует наименьшее натуральное число т. Тогда т = а1 — Ь для некоторого числа а1 ? А, и, поскольку т наименьшее в М, то Уа ? А(т < а — Ь) , т.е. 
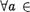А (01 — Ь < а — Ь). Отсюда Уа е А(а1 а), а так как ат (- А , то — наименьшее число в А. Теорема доказана.
Теорема 5 (о “ наибольшем“ целом числе). Всякое непустое, ограниченное сверсу множество целыс чисел соДержит наибольшее число.
Д о к аз а те ль с т во . Пусть О 74 А С Z и А ограничено сверху числом Ь, т.е. ? ZVa е А(а < Ь). Тогда —а > Ь для всех чисел а ? А.
Следовательно, множество М {с г = —а, а ? А} не пусто и ограничено снизу числом (—6). Отсюда по предыдущей теореме во множестве М сицествует наименьшее число, т.е. ас ? МУс ? М (с < с).
Это означает, что Уа ? А(с < —а), откуда Уа ? А(—с > а) 
Далее, поскольку с (- М , то с = —ао для некоторого числа ао ? А, откуда в силу предыдущего высказывания следует Уа ? А(ао > а) и, значит, ао — наибольшее число в А. Теорема доказана.
З. Различные формы метода математической индукции для целых чисел. Теорема о делении с остатком
Теорема 1 (первая форма метода математической индукции). Пусть Р(с) — оДноместныб преДикат, опреДеленный на множестве Z целых чисе.,4 . ТогДа если Для некоторого ЧИСЛа а Z преДложение Р(о)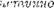 
и Для произвольного целого числа К > а из Р(К) слеДует Р(К -4- 1), то преДложение Р(г) справеДлиео Для всес целы,т чисел с > а (т.е. на множестве Z является истинной следующая формула исчисления предикатов:
Р(а) лук > 
+ 1)) Ус > аР(с)
для любого фиксированного целого числа а 
Д о к а з а т е л ь с т в о. Пусть для предложения Р (с) верно все, о чем говорится в условии теоремы, т.е.
1) Р(а) — истинно;
2) УК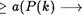 
Щ к + также истинно.
От противного. Предположим, что найдется такое число
Ь > а, что РФ) — ложно. Очевидно, что Ь а , поскольку Р (а) истинно. Образуем множество М = {z ? > а, P(z)— ложно}.
Тогда множество М 0 , поскольку Ь ? М и М— ограничено снизу числом а. Следовательно, по теореме о н а и м е н ьш е м ц е л о м ч и с л е (теорема 4, 2) во множестве М существует наименьшее целое число с. Отсюда с > а, что, в свою очередь, влечет с — 1 > а.
Докажем, что Р(с—1) — истинно. Если с—1 = а, то Р (с— 1) истинно в силу условия.
Пусть с— 1 > а. Тогда предположение, что Р(с— 1) — ложно, влечет принадлежность с 1 ? М, чего не может быть, поскольку число с— наименьшее во множестве М.
Таким образом, с — 1 > а и Р(с — 1) — истинно.
Отсюда в силу условия данной теоремы предложение Р((с— 1) + 1) — истинно, т.е. Р(с) — истинно. Это противоречит выбору числа с , поскольку с ? М 
Теорема доказана.
Заметим, эта теорема обобщает следствие 1 из аксиом Пеано.
Теорема 2 (вторая форма метода математической индукции для целых чисел). Пусть Р(с) — некоторый оДноместный преДшсатп, опреДеленньи) на множестве Z целыс чисел. ТогДа если преЭложение Р (с) справеДливо Для некоторого целого числа К и Для произвольного Цело•го числа s К из справеДливости преДложения Р(с) Для всес целых чисел, , уДовлетворяющис неравенству К < с < s, слеДует справеДливость этого преДложения Для числа s , то это преДложение справеДливо Для всег целыс чисел с > К.
Доказательство этой теоремы во многом повторяет доказательство аналогичной теоремы для натуральных чисел (теорема 1, 55, гл.Ш).
Теорема З (третья форма метода математической индукции). Пусть Р(с) — оДноместньиЈ преДикат, опреДеленный на множестве Z целыс ЧИСи. ТогДа если Р(с) истинно Для всес чисел некоторого бесконечного поДмножества М множества натуральных чисел и Для произвольного целого числа а из истинности Р(а) слеДует истинность Р (а — 1) , то преДложение Р(с) справеДливо Для всес целыс чисел.
Доказательство аналогично доказательству соответствукощей теоремы для натуральных чисел.
Предлагаем его в качестве интересного упражнения.
Заметим, что в практике применения третья форма математической индукции встречается реже, чем остальные. Это объясняется тем, что для ее применения необходимо знать бесконечное подмножество М множества натуральных чисел“ , о котором говорится в теореме. Нахождение такого множества может оказаться нелегкой задачей.
Но преимущество третьей формы перед остальными заключается в том, что с ее помощью предложение Р(с) доказывается Для всес целыс чисел.
Ниже мы приведем интересный пример применения третьей формы“ . Но сначала дадим одно очень важное понятие.
Определение. Абсолютной величиной целого числа а называется число , опреДеленное по правилу
0, если а 
О а, если а > О
—а, если а < 0.
Таким образом, если а 0 , то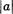 
? N.
Предлагаем читателю в качестве упражнения доказать следующие свойства абсолютной величины:
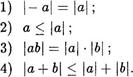
Теорема (о делении с остатком). Для любыс целыс чисел а и Ь, где Ь 0, существует и притом только одна пара чисел q U т таких, что а г: bq+T Л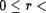 
Д.
Д о к аз а т е л ь с т в о.
1. Существование пары (q, т).
Пусть а, Ь ? Z и 0. Покажем, что существует пара чисел q и , удовлетворяющих условиям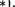 
Доказательство проведем индукцией в третьей форме по числу а при фиксированном числе Ь .
М = {mlm= n• lbl,n? N}.
Очевидно, что М С лт отображение f : N М, определенное по правилу f(n) = nlbl для любого п ? N, является биекцией. Это означает, что М N, т.е. М— бесконечно.
Докажем, что для произвольного числа а ? М (и Ь— фикси 
рованного) утверждение теоремы о существовании пары чисел q и т верно.
Действительно, пусть а (- М . Тогда а пф! для некоторого п ? N.
Если Ь > 0, то а = пь + О. Полагая теперь q = п и т О, получаем требуемую пару чисел q и т. Если же Ь < 0, то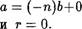 
и, значит, в этом случае можно положить q 
Сделаем теперь инДуктпиеное преДположение. Допустим, что для произвольного целого числа с (и произвольного фиксированного Ь 0 ) утверждение теоремы верно, т.е. существует пара чисел (q, т) такая, что
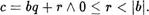
Докажем, что оно верно и для числа (с 1) . Из равенства с = bq -4- следует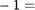 
bq + (т — 1). (1)
Возможны случаи.
1) т > 0. Тогда 7' — 1 > 0. В этом случае, положив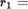 
— т — 1, получим с — 1 — bq + Tl, где пара (q, 7'1,) очевидно удовлетворяет условию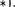 
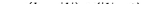0. Тогда с — 1 bq1 + 711 , где q1
Без труда докажем, что 0 < < Д.
Таким образом, утверждение верно и для пары чисел
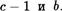
Первая часть теоремы доказана.
П. ЕДинственность пары q и т.
Предположим, что для чисел а и Ь 0 существуют две пары чисел (q, т) и (q1, то, удовлетворяющие условиям (*) 
Докажем, что они совпадают. Итак, пусть
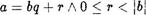
и а bq1 Л О < Д.
Отсюда вытекает, что b(q1 —q) т— 71 1. Из этого равенства следует, что
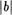• iql - 
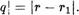(2)
Если теперь допустить, что q ql , то q — q1 0, откуда lq — q1l 1. Умножая эти неравенства почленно на число lbl, получим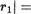 
ф! • - q11 Д. (3)
В то же время из неравенств 0 < т < lbl и О < < очевидным образом следует — < ф!. Это противоречит (3). Теорема доказана.
У п р а ж н е н и я:
1. Завершите доказательства теорем 2 и З из 5 1.
2. Докажите следствие 2 из теоремы З, 1.
3. Докажите, что подмножество Н С Z, состоящее из всех чисел вида < п + 1, 1 > (п ? N), замкнуто относительно сложения и умножения.
4. Пусть Н означает то же множество, что и в упражнении 3. Докажите, что отображение ј : М удовлетворяет условиям:
1) ј — биекция;
2) ј(п + т) = ј(п) + j(m) и j(nm) = ј(п) • j(m) для любых чисел п, т (т.е. ј осуществляет изоморфизм алгебр (N, 4, и (Н, + , ).
5. Завершите доказательство теоремы 1 из 2.
6. Докажите, что для любых целых чисел а, Ь, с справедливы импликации:
7. Докажите вторую и третью теоремы из З.
8. Докажите, что кольцо Z целых чисел не содержит делителей нуля.
Литература
1. Бурбаки Н. Теория множеств. М.: Мир, 1965.
2. ВинограДов И. М. Основы теории чисел. М.: Наука, 1972. З. ДемиДов И. Т. Основания арифметики. М.: Учпедгиз, 1963.
4. Каргаполов М. И., Мерзляков Ю. И. ОсНОвы теории групп.
М.: Наука, 1972.
5. Кострикин А. И. Введение в алгебру. М.: Наука, 1994.
б. Куликов Л. Я. Алгебра и теория чисел. М.: Высш. шк., 1979.
7. Курош А.Г. Курс высшей алгебры. М.: Наука, 1971.
8. Любецкий В. А. Основные понятия школьной математики. М.: Просвещение, 1987.
9. Ляпин ЕС. и др. Упражнения по теории групп. М.: Наука, 1967.
10. Мальцев А. И. Алгебраические системы. М.: Наука, 1970.
11. МенДельсон Э. Введение в математическую логику. М.: Наука, 1971.
12. Нечаев В. И. Числовые системы. М.: Просвещение, 1975.
13. Новиков П.С. Элементы математической логики. М.. Наука, 1973.
14. Петрова В. Т. Лекции по алгебре и геометрии.: В 2 ч.
ЧЛ. М.: Владос, 1999.
15. Современные основы школьного курса математики 
Авт. кол: Виленкин Н.Я., Дуничев К.И., Каллтжнин ЛА 
Столяр А.А. М.: Просвещение, 1980.
16. Скорняков Л. А. Элементы алгебры. М.: Наука, 1980.
17. Стом Р.Р. Множество, логика, аксиоматические теории. М.; Просвещение, 1968.
18. Столяр А. А. Логическое введение в математику. Минск: ВЫШЭЙШ. шк., 1971.
19. Филиппов В. П. Алгебра и теория чисел. Волгоград: вгпи, 1975.
20. Френкел А., Бар-Хилел И. Основания теории множсств. М.: Мир, 1966.
21. Фукс Л. Частично упорядочные системы. М.: Мир, 1965.
Учебное изДание
Владимир Константинович Карташов
ВВОДНЫЙ КУРС МАТЕМАТИКИ
Учебное пособие
Редакционная подготовка О. И. Молокановой Оригинал-макет подготовил А. П. Бощенко
„ПР 020048 от 20.12.96 г.
Подписано к печати 28.08.99 г. Формат 60х84/16. Печать офс. Бум. тип. М 2. Уел. печ. л. 8,2. Уч.-изд. л. 8,3. Тираж 500 экз. Заказ 2
Издательство «Перемена»
Типография издательства «Перемена»
400005. Волгоград, пр. им. В. И. Ленина, 27. ВГ ПУ
Дата: 2019-02-02, просмотров: 343.
