Определение. Пусть — произвольное отношение эк:в ивалентности на множестве Х и а ? Х . ТогДа классом Ка эквивалентности с порожДающим элементом а называется множество всес элементов с ? Х , эквивалентныс элементу а, т.е.
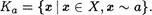
Классы эквивалентности облаДают следующими свойствами:
1. ПорожДающиб элемент а принаДлежит классу Ка.
2. Если Ь е ка , то Ю = ка,
т. е. любой элемент из класса эквивалентности может быть выбран в качестве порожДающего элемента. З. Для любыс элементов а, Ь Х
Другими словами, массы эквивалентности совпаДают тогДа и только тогДа, когДа ис порожДающие элементы эквивалентны.
4. Любые Два класса эквивалентности либо равны, либо не тьиеют общих элементов. Это свойство, очевидно, равносИЛьно следующему:
Уа, ь е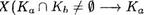 
= ко.
5. Множество Х , на котором заДано некоторое отношеэквивалентности, равно объеДинению всес классов этой эквивалентности, т.е.
Х = Uaexka.
Д о к а з а т е л ь с т в о.
Первое свойство, очевидно, следует из рефлексивности
Свойство 2. Пусть Ь ? Ка . Покажем, что Кь = Ка 
Пусть с ? Кь . Тогда с Ь . В то же время из Ь ? Ка следует Ь а. 1 еперь из с Ь и Ь а по свойству транзитивщх:ти отношения эквивалентности получим с а и, значит, с Е Ка . Этим доказано включение Кь С Ка 
Обратно, пусть с е Ка . Тогда с а. Поскольку Ь а , то в силу симметричности а Ь , откуда ввиду с а и свойства транзитивности следует г Ь , т. е. с Кь . Таким образом, Ка С Кь . Следовательно, Ка = Кь . 
Свойство З. Импликация
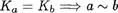
очевидна ввиду свойства 2.
Обратно, если а Ь, то а ? Кь, откуда по свойству 2 вытекает равенство Ка = Кь .
Свойство 4. Пусть Ка П Кь О для некоторых а, Ь ? Х 
Тогда существует элемент с ? Х такой, что с ? Ка и с ? Кь одновременно.
Из принадлежности с ? Ка по свойству 2 имеем Кс = Ка 
Аналогично из с ? Кь получим Кс = Кь. Следовательно, ка = кь .
Свойство 5. Из свойства 1 следует, что каждый элемент Множества Х содержится в некотором классе эквивалентности. Это означает, что Х С (Лех Ка .
С другоЙ стороны, очевидно, что l._Ja?xka С Х , поскольку
Каждый класс Ка включается в Х 
Будем говорить, что семейство {Xi i I} подмножеств образует разбиение этого множества на классы Xi если:
1) все поДмножества (тслассы) Xi не пусты;
2) любые Два различныс поДмножества Xi и Х) не пересетсаются (т.е. Xi П Х5 = О) •
З) объеДинение всес татсис поДмножеств есть множество х, т.е. Х =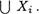 
Например, множество А = {1, 2, З, 4, 5} можно разбить на классы „41 = {1} , „42 = {2, 5}, Аз = {З, 4} ; множество целыс чисел Z можно разбить на классы нечетных Чисел Х1 
{qiq 2k + Z} и четныс чисел Х2 = {z — 2k, к е т.
Следующая теорема указывает на важную связь между понятиями ”.эквивалентность” и “разбиение ” 
Теорема З. Классы любой эквивалентности на множестве Х образуют разбиение этого множества. Обратно, Для кажДого разбиения на множестве можно опреДелить эквивалентность на этом множестве так, что ее массы образуют исходное разбиение.
Д о к а з а т е л ь с т в о.
1. Пусть на множестве Х задана эквивалентность . Покажем, что все различные классы этой эквивалентности образуют разбиение множества Х .
Действительно, свойство 1) разбиения вытекает из свойства 1 классов эквивалентности.
Свойство 2) разбиения выполняется ввиду свойства 4 для классов эквивалентности.
И, наконец, свойство 3) разбиения имеет место в силу свойства 5 для классов эквивалентности.
Итак, первое утверждение теоремы доказано.
П. Обратно, пусть на множестве Х задано разбиение, т. е. семейство {Xi i е I} подмножеств множества Х , удовлетворяющих условиям 1) — З).
Определим на множестве Х бинарное отношение по правилу: cFy тогда и только тогда, когда элементы принаДлежат оДному и тому же поДмножеству Данного разбиения. Другими словами, cFy 3i ? Xi Л у ? Xi).
Легко проверяется, что отношение F является эквивалентностью.
Покажем теперь, что классы этой эквивалентности есть е точности подмножества Данного разбиения.
Пусть Ка — какой-нибудь класс эквивалентности Р. Тогда, по определению, существует подмножество Xi(i е I) данного разбиения такое, что а Х; . Это означает, что любой элемент 
е Х; находится в отношении F с элементом а и, значит, л с ка 
Обратно, пусть с ? Ка. Тогда cFa, откуда, по определению, элементы с и а принадлежат оДновременно некоторому подмножеству Xi(i ? Т) данного разбиения.
Отсюда, поскольку по определению разбиения кажДьиЈ элемент множества Х принаДлежит только оДному поДмножеству разбиения и а ? Xi, то с ? Х; и, значит, Ка = Xi. 
Таким образом, показано, что каждый класс эквивалентности F совпадает с некоторым подмножеством данного разбиения.
Обратно, взяв произвольное подмножество Xi(i Т) данного разбиения множества Х , мы замечаем, что Х; С Ка для любого фиксированного элемента а Xi . Повторяя теперь дословно предыдущие рассуждения, получим, что Х; Ка 
Теорема доказана.
Определение. Фактор-множеством множества Х по отношению эквивалентности называется множество, каж-• дый элемент которого является одним из классов эквивалентности. Обозначается фактор-множество символом Х[Р .
П р и м е р. Пусть Х = {(р, q) lq О, p,q Z} . Отношение F на множестве Х определим по правилу:
(р, q) (И, ф), тогДа и только тогДа, если pq1 = P1q.
Тогда фактор-множество X/F можно рассматривать как Множество рациональных чисел. При этом рациональное число определяется как класс эквивалентности , т.е. семейство пар (р, q) , q 0, где при pql — Plq О две пары (р, q) и (21, q1) определяют одно и то же рациональное число.
11. Операции на множестве
Рассмотрим конечное множество А {а, Ь, с, d,e} и зададим отображение множества А в А с помощью следующей таблицы:
Приведенная таблица устанавливает соответствие между элементами множества А . В верхней строке ее записаны элементы множества А , а под каждым из них в нижней строке находится его образ. В этом случае говорят, что на множестве А задана унарная операция.
В алгебре часто изучаются операции, связывающие пары чисел с третьим числом. Такие операции называются бинарныли. Примерами бинарных операций являются: сложение, умножение на множестве R действительных чисел и другие.
Определение 1. Бинарной операцией на множестве А называется произвольное отображение
Таким образом, бинарная операция каждой упорядоченной паре (а, Ь) элементов множества А ставит в соответствие третий элемент с этого же множества, а именно, образ пары (а, Ь) ? А х А при отображении Т , т.е. с = Т Ь) ) . В практике последняя запись встречается редко. Как правило, вместо нее пишут:
с аТЬ и читают: ”элемент с есть результат операции Т над элементами а и Ь Вместо символа Т часто используется один из знаков + ” (сложение) или (умножение). В первом случае говорят об использовании аДДитивной терминологии, во втором — мультипликативной.
Результат операции называется, соответственно, суммой или произвеДением.
П ри м ер ы .
1. Сложение и умножение на каждом из множеств N, Z, Q 
R, где N, Z, Q, R обозначают, соответственно, множество натуральных, целых, рациональных и действительных чисел.
2. Возведение в степень на множестве натуральных чисел.
З. Объединение и пересечение на множестве подмножеств некоторого множества.
Ко н т р п р и м е р ы:
1. Вычитание на множестве N не является бинарной операцией, т.к. при вычитании из меньшего числа большего получаем число, не принадлежащее множеству N 
2. Умножение во множестве иррациональных чисел П 
R \ Q также не является бинарной операцией, т.к., например, • = 2 и число 2 
Пусть Е— множество с бинарной операцией Т и С Е 
Тогда, если результат операции над любыми двумя элементами из F также принадлежит F , то множество называется замкнутым относительно рассматриваемой операции Т .
Например, множество {с с 2k, К ? Z} четных целых чисел является замкнутым подмножеством относительно сложения и умножения на множестве Z. а множество иррациональных чисел О С R не является замкнутым подмножеством относительно операции умножения на множестве R.
По аналогии с понятием п-арного отношения (гл.П, 
можно обобщить определение операции на любое число аргументов:
пусть А— множество и п— фиксированное натуральное число. Тогда п-арной операцией на множестве А называется произвольное отображение Т : АП —» А ( АП А х 
декартово произведение п сомножителей, равных А 
Таким образом, всякая п -арная операция Т произвольному упоряДоченному набору (щ , (12, . Ч) из п элементов Данного множества А ставит е соответствие еДинственныт) элемент с Т (01, 02, . оп) этого множества.
Очевидно, что при п = 1 операция Т становится унарной, а при п 2— бинарной. Используется также термин 0-арная Операция. Говорят, что на множестве определена 0 -арная опеРация, если на этом множестве зафиксирован некоторый элемент е .
Заметим, что вместо фразы Т является п -арной операчиеТ' иногда говорят, что ” арность операции Т равна п 
Например, арность любой бинарной операции равна 2, унарной— 1 и т.д.
Аналогичное соглашение имеет место и для п -арных отношений .
Свойства бинарной операции
Ассоциативность. Бинарная операция Т называется ассоциативной, если аТ ФТС) = (атьрс для любых элементов а, Ь, с ? А 
Например, сложение и умножение во множестве натуральных чисел N ассоциативно, а возведение в степень — не ассоциативно, поскольку равенство (а ) = ab выполняется не для всех натуральных чисел. Например, (22 ) 3 223 
Коммутативность. Бинарная операция Т называется коммутативной, если аТЬ = ЬТа для любых а, Ь ? А .
Регулярный элемент. Элемент а называется регулярным относительно бинарной операции Т , если для любых с, у ? А, равенства аТс ату и гТа = ута влекут с = у . В этом случае говорят, что равенства можно сократить на а .
1. Относительно сложения во множестве действительных чисел R любое число регулярно.
2. 
Относительно умножения во множестве R регулярным является всякое число, кроме нуля, так, например, 0х2 = Ох 7 но 2 + 7 .
Нейтральный элемент. Пусть А — множество с бинарной операцией Т . Нейтральным элементом относительно операции Т называют такой элемент е ? А , что равенство еТс = СТе = с справедливо для любого с ? А 
Легко проверить, что если такой элемент существует, то он единственен. Нейтральный элемент, как видно из определения, регулярен.
Как правило, в аДДитивной терминологии нейтральный элемент называют нулем, а в мультипликативной — еДиницеб.
Например, во множестве целых чисел Z нейтральным элементом относительно сложения является число О , а число 1 служит нейтральньџа элементом относительно умножения.
Во множестве Р (А) всех подмножеств данного множества А пустое множество 0 выполняет роль нейтрального элемента относительно операции объединения.
Симметричные элементы. Пусть бинарная операция Т задана на множестве А , обладает нейтральным элементом е . Говорят, что элемент а! ? А симметричен элементу а ? А 
если ата = ата' е. (1)
В аддитивной терминологии симметричный элемент называется противоположным, а в мультипликативной — обратньии к данному.
1. Если а (- R , то число —а R является симметричным (противоположным) элементом относительно сложения. 
2. Если а ? R и а О , то число а— 1 Е R является симметричным (обратным) элементом относительно умножения.
З. Если е — нейтральный элемент, то его симметричным элементом служит он сам, т.к. еТе = е .
Из равенств (1) очевидным образом следует, что если элемент а' е А является симметричным к элементу а ?- А , то а симметричен к а' , т.е. (ау = а.
Следствие 1. Пусть А — множество с ассоциативной бинарной операцией Т и нейтральным элементом е . ТогДа любой элемент а ? А не может иметь более оДноео симметричного элемента.
Д о к а з а т е л ь с т в о. Пусть а1 и а2 — симметричные к а элементы относительно бинарной операции Т . По опреде-
лению, имеем
ата1 аса     
| (2) |
ата2 - ада    
| (3) |
Тогда, очевидно, аТа1 = аТа2, откуда а1Т(аТа1) = а1Т(аТа2). Отсюда, в силу ассоциативности операции Т, получим
(01Та)Т01 — (а1Та)Та2 . Теперь из (2) следует, что еТа1 
еТа2 и, значит, ат = 02 .
Дистрибутивность. Пусть на множестве А определены две бинарные операции Т и Ш. Говорят, что операция Т Дистрибутивна относительно операции Ш , если для любых а, Ь, с имеет место aT(b с) (ато (атс).
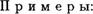
1. На множестве действительных лисел R умножение дистрибутивно относительно сложения:
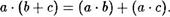
Однако сложение не дистрибутивно относительно умножения.
2. Для операций объединения и пересечения подмножеств произвольного универсального множества справедливы равенства:
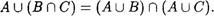
Следовательно, кажДая из этис операций Дистрибутивна относительно Другой.
512. Понятие об алгебраической системе.
Алгебры и модели. Классические примеры алгебр. Изоморфизм алгебр
Пусть А — произвольное множество. В дальнейшем это множество будем называть основным или носителем (построенной) алгебраической системы. Зафиксируем на носителе А некоторые операции F1 , . , Fk и отношения (предикаты)
Пусть тк арность операции Fi(i — К) и тэ— арность отношения Р) (ј 1, s). Положим далее {F1, . 
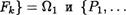, Рз} = 02.
Дата: 2019-02-02, просмотров: 306.
