Так же, как и для сложения, из опреДеления и теоремы существования и еДинственности умножения вытекают свойства:
1) а • 1 = а Для любого а N.
2) а • Ы = ab + а Для любыс чисел а, Ь N. З) 1 • а = а Для любого а ? N.
4) а!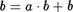 
Для любыс a,b G N.
5) Умножение натуральныс чисел коммутативно:
аЬ = ba
Для любыс чисел а, Ь ? N.
Д о к а з а т е л ь с т в о свойства 5 проведем инДутсцией по Ь (при фиксированном числе а ). Пусть Ь = 1. Тогда утверждение вытекает из свойств 1) и З). Предположим, что равенство (14) имеет место при Ь = п, т.е. ап = па. Пусть Ь = . Тогда аж ап+а по свойству 2, откуда в силу индуктивного предположения ап' = па + а . Поскольку па + а тва в силу свойства 4, то ап' = п'а . Это означает, что равенство
(14) имеет место и при Ь п' . Утверждение доказано.
6) Умножение Дистрибутивно относительно СЛО.жениЯ.•
(а + ас + bc, (15)
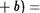са + сь
Для любыс натуральныс чисел а, Ь, с .
Д о к а з а т е л с т в о. В силу коммутативности умноженил Достаточно Доказать только тожДество (15). Доказательство будем вести инДукцией по с (при фиксированных
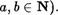
Пусть с 1 . Тогда (а + Ь) • 1 а + Ь по свойству 1. Применяя это свойство еще раз, получим а -4- Ь = а • 1 + Ь • 1 
откуда в силу предыдущего равенства следует, что (a+b) • 1 —
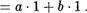
Предположим теперь, что формула (15) справедлива при с п, т.е. (а + ап+ bn.
Положим с = п!. Тогда в силу свойства 2 имеем (а+Ь)п' 
(а + + (а Ч- Ь), откуда по индуктивному предположению следует равенство (а + Ь)п' (ап + bn) + (а + Ь). Используя теперь свойства ассоциативности и коммутативности сложения,
получим
(а + b)nl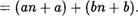 
По свойству 2 справедливы равенства
ап + а г: ап' и bn + Ь = bn. l
Отсюда с учетом предыдущего равенства окончательно имеем
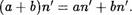
Это означает, что равенство (15) справедливо и при с Ы. Утверждение доказано.
7) Умножение ассоциативно, т.е.
(ab)c = a(bc) (16) Для любы.с натуральныс ЧИСЕЛ а, Ь, с .
Д о к а з а т е л ь с т в о проведем индукцией по с (при фиксированных а, Ь N ).
Пусть с 1 Тогда по свойству 1 имеем (ab) • 1 — ab и 
— Ь, откуда (ab) • 1 — a(b • 1), и, значит, в этом случае равенство (16) верно.
Предположим, что равенство (16) справедливо при с = п , т.е. (ab)n = a(bn) 
Пусть теперь с . Тогда по свойству 2 получим (ab)n' (ab)n + ab . Правая часть этого равенства в силу индуктивного предположения равна числу a(bn) 4- ab , которое в силу дистрибутивности умножения относительно сложения, в свою очередь, равно a(bn + Ь) . Это означает, что (ab)n' — — a(bn + Ь) .
Отсюда, поскольку bn+ Ь = bn' по свойству 2, то (ab)n' — — a(bn') , т.е. формула (16) верна и при с = п' . Утверждение доказано.
Заметим, что в доказательстве свойства 7 существенно используется дистрибутивность умножения натуральных чисел относительно сложения. Попытки доказать ассоциативность 
умножения сразу после доказательства свойства коммутативности или раньше оказались бы безуспешными .
5 З. Сравнение натуральных чисел
Определение. Пусть а, Ь N Будем говорить, что ” а меньше Ь если существует натуральное число и такое, что Ь а и 
Для обозначения отношения ” меньше“ используется знак
Таким образом, по определению,
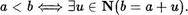
Ясно, что < является бинарным отношением. Ниже будет показано, что это отношение является отношением поряДк•а.
Свойства бинарного отношения ” меньше“. 1) Отношение ”меньше" антирефлексивно, т.е.
—(n < п) (каждое число п ? N не меньше самого себя).
Д о к а з а т е л ь с т в о проведем метоДом от противного. Предположим, что п п для некоторого числа п . Тогда, по определению, существует такое число и ? N, что п = п + и, откуда по аксиоме Р2 справедливо равенство п! (п+и)', что, по свойству 2 сложения, в свою очередь, влечет п! п + Т, т.е. п А- 1 = п + Ы. Применяя теперь закон сокращения, получим и' = 1 , что противоречит аксиоме а. Утверждение доказано. 2) Отношение “меньше“ транзитивно, т.е.
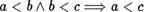
для любых чисел а, Ь, с N 
Д о к а з а т е л ь с т в о. Пусть а Ь и Ь с. Тогда
Ь + для некоторых чисел и, 1) . Отсюда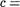 
(а + и) +v а + (u+v), что влечет а < с по определению.
Таким образом, отношение ” меньше“ является строгим поряДком.
З) Для любого натурального числа п справеДливо п < п! 
Это утверждение очевидно,поскольку п!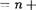 
4) ЕДиница меньше любого натурального числа, отличного от нее, т.е.
Действительно, если п 1 , то по следствию 2 из аксиом Пеано п = т! для некоторого числа т , откуда, ввиду свойств 1 и З сложения п 1 + т. Это означает, что 1 п . 5) Сложение натуральныс ЧИссЛ монотонно, т.е.
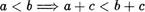
для любых натуральных чисел а, Ь, с .
Заметим, что это свойство иногда формулируют следующим образом: ” Отношение меньше стабильно относительно слоэюения 
Д о к аз а т е л ь с т в о. Пусть а < Ь . Тогда по определению существует число и такое, что Ь = а + и. Отсюда Ь + с — = (а + и) + с (а + с) + и. Это означает, что а + с Ь + с.
6) Для любыс натуральныс чисел а, Ь и с справеДлива импликация
(т.е. неравенство а + с < Ь с влечет неравенство а < Ь).
Д о к а з а т е л ь с т в о. Пусть а + с < Ь + с. Тогда b+c = (а с) + и для некоторого числа и . Отсюда очевидным образом следует равенство Ь + с = (а + и) + с .
Применяя теперь закон сокращения, получаем Ь = а + и, откуда а < Ь 
7) Умножение натуральных чисел монотонно, т.е.
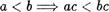
для любых чисел а, Ь, с Е N 
Д о к а з а т е л ь с т в о аналогично доказательству свойства 5.
8) Для любыс натуральныг чисел а, Ь, с и d справеДлива тсажДая из слеДующи.т, Двут импликаций,
(1)
а Ь л с < ас < bd. (2)
Д ок а з а т е л ь с т в о. Докажем сначала (1). Пусть а < Ь
и с < d. Тогда по свойству монотонности сложения получаем а+с b+c и c+b d+b. Отсюда в силу коммутативности сложения и транзитивности отношения < получим, что а + с <
Доказательство импликации (2) можно получить дословным переводом предыдущего текста на ” мультипликативный язык 
Замечание. Свойство 8 часто формулируют в следующем виде: “Неравенства между натуральными числами оДИ7ШКOВ0го смысла можно почленно склаДывать и перемножать 
9) Для любыс натуральныс чисел а и Ь справеДлива кажДая из слеДующис Двус импликаций:
(3)
(4)
Д о к а з а т е л ь с т в о. Покажем справедливость импликации (3). Пусть а < Ь . Тогда Ь = а -4- и для некоторого и е N . При этом возможны случаи:
1 0 ) и = 1 . Тогда Ь а' , т.е. утверждение (З) справедливо; 20 ) и 1 . Тогда по следствию 2 из аксиом Пеано и = v' для некоторого числа 1) и, значит, Ь = а+т,” , откуда в силу свойств 2 и 4 сложения Ь а! + v .
Это означает, что а! < Ь . Таким образом, импликация (З) верна.
Докажем справедливость импликации (4). Пусть а < Ы 
Тогда Ы = а -4- и для некоторого и N 
Возможны случаи: и = 1 либо и 1 .
В случае, если и = 1 , то Ы = а! , откуда в силу аксиомы Р4 имеем Ь = а .
В случае, если и 1 , то, рассуждая так же, как и в случае 20 ) при проверке импликации З), получим Ы = а -4- для некоторого числа v N , откуда ввиду свойства сложения следует Ь —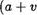 
Далее, применив аксиому Р4 , приходим к равенству Ь = a+ v , откуда а Ь.
Утверждение полностью доказано.
10) Теорема о сравнимости натуральных чисел. Для любыс натуральныс чисел а и Ь справеДливо одно и только одно из соотношений:
1)а 2)a= b; 3)b < а.
Д о к а з а т е л ь с т в о. 1. Докажем справедливость для произвольных чисел а, Ь N хотя бы одного из указанных выше соотношений.
Доказательство инДутсциеб по числу а (при фиксированном Ь N).
Пусть а = 1 . Для числа Ь возможны два случая: Ь — 1 либо Ь 1 .
В первом случае а = Ь , во втором случае 1 < Ь в силу свойства 4, т.е. а < Ь.
Таким образом, при а = 1 и любом числе Ь одно из соотношений, указанных в формулировке теоремы, выполняется.
Предположим теперь, что утверждение справедливо при а = п и произвольном фиксированном числе Ь, т.е. выПОЛняется одно из трех соотношений: п < Ь, либо п = Ь , либо b < n .
Рассмотрим п! и Ь . Если п < Ь , то по свойству 9 справедливо п! < Ь либо Ь . Если п = Ь , то Ь < п! , поскольку п < п! ввиду свойства 3. В случае, если Ь < п, то Ь < в силу свойства З и транзитивности отношения < .
Таким образом, при а = п' хотя бы одно из соотношений 1) — 3) выполняется.
11. Докажем теперь вторую часть теоремы о том, что для любых чисел а и Ь никакие два из соотношений 1) З) не могут выполняться оДновременно.
От противного. Пусть, например, для некоторых чисел а, Ь N выполняются одновременно соотношения 1) и 2), т.е.
Отсюда очевидным образом следует, что а а , что противоречит свойству 1 (антирефлексивности) отношения < .
Аналогично, предположение о справедливости любых двух из трех соотношений 1) — 3) приводит к противоречию. Теорема доказана.
Следствие 1. Умножение уДовлетворяет законам сокращеншя:
Уа, Ь, се N(ac = bc а = Ь), 
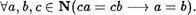
Д о к а з а т е л ь с т в о. Поскольку умножение коммутативно, то достаточно установить справедливость только первой из этих формул. 
Пусть ас — bc для некоторых чисел а, Ь, с ? N . Тогда по теореме о с р ав н и мо с т и н а т ур а л ь н ы х ч и с ел получим для чисел а и Ь возможно одно из следующих трех соотношений:
a < b, b < a, а = Ь.
Из первого неравенства по свойству монотонности умножения вытекает ас < bc , а из второго — bc < ас . Каждое из этих неравенств по теореме о с р а в н и м о с т и н а т у р ал ь н ы х ч и с е л противоречит условию. Следовательно, по той же теореме а Ь .
Следствие 2. Для любыс чисел а, Ь, с тсажДое из неравенств ас < bc либо са < сь влечет а < Ь 
Д о к а з а т е л ь с т в о аналогично доказательству предыдущего следствия.
Замечание. Алгебра является коммутативной полугруппой с еДиницей, уДовлетворяющеб закону сокращеНЕЯ.
Эта полугруппа называется мультипликативной полугруппой натуральных чисел.
11) Отношение ”меньше" во множестве натуральныс чисел удовлетворяет аксиоме Архимеда:
” Для любых натуральных чисел а и Ь найдется число п N такое, что па > Ь. ”
Д о к а з а т е л ь с т в о. Пусть а, Ь N. Тогда а > 1 в силу свойства 4 отношения меньше“ , откуда ab > Ь. Положим п = Ы. Тогда па ап ау = ab + а. Теперь из неравенства ab > Ь следует, что аЬ + а > Ь, т.е. па Ь.
4. Ряд натуральных чисел и его свойства.
Конечные множества
Из свойств 1, 2 и 10 следует, что отношение < является строгим поряДком. Модель , т. е. множество N натуральных чисел с отношением ” меньше“ , называют рядом натуральныс чисел.
Отношение < , определенное по правилу ” а Ь тогда и только тогда, когда а < Ь либо а Ь“, очевидно, будет линебным поряДком на множестве N.
Отношение > , двойственное к < , называется ” больше”
т.е. по определению а > Ь Ь а 
Отметим некоторые очевидные свойства ряда натуральных чисел .
1. ЕДиница является Напл№НЬШИМ элементом ряда натуральныс чисел (следует из свойства 4).
2. В ряду натуральных чисел нет наибольшего (вытекает из свойства 3) 
Понятие наименьшего и наибольшего элементов было дано ранее (59, гл.П).
Другие свойства ряда натуральных чисел будут приведены
ниже.
Непустое поДмножество А множества N называется ограниченным сверху, если
За е NVc е < а).
При этом элемент а называется верснеб границей множества А 
Теорема 1 (о наибольшем натуральном числе). Всякое непустое ограниченное сверсу множество натуральныс чисел соДержит наибольшее число.
(Здесь и далее ради краткости фразы ” множество натуральных чисел“ будет использоваться вместо фразы ” подмножество множества N натуральных чисел“ 
Д о к а з а т е л ь с т в о. Пусть О В С N и В— ограничено сверху. Нужно доказать, что во множестве В есть наибольший элемент.
Доказательство будем вести инДукциеб по версней границе множества В .
ПУСТЬ В ограничено сверху числом 1 (т.е. 1 является одной из верхних границ множества В ). Тогда, поскольку В О 
то очевидно, что В = {1} и, значит, 1 является наибольшим числом в В 
Предположим, что утвержДение теоремы справеДливо Для всякого множества, ограниченного сверсу числом п . Пусть В ограничено сверху числом п! , т.е.
Тогда, если п! ? В , то ту — наибольшее в В число. Если же п! В , то Vz б: п/) : откуда в силу свойства 9 отношения ” меньше“ следует Ус < п) . Это означает, что п является верхней границей множества В .
Следовательно, по индуктивному предположению множество В соДержит наибольший элемент. Теорема доказана.
Теорема 2 (о наименьшем натуральном числе). Всякое непустое множество натуральныс чисел соДержит наименьшее натуральное число.
Д о к а з а т е л ь с т в о. Пусть О А С N. Докажем, что во множе стве А есть наименьшее число.
Если 1 ? А , то 1 — наименьшее число в А . Пусть теперь 1 А . Тогда 1 меньше любого числа из множества А . В этом случае образуем множество
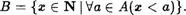
Тогда В О , поскольку 1 ? В 
Кроме того В ограничено сверху любым числом множества А . Следовательно, по предыдущей теореме множество В содержит наибольшее число Ь .
Покажем, что число Ы является наименьшим во множестве А.
Согласно определению множества В получим Уа ? Аф < < а), откуда ввиду свойства 9 отношения меньше“ следует
Уа ? а).
Отсюда легко увидеть, что Ы ? А.
Действительно, если предположить, что Ы А , то высказывание примет вид Уа ? А(Ы < а).
Отсюда по определению множества В вытекает Ы ?- В что в силу Ь < Ы (свойство З отношения меньше“) противоречит выбору числа Ь (оно является наибольшим во множестге В).
Таким образом, Ы ? А, откуда ввиду ( * ) вытекает, что Ы — наименьшее число в А 
Теорема доказана.
Отрезки ряда натуральных.Определение. Пусть п 
фиксированное натуральное число. Множество {с 1 < п} называется отрезком ряда натуральныс чисел с м п и обозначается через 1, п] 
Отрезки ряда натуральных облаДаютп следующими се ойств ахи:
1) Для любого натурального числа п имеет место равенство [1 , па = [1, п] U .
Утверждение является очевидным следствием свойства 9 отношения ” меньше“ 
2) 1, п ? [1, п] Для любого натурального числа п . При этом 1 является НашмеНЬШИМ, а п — наибольшим числом во множестве [1, п] 
Свойство очевидно.
З) Для любыс натуральныс чисел п и т выполняется условие
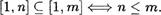
Доказательство предоставляется читателям в качестве упражнения.
4) Для любого натурального числа п отрезок [1, п] является конечным множеством (т.е. не может быть эквивалентен никакой своей правильной части 
Д о к а з а т е л ь с т в о. Применим индукцию по числу п , где п — конец отрезка.
Пусть п = 1. Тогда [1, 1] = 1— одноэлементное множество. Правильной частью его является только пустое множество, которое, очевидно, не может быть эквивалентным одноэлементному множеству.
Предположим теперь, что утверждение справедливо для некоторого фиксированного числа п , т.е. отрезок [1, п] не эквивалентен никакой своей правильной части.
Докажем, что утвержДение справ еДЛИВ0 и Для отрезка [1, па с концом Ж, т.е. что множество [1, па не может быть эквивалентным своей правильной части.
От противного. Пусть
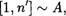(1)
где А— правильная часть множества [1, по, т.е. А С Г 1, п'] и А [1, па.
В силу предположения существует биекция р : [1, 
Очевидно, что множество [1, п] является правильной час 
тью множества [1, п! Это означает, что множество -41 
— п]) также является правильной частью множества А (упр. 1, 512 , гл.П).
Очевидно также, что „41 [1, п] 
Возможны случаи: п' А; п! ? А.
1. Если п' А, то А С [1, п], откуда, поскольку 141 
правильная часть множества А, то и „41 является правильной частью множества [1, п]. Это противоречит индуктивному предположению, поскольку „41 [1, п].
2. Пусть п! ? А. В этом случае положим „42 А 
Тогда 142 — правильная часть множества А (поскольку п] ? ? А) и п' „42, откуда А = „42 U Тогда условие (1) можно записать в виде
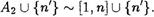
Отсюда, поскольку п! А2 и [1, п], получаем „42 [1, п] (упр. 16, 512, гл.П).
Покажем теперь, что А2 — правильная часть множества
Поскольку т? ? А и А— правильная часть множества [1, пл, то существует элемент т ? [1, по такой, что т А. Отсюда следует, что т п! , поскольку п! ? А и т А. Отсюда ввиду равенства [1, п'] — [1, п] U вытекает, что т ? [1, п]. Поскольку т А, то т „42 и, значит, „42 
правильная часть [1, п]. Таким образом, [1, п] „42 и „42 — правильная часть множества 1, п]. Это противоречит индуктивному предположению.
Следствие. Всякое множество, эквивалентное некоторому отрезку ряда натуральныс чисел; является конечным.
Д о к а з а т е л ь с т в о. Очевидно, что это утверждение является следствием более общего факта:всякое множество, эквивалентное конечному множеству, само конечно.
Докажем последнее утверждение.
Пусть А — конечно и В А, т.е. существует биекция р : В А . Покажем, что В также конечно.
От противного. Предположим, что В эквивалентно некоторой своей правильной части С , т.е. С С В и С В 
Тогда р(С) А и р(С) А) (упр. 1, 12, гл.п), т.е. р(С) — правильная часть множества А . Отсюда р(С) С
(сужение р на множестве С осуществляет эту эквивалентность).
С другой стороны, С В и В А . Применяя свойство транзитивности отношения эквивалентности между множествами (упр. 14, 12, гл.П), получим АС) А, что невозможно, поскольку р(С) — правильная часть множества А и А— конечно,
В действительности можно доказать утверждение, обратное к предыдущему: всякое непустое конечное множество эквивалентно некоторому отрезку ряда натуральныс чисел.
Опустим это доказательство ввиду его громоздкости. Поэтому последнее утверждение можно также принять за определение конечного множества.
5) Отрезки ряда натуральныс чисел с различными концаМи не эквивалентны.
Д о к а з а т е л ь с т в о. Действительно, пусть п т 
Тогда одно из чисел п, т меньше другого.
Пусть, например, п т . Тогда в силу свойства З отрезок [1, п] является правильной частью множества [1, т] , откуда в силу предыдущего свойства 4 вытекает требуемое утверждение .
Дата: 2019-02-02, просмотров: 203.
