Пусть Н — подмножество множества Z целых чисел, определенное равенством

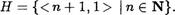
Читатель без труда проверит множество, что Н замкнуто относительно сложения и умножения, т.е. вместе с тсажДыми Двумя своими числами оно соДержит сумму и произееДение. Таким образом, возникает алгебра (Н, -Е, (с носителем Н ) того же типа, что и алгебра натуральных чисел. Зададим отображение ј : N Н по правилу:

ј(п) пф 1, Для любого натурального числа п ? N. Непосредственная проверка показывает, что .i — биекция и

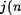                 + т) ј(п) +j(m), j(nm) = ј(п) •j(m).          (5)

Следовательно, алгебра натуральныс чисел изоморфна алгебре (Н, +, Это означает, что Они имеют оДинаковые алгебраические свойства (и отличаются только природой элементов

На этом основании произведем отожДествление: положим 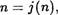 т.е. п  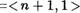Для кажДого п N.

Тогда N С Z. Может возникнуть ” законный“ вопрос: поскольку множество N натуральныс чисел оказалось включенным во множество Z целых чисел, то натуральные числа обязаны Дополнительно уДовлетворять правилам 1, П, III сравнения, сложения и умножения соответственно.

Не приводит ли применение этих правил в каких-либо случаях к противоречию?

Например, если перемножить произвольные натуральные числа п и т по правилу умножения III для целых чисел, то не будет ли это произведение отлично от п • т для некоторых

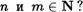
Оказывается, наши сомнения не подтверждаются. Равенства (5) обеспечивают гарантию от таких противоречий.

Действительно, пусть п, т ? N . Перемножим их по правилу умножения целых чисел, т.е. найдем произведение Ј(п) • Ј(т).

Согласно (5), получим ј(п) • j(m) = j(nm)

Таким образом, правила 1, П, III не противоречат соответствующим правилам Для натуральныс чисел.

Отметим некоторые свойства натуральных чисел, вытекающие из правила отожДествления (т.е из соглашения: ј(п) —

п).

Свойство 1. Натуральное число еДиница является еДИНИчет) в кольце целыс чисел.

Действительно, в силу следствия 1 из теоремы 3 следует, что единицей в кольце целых чисел Z служит число е

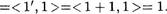
Свойство 2. Для любыс натуральныс п и т справ еДливо равенство п + т, .

Действительно, из условия вытекает <( п + т, т 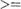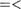п + 1,1 п.

Свойство З. Целое ЧИсЛо < а, Ь > является натуральным тогДа и только тогДа, когДа а > Ь.

Д о к а з а т е л ь с т в о. Пусть а, Ь N. Тогда < а, Ь п + 1, для некоторого п ? N. Отсюда в силу получим а + 1 Ь + п + 1. Это означает, что а Ь.

Теорема 4. Множество Z це,аыс чисел является объеДинением трес множеств, первое Из которыс является множеством N натуральныс чисел, второе — состоит из всес чисел, кажДое из тсоторыс противоположно тс некоторому натуральному числу, и третье — оДноэлементное множество, состоящее из нулевого элемента.

Д о к а з а т е л ь с т в о. Положим N— = {z lz п ? N}. Тогда утверждение теоремы равносильно справедливости следующего равенства:

Z = NUN- И{О}.

Докажем его. Правая часть очевидным образом включается в левую.

Обратно, пусть z — произвольное целое число. Тогда 7- = 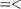а, для некоторых а, Ь ? N.

По теореме о с р ав н и мо сти н ат ур аль н ы х ч и с ел для ab выполняется одно и только одно из условий а = Ь, а >

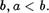
В первом случае z а, 0, во втором— z е N по свойству 3 и в третьем z а, Ь поскольку 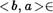 N.

Теорема 5. КажДое целое число а, Ь > является разностью Деус натуральныс чисел, а именно: Ь а — Ь.

Д о к а з а т е л ь с т в о. Нужно доказать, что а, +b = а. Подсчитаем левую часть этого равенства:

2. Упорядоченность кольца целых чисел. Теоремы о