В дальнейшем будем говорить, что множество А содержит п элементов или мощность множества А равна п , если А эквивалентно отрезку [1, п] ряда натуральныс чисел с концом п .

Мощность множества А обозначается символом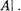

Теорема 1. Пусть А — конечное множество, и п. ТогДа множество „41 , полученное из А присоеДинением одного элемента (т.е. г: А U {b} и Ь А), — конечно и

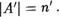
Д о к а з а т е л ь с т в о. Пусть А ре [1, п] и 24' = АИ{Ь} где Ь А . Тогда, существует биекция р : А [1, п] .

    Построим отображение ф : А!   [1, по по правилу:

ф(а) р(а) для любого а ? А и ф(Ь) . Легко проверить, что ф — биекция.

Отсюда следует, что „4' [1, па .

Теорема 2. Объединение Двус конечныс множеств А и В — конечное множество. При этом если множества А и В не пересекаются, т.е. А ПВ = О, то 1 А U Bl = lAl + [В! .

       Д о к а з а т е л ь с т в о. Пусть 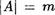 и             = п,

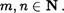
1. Докажем, что множество А U В — конечно. Зафиксируем произвольное число т и проведем доказательство индукцией по числу п .

Пусть = 1 , т.е. В = {b} . Тогда, если Ь ? А, то AUB — А, и если Ь А, то А ИВ = „4' .

В первом случае А И В — конечно в силу конечности множества, и во втором случае утверждение следует из теоремы 1. Допустим теперь, что утверждение справедливо для всех множеств В, мощность которых равна п .

Тогда, по определению, всякое множество, содержащее элементов будет эквивалентным множеству [1, п!

U{n'} . Полагая В [1, п], получим А U В! (А И U{n'} . Правая часть полученного равенства равна либо А С) В либо (А U Ву , откуда в силу индуктивного предположения (и теоремы 1 во втором случае) получим требуемое утверждение.

2. Пусть А П В = О . Доказательство так же, как и в п. 1, проводится индукцией, по мощности множества В (при фиксированном множестве А ).

Теорема З. Декартово произвеДение Двус конечныс множесте — конечно. При этом если = т и lBl = п, то

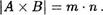
Доказательство предоставляется читателю в качестве упражнения. Скажем лишь, что его легко получить, если использовать индукцию по мощности множества В

5. Вторая и третья формы метода

Математической индукции

Теорема 1 (вторая форма метода математической индукции). Пусть Р(с) — некоторый оДноместныб преДикат, опреДеленный на множестве натуральныс чисел. ТогДа если предложение Р(г) справеДливо Для некоторого натурального числа К и Для произвольного натурального числа п К из справеДливости преДложения Р(с) Для всес натуральныс чисел с , уДовлетпворяющис неравенству К < с < п, слеДует справалив ость этого преДложения Для числа п , то это преДложение справеДлиео Для всес чисел с > К

Д о к а з а т е л ь с т в о. Пусть выполнены все условия теоремы, т.е. для некоторого числа К высказывание Р (К) истинно и для произвольного фиксированного числа п К из формулы Ус(К < с < следует Р (п) . Нужно доказать, что утверждение Р(с) верно для всех с > К .

От противного. Допустим, что существует т > К такое, что Р(т) — ложно. Тогда т > К , поскольку по условию Р(К) —

истинно.

Образуем множество М {с > К Р (с) — ложно }. Тогда М О, так как т М .

В силу теоремы о н а и м е н ь ш е м н а т у р а л ь н о м ч и с л е множество М содержит наименьшее число п .

  Отсюда п > К , Р(п) — ложно и ? М (п < с) .

Покажем, что высказывание Vc(k < с < n)P(z) истинно. Заметим, что Р(г) не может быть ложными ни Для какого числа с, уДовлетворяющего неравенству К < аз < п .

Действительно, если предположить, что Р (Ь) ложно для какого-нибудь числа Ь такого, что К < Ь п, то Ь ? М по определению множества М . Но это невозможно в виду того, что Ь п и п— наименьшее число во множестве М.

Таким образом, Ус(К < с < п)Р(с)— истинно, откуда по условию следует, что Р(п) — истинно. Но ранее отмечалось, что Р (п) — ложно. Получено противоречие. Теорема доказана.

Замечание. На практике теорема 1 иногда используется в следующей формулировке: ” Для того, чтобы доказать утверждение Р(с) для всех натуральных чисел с > К, где К — некоторое фиксированное натуральное число, достаточно выполнить два шага:

1-й шаг — установить, что Р (К) истинно;

2-й шаг — для произвольного фиксированного числа п > К проверить справедливость импликации

Vz(k < с < 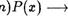 Р(п')

(для чего, в свою очередь, достаточно предположить, что Р(с) истинно для всех чисел с таких, что К < с < п, и доказать истинность Р (Ы) ) ”

Последовательность, состоящая из этих двух шагов, называется метоДом математической инДукции во второй форме.

Теорема 2 (третья форма метода математической индукции). Пусть Р (с) — оДноместньиј преДитсат, опреДеленный на множестве ТЧ натуральныс чисел. Тогда, если преДложение Р(с) истинно Для всес чисел некоторого бесконечного подмножества М множества N натуральныс чисел и Для произвольного натурального числа п из истинности Р(п') слеДует истинность Р(п) , то Р(с) истинно Для всес натуральныс чисел.

Д о к а з а т е л ь с т в о. Пусть выполнены все условия теоремы:

1) Существует бесконечное поДмножество М множества N натуральныс чисел, такое что преДложение Р (с) истинно Для всес чисел из М 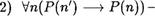истинно.

Нужно доказать, что Р(с) верно Для всес натуральныс чисел.

От противного. Допустим, что утверждение теоремы не верно, т.е. Р(а) — ложно Для некоторого числа а N

Поскольку отрезок [1, п] является конечным множеством, а множество М бесконечно, то найдется число Ь ? М такое, что    [1, п], т.е.   Ь.

Образуем множество А = {с с Ь и Р(с) — ложно 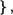тогда а ? А и, следовательно, А О

По определению множество А ограничено сверху числом Ь , откуда по теореме о н аи б о л ь ш ем н ат у р ал ь н о м ч и с л е множество содержит наибольшее натуральное число с. Тогда с Ь, Р(с) — ложно и Ус А(с < с)

Докажем, что Р (8) — истинно. Из неравенства с Ь в силу свойства 9 отношения ” меньше“ следует, что 8 < Ь . Действительно, если Ь , то Р(8) — истинно, поскольку Ь ? М Если с' < Ь , то Р(с') не может быть ложным, так как в этом случае с! ? А , а число с наибольшее в А.

Таким образом, Р (8) — истинно, откуда по условию Р(с) — истинно, что противоречит принадлежности с ? А . Теорема доказана.

У пр аж н е н и я:

1. Докажите теорему существования и единственности умножения натуральных чисел ( 2, гл.Ш).

2. Докажите:

(а) свойство 7 неравенств между натуральными числами ( 5 З, гл.Ш);

(Ь) импликацию (2) в свойстве 8 ( З, гл.Ш);

(с) следствие 2 ( 5 З, гл.Ш);

(d) импликации [1, п] С [1, т] л т п < т;

(е) равенство [1, п']

3. Завершите доказательство теоремы 2 о к о н е ч н ы х м н о ж е с т в ах ( 54, гл.Ш).

4. Докажите теорему З о к о н е ч н ы х м н о ж е с т в ах ( 54, гл.Ш).

Гл ав а IV