Пусть а и Ь— натуральные числа и а Ь . Тогда по определению а = Ь + и для некоторого и ? N . Число и в этом случае называется разностью чИ(хЛ а и Ь и обозначается через а — Ь , т.е. в виде равенства и = а — Ь .
Таким образом, во множестве натуральных чисел разность между двумя числами а и Ь существует не есегДа, а только тогДа, когДа уменьшаемое число а больше вычитаемого — Ь.
Ниже мы построим кольцо Z целых чисел, которое включает в себя алгебру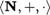 
и лишено этого ” дефекта“ .
Отметим для этого некоторые основополагающие свойства разностей натуральных чисел.
Теорема 1. Разности натуральныс чисел (в случае, если они существуют) облаДают слеДующими свойствами:
Для любыс чисел а, Ь, с, d e N , где а и с > d.
Д о к а з а т е л ь с т в о. Пусть а > Ь и с > d. Положим а — Ь = и и с — ю. Тогда а = Ь + и и c = d + v. (1)
1. Пусть а — Ь с — d, т.е. и = v . Складывая почленно равенства (1) (предварительно заменив одно из них симметричным) и применяя свойства сложения (ассоциативность, коммутативность), получим
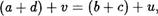(2)
откуда, поскольку и = 1) , по закону сокращения для сложения натуральных чисел следует а + d = Ь + с .
Этим доказана импликация а — Ь = с — d а d = Ь + с .
Обратно, если а + d Ь -4- с, то, применяя снова закон сокращения к равенству (2), получим, что и = , т.е. а — Ь 
— c— d.
2. Из (1), очевидно, следует, что а + с (Ь + d) + (и + v) 
откуда u+v (а л- с) — (Ь + d) , т.е. (а — Ь) + (c—d) (а 4- с) 
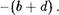
З. Перемножая почленно равенство (1) и применяя свойства дистрибутивности умножения относительно сложения (и также свойства сложения), получим
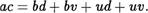
Прибавляя к обеим частям этого равенства число bd , приходим к равенству ас + bd = 2bd + bv + ud + ит —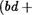 
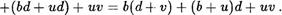
(Читатель, по нашему мнению, уже хорошо владеет своиствами операций сложения и умножения натуральных чисел, поэтому в дальнейшем мы иногда будем опускать ссылкй на них.
Из последней цепочки равенств в силу (1) следует ac+bd — 
Ьс + ad + uv , откуда uv = (ас + bd) — (dc + ad), и, значит, равенство (1) справедливо.
Теорема доказана.
Заметим, что если разность а — Ь чисел а и Ь обозначить в виде упорядоченной пары натуральных чисел (а, Ь), то условия 1 — З теоремы 1 автоматически запишутся в виде:
1'.
2'.
3'. (а, Ь) • (с, d) = (ас + bd, ad + Ьс) .
Однако при этом мы сразу обнаруживаем, что отношение ” равенства” , заданное на множестве N х N в действительности не является равенством, поскольку по правилу 1' различные элементы этого множества оказались равными (например,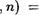 
(Ы, п!) для любого п ? N). А ”операции -Е, • ”, в действительности не являются операциями (они не обладают свойством однозначности) 
Эту ” небрежность“ можно легко исправить, если знак равенства в 1' заменить знаком некоторого бинарного отношения р на множестве N х N и в дальнейшем внести коррективы в
Определение. Пусть (а, Ь), (с, d) е N х N . Полагаем (по определению)
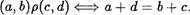(3)
Следствие 1. Отношение р является эквивалентностью на множестве N х N 
Предоставляем читателю возможность доказать это следствие самостоятельно.
Далее через (а, Ь) обозначим класс эквивалентности р с порожДающим элементом (а, Ь) . Символ р заменим в дальнейшем на стандартный знак . Напомним, что по определению
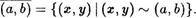
Из свойств эквивалентности следует
откуда в силу (З) получим:
Таким образом, условие 1' можно заменить корректным условием I равенства классов эквивалентности 
Тогда условия 2' и 3', естественно, заменяются следующими:
(а + с, Ь + d) (правило сложения);
(ас + bd, ad + bc) (правило умножения).
Поскольку каждый класс эквивалентности определяется любым своим элементом, т.е. каждый класс записывается неоднозначно (это видно, например, из условия 1), то естественно возникает вопрос, не изменяются ли результаты сложения и умножения классов эквивалентности при выборе в них других представителеи?
Другими словами, определяет ли каждое из правил П и III соответственно алгебраическую операцию?
Положительный ответ на этот вопрос, например, для сложения должен означать, что сумма не изменяется при замене слагаемыс равными им элементами. Это свойство называется свойством оДнозначности операции.
Теорема 2. Правила П и III опреДеляют алгебраическую операцию (на множестве классов эквивалентности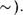 
Д о к а з а т е л ь с т в о. Проверим, например, что умножение однозначно, т.е. если в произведении (а, Ь) • (К, l) сомножители заменить равными, то результат не изменится.
1. Чтобы облегчить вычисление, покажем сначала, что если в произвеДении заменить только один сомножитель равным ему, то результат не изменится, т.е. если (а, Ь) (с, ф, то ба, Ь) • (К, l) —
Докажем, например, импликацию
(с, d) (а, Ь) (КД) = (с, ф • (К, l).
Пусть (а, Ь) — (с, d) . Тогда a+d = Ь+с . Покажем (а, l) = — (с, l), т.е. (ак 4- Ы, al А- bk) — (ск + Ш, cl -4- dk). Последнее равенство равносильно следующему:
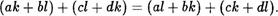(4)
Установим его справедливость.
Заметим, что после простых преобразований левая часть последнего условного ” равенства“ (истинность которого надо установить) становится равной (а + d)k + (Ь + , и правая — (а + + (Ь + .
По условию а + d Ь + с, откуда очевидным образом вытекают следующие два равенства (а +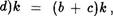 
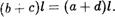
Складывая их почленно, приходим к равенству, левая часть которого равна левой части, а правая — правой части равенст-
Таким образом, равенство (4) — верно.
Аналогично доказывается, что произвеДение не изменится, если второб сомножитель заменить равным ему.
2. Теперь перейдем к общему случаю. Пусть (а, Ь) —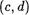 
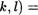(9, f). Тогда, согласно пункту 1, справедливы равенства (а, l) = (с, ф • (К, l) и (с, d)• (К, l) = (с, d)• (9, f) , откуда по транзитивности получим, что (а, Ь) • (К, l) —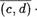 
Аналогично доказывается однозначность сложения.
Теорема доказана.
Обозначим через Z фактор-множество N х N/r•u (см. 10, гл.П) по отношению , т.е. Z состоит из всех классов эквивалентности , определенной на множестве N х N по правилу (З).
Определение. Алгебра (Z, + , с носителем Z и операчиямИ сложения ” + ” и умножения , опреДеленными по правилам П и соответственно, называется алгеброй целыс чисел. При этом кажДый элемент множества Z назыеается целым ЧИсЛОМ.
В дальнейшем примем более экономные обозначения: целое число (а, Ь) будем обозначать через а, > . Тогда правила 1, П, III примут вид:
.
Теорема З. Целые числа относительно сложения и умножеНИЯ образуют коммутативное кольцо с еДиниией.
Д о к а з а т е л ь с т в о. Покажем, что целые числа относительно сложения образуют абелеву группу.
Ассоциативность и коммутативность сложения целых чисел очевидным образом вытекают из определения П операции сложения и соответствующих свойств сложения натуральных чисел .
Далее, пусть < а, — произвольное целое число.
Тогда Ка, + 1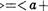 
1, b+ 1 а, поскольку
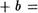(Ь -4- 1) + а (что обеспечивает ввиду правила 
последнее равенство 
Таким образом,
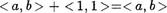
для любого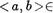 
Z.
Следовательно, целое число < 1, 1 > является нулём в алгебре -Ю. Будем обозначать это число в дальнейшем стандартным символом О.
Отметим, что 0 п, п > для любого натурального числа п, поскольку < п, 1, в силу правила 1.
Проверим последнюю аксиому сложения. Очевидно, что
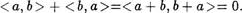
Это означает, что число < Ь, а > является противоположным к <a,b>, то есть 
Окончательно имеем, что (Z, -Ю — абелева группа.
Проверим аксиомы умножения.
Ассоциативность. Пусть < а, Ь < с, d < КД Z, нужно доказать равенство
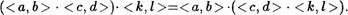
Чтобы убедиться в справедливости этого равенства, достаточно вычислить левую и правую его части, а затем сравнить результаты, пользуясь правилом 1. Никаких искусственных препятствий на этом пути не возникает. Поэтому предлагаем читателю завершить доказательство.
Аналогичным образом доказываются коммутативность умножения и Дистрибутивность умножения относительно сложения.
Таким образом, алгебра (Z, -Ю является коммутативным
КОЛЬЦОМ.
Покажем, что это кольцо имеет единицу.
Положим е 1', 1> и докажем, что z • е = z для любого z e z.
Действительно, пусть z а, b>, а, Ь N 
Тогда ze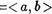 
• <1 f , 
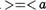• 1' + Ь • 
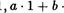1 Ъ.
Покажем, что последнее число в этой цепочке равно < а, Ь >. Для этого ввиду правила достаточно доказать равенство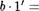 
Ь + а • 1' + Ь, но оно очевидным образом вытекает из свойств операции сложения и умножения над натуральными числами .
Таким образом, элемент е 1', 1 > является единицей в кольце целых Z чисел.
Следствие 1. Для любого натурального числа п целое число п, п > является нулем, а — < Ж, п — еДиницей в кольце Z целыс чисел.
Следствие 2. Для любого целого ЧИсЛо < а, справеДливо равенство —<а,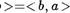 
.
Действительно, поскольку
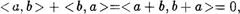
то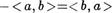 
.
Определение. Пусть К — произвольное ненулевое коммутативное кольцо с еДиницеб е. ТогДа элемент а ? К, отличный от нуля, называется Делителем нуля, если Для него найДется также ненулевой элемент Ь (- К такой, что ab = 0.
Легко показать, что любое поле не соДержит Делителей нуля.
Действительно, пусть К — поле и ab О для некоторых а, Ь ? К. Тогда, если а 0, то элемент имеет обратный а—1 
Умножая почленно равенство ab = 0 на а приходим к равенству Ь — 0, т.е. при а О и Ь 0 равенство ab — 
невозможно.
Следствие З. Кольцо Z целыс чисел не имеет Делителей нуля.
Предлагаем читателю доказать утверждение в качестве упражнения.
Следствие 4. В кольче Z целыс чисел справеДлива иммикация ас = bc Л с + 0 а = Ь
Для любыс а. Ь, се Z.
Доказательство очевидным образом вытекает из следствия З.
Дата: 2019-02-02, просмотров: 275.
