Множество 01 U 02 , состоящее из сИМВоЛов операциб Fi(i = 1, . К) и отношений Рј(ј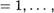 
s), называют-п сигнатурой системы. При этом называют функциональной, а 02 — преДикатпной частью сигнатуры Данной системы.
Сигнатура алгебраической системы может быть и бесконечнотЈ (условие конечности в приведенном выше определении выбрано ради краткости) 
Алгебраическая система — это множество (носитель) с набором (возможно бесконечным) операций и отношений, определенных на этом множестве.
Алгебраическая система называется алгеброй, если преДикатная часть ее сигнатуры является пустым множеством (02 О). 
Если же функциональная часть сигнатуры алгебраическоб системы пуста, т. е. 01 = 0, то эта система называетпся моДелью.
Отметим, что создателем теории алгебраических систем является выдающийся советский математик А. И. Мальцев (1909 — 1967). Читатель, желающий познакомиться с основными идеями этой теории, может обратиться к книге [10]. П р им е р ы:
Пусть символы F1 и F2 обозначают, соответственно, операции сложения и умножения на множестве N натуральных чисел, а Р— отношение < меньше либо равно“ ) 
Тогда следующие три алгебраические системы
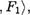(N,F2), 
являются алгебрами. Первые две из них имеют тип (2) , а тип третьей равен (2, .
Алгебраическая система (N, Р) является моДелью.
Алгебраическая система F1, Р) имеет тип (2; 2) . Она не является ни алгеброй, ни моДелью.
Другие примеры будут приведены ниже.
Классические алгебры
1. Алгебра с оДнотј бинарной операцией называется группоидом.
Например, каждое из множеств N, Z, Q,R образует группоив относительно операции сложения либо умножения.
2. Алгебра с оДной бинарной ассоциативной операцией называется полугруппой.
Очевидно, все группоиды, указанные в предыдущем пункте, являются полугруппами. Однако в общем случае это утверждение не верно, т.е. масс группоиДов более ШИРОК, чем класс полугрупп.
Например, целые числа относительно операции вычитаНИЯ образуют неассоциатпивныб группоиД.
Приведем другой пример группоида, который не является полугруппой.
Пусть А = {а, b} — двухэлементное множество. Зададим операцию Т на множестве А следующими равенствами:
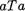= Ь, аТЬ = а, ЬТа= Ь, ЬТЬ= а.
Тогда (аТЬ)Та = ата Ь . В то же время аТ(ЬТа) = аТЬ = а, и, значит, (аТЬ)Та аТ(ЬТа) .
Следовательно, операция Т неассоциативна. Это означает, что группоид (А, Т) не является полугруппой.
Заметим, что операции Т , построенной в предыдущем примере, соответствует следующая таблица:
Такие таблицы называются таблицами Кэли. Они используются, как правило, для задания бинарной операции на конечном множестве и устроены следующим образом.
Элементы носителя А записывают в верхней строке и в левом вертикальном столбце. Далее для каждой упорядоченной пары (с, у) „42 результат (СТу) помещается е клетку, стоящую на пересечении строки, соДержащетј элемент с, и столбца, соДержащего элемент у.
В теории полугрупп важнейшую роль играют так называемые полугруппы отображений множеств (в себя)“ 
Устроены они так: 
Пусть А— произвольное фиксированное множество. В качестве носителя полугруппы выбирается множество М (А) 
состоящее из всех отображений множества А в себя:
М (А) = {f f : А А — отображение } 
Операцией на множестве М (А) служит КомпоЗицИЯ отображений (гл.П, 5).
Очевидно, что для любых f,g е М(А) их композиция 9 о f также является отображением множества А в себя и, следовательно, g о f М (А) . Ассоциативность операции о компоЗИЦИИ гарантируется теоремой 1 (гл.П, 5).
Таким образом; (М (А), о) — полугруппа для любого множества А .
З. Полугруппа (G, Т) называется группой, если она И.,иеет нейтральный элемент, относительно которого любой элемент а Е- имеет симметричный элемент.
Позже будет показано, что это определение избыточно“ ,
т.е. можно некоторые требования в определении ослабить.
С этой целью сформулируем определение группы в мультиплитсатпивнотј терминологии.
ГруппоиД • ) с операцией умножения называется группой, если выполнены слеДующие условия:
1. ма, Ь, с ? ((ab)c = a(bc)) ассоциативность операции умножения 
(элемент е называют при этом правоб еДиницеб);
З. е G-3b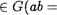 
е)
элемент Ь называется правым обратным для а 
Условия 1 — З называют аксиомами группы. Опираясь на них, можно доказать, что в группе существует только одна еДинича е , которая является оДновременно и правой, и левот). Нитсагстс Другис еДиниц ни правых, ни левыс не существ ует.
Аналогичное утверждение имеет место и Для элемента, обратного к любому Данному. В связи с этим элемент, обратный к элементу а, имеет стандартное обозначение а—1 
Таким образом, последнее определение группы равносильно исходному, но оно содержит ” меньше“ требований (требуется наличие только правой еДиницы, и для каждого элемента 
существование только правого обратного) 
Для перевода определения группы на аДДитпивньи) язык достаточно: знак умножения (0 заменить знаком сложения (+) слова ” произведение” , ” единица“ и ” обратный“ , соответственно, — словами ” сумма“ , ” нуль“ и ” противоположныи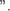 
Аксиомы 1 — З будут выглядеть так:
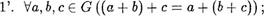
2'. ЗО ? GVa 
3'. G3b е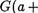 
Элемент, противоположный элементу а, обозначается через (—а).
Группа (G, Т) называется коммутативной, либо абелевой, если групповая операция Т коммутатив на, т. е.
Уа, Ь е G(aTb = ьта).
Для абелевыс групп, как правило, используется аДДитивная терминология.
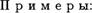
Каждое из множеств Z, Q и R образует группу относи 
тельно операции сложения.
Однако, натуральные числа не образуют ни по сложению, ни по умножению.
Очевидно также, что если в качестве носителя выбрать одно из множеств 
Q+, R+ , где Q+, R+ обозначают множества положительных рациональных и действительНЫХ чисел, соответственно, то получим группу относительно умножения.
Важнейший класс в теории групп образуют так называемые “группы преобразований“ или ”группы поДстановок 
Преобразованием множества А называется любое биекпивное отображение множества А на себя.
Зафиксируем множество А, и через S(A) обозначим множество всес биекций f : А А 
S(A) = {fl f : А А — биекция }.
Тогда нетрудно показать, что композиция любых двух отображений из S(A) снова является биекцией (см., напр., упр. 12, с. 47) и, следовательно, .q о f ? S(A) . Таким образом, композиция является бинарной операцией на множестве S(A) . Теперь уже легко установить, что алгебра о) является группой.
Действительно, ассоциативность операции вытекает из теоремы 1 (гл.П, 5). В этой же теореме содержится утверждение о том, что тождественное отображение 1 А множества А играет роль еДиницы при композиции отображений. Следовательно, композиция удовлетворяет аксиомам 1 и 2.
Проверим выполнимость третьей аксиомы. Пусть f Е? S(A) , тогда f : А А— биекция.
Тогда по признаку обратимости отображения существует отображение f—1 : А А, обратное к f, т.е. f o f 1 
—1 -1
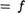о f 1 А. Это означает, что f — обратимо. Отсюда снова по той же теореме 2 получим, что f—1 — биекция и, следовательно, ? S(A) 
Таким образом, и третья аксиома выполняется и, значит,
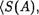о) — группа.
Если А— конечное множество, то вместо термина ” преобразование“ используется его синоним “поДстановка 
В этом случае, если множество А содержит п элементов, то вместо S(A) используется запись Sn 
Группа Sn называется группой поДстановок п -й степени или симметрической группой п -6 степени. Нетрудно проверить, что она содержит п! элементов.
Пусть (G, Т) и (L, — группоиды.
Определение. ГруппоиД (G, Т) назыв ается изоморфным группоиДу /\L, , если существует боекциЯ р : G L такая, что
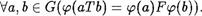
Биекцию р 6 этом случае назыв ают отображением, осуществляющим изоморфизм Данных группоиДов.
Заметим, что условие (*) в словесной формулировке часто выражают словами: “отображение р сосраняет групповую операцию Т 
Из определения очевидным образом следует, что отношеНИе изоморфизма межау группами облаДает свобствами рефлексивности, симметричности и транзитивности.
Запись G .L означает, что группоид Т) изоморфен группоиду (L, Р) .
Нетрудно проверить, что в этом случае, если Т) является группой, то и /\L, Р) — также группа.
П р и м е р ы:
1. Пусть G Z и Т— сложение. Ранее уже отмечалось, что 4) — группа.
Пусть L = {z | z ? Z,z — 2k К ? Z и 17 — умножение (на множестве L ).
Легко проверить, что Е) — группа.
Пусть f : Z L— отображение, определяемое по правилу:
ЛК) 2k для любого К ? Z 
Покажем, что f осуществляет изоморфизм Z .
Действительно, если К2 , то одно из этих чисел меньше другого. Пусть, например, К2 . Тогда, поскольку f— возрастающая функция, то f(k1) < f(k2) , т.е.
f(k2).
Следовательно, инъективно. Сюръективность отображения f очевидна, и, значит, f — биекция.
Проверим теперь, что отображение f удовлетворяет услоВИЮ ( * 
Пусть К1, К2 ? Z. Тогда f(k1 + К2) — 2k1 +k2 2k1 • 2k2 
= f(k1) • f(k2) . Утверждение доказано.
2. R+ — множество положительных действительных чисел. Тогда, как уже отмечалось, ( R+ , является группой относительно операции умножения.
Нетрудно проверить, что отображение р : R R , опреДеленное по правилу р(а) lna для любого а ? R+ , осуществляет изоморфизм межау группой (R + , и аДДитпивно1ј группой -Е, •
Действительно, биективность р очевиДна, а условие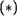 
выполняется в силу равенства ln(ab) — ln а + ln Ь для любых а, Ь е R+ (т.е. p(ab) р(а) + p(b) ).
Понятие изоморфизма играет фунДаментальную роль в математике. Из определения следует непосредственно, что изоморфные группоиДы имеют одинаковое количество элементов. Читатель без особого труда докажет, что “еДиница группы при изоморфизме пересоДит (отображается) в еДиницу Другоб группы, элемент, обратный тс Данному, — в обратный 
его образу“ и т.д. Несколько больших усилий требуется для понимания и доказательства следующего (более общего) утверждения: ”Если некоторая формула ИСЧИСЛеНИЯ преДикатов истинна на оДной из изоморфныс межДу собой группас, то она истинна и на Другой ”.
Другими словами, изоморфные группы имеют оДинаковые алгебраические свойства (т.е. свойства, сформулированные в общелогических терминах и терминах операций, с помощью которых заданы данные группы) 
Это замечание справедливо и для любых алгебр, изоморфных между собой. Однако понятие изоморфизма для произвольных алгебр нами еще не дано. Приведем его.
Заметим, что если результат бинарной операции Т над элементами а1 и а2 записывать через т (щ , (12), то условие 
примет вид: 
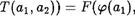р(а2)).
В этом виде оно легко обобщается на любую п -арную операцию. А именно, пусть (G, Т) и ф, — оанотипные алгебры с одной п -арной операцией Т, F, соответственно. Тогда биекпивное отображение р : G L называется изоморфизмом, если выполняется условие
В этом случае также говорят, что отображение р сосраняет операцию Т.
Определение. Пусть (G, Т! , тк) и F1, . . .Fk>— одНОТИПНЫе алгебры. Тогда биекциЯ р : 6' L называется изоморфизмом, если она сосраняет кажДую из операций
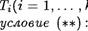К) , т.е. для каждого i ? {1, К} выполняется
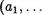,ant)) = 
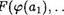. , р(ап;))
для любых (11, . ати ( есть арность операции 1'i ) 
Пусть Т) — некоторая группа и S — непустое подмножество в G , замкнутое относительно операции Т , т.е.
Уа, Ь ? S(aTb ? S).
Тогда очевидно, что (S, Т) является группоиДом. Группо 
ид (S, Т) называется поДгруппоб группы Т) , если он сам является группой, т.е. на множестве S выполняются аксиомы 1 — З.
Следующая теорема указывает на особую роль групп подстановок в общей теории групп.
Теорема Кэли. Любая конечная группа изоморфна некоторой поДгруппе группы Sn поДстановок (действующих на носителе этой группы 
Таким образом, при исследовании свойств конечных групп достаточно ограничиться классом всех подгрупп групп подстановок.
Заметим, что современная теория групп своим зарождением и дальнейшим развитием обязана группам- подстановок.
Понятие группы было введено в 1830г. французским математиком Эваристом Галуа, который успешно использовал понятие группы подстановок для решения знаменитой проблемы об условияс разрешимости алгебраическис уравнений в радитсалас.
4. Алгебра (К, -е, •У с Двумя бИНЧНЫМИ операциями — сложением U умножением — называется кольцом, если выполнены следующие условия (аксиомы кольца):
1) Относительно сложения элементы множества К образуют абелеву группу, т. е. алгебра (К, -Е, — абелева группа.
2) Умножение ассоциативно в К , т.е. алгебра (К, является полугруппой.
З) Умножение Дистрибутивно относительно сложения,
т.е. выполняются слеДующие тожДестеа:
Уа, Ь, с ? К ( (а + = ас + Ьс),
Уа, Ь, с ? + Ь) = сан- cb).
Группа (К, -Е) при этом называется аДДитивной группой, а полугруппа КК, » - мультипликативной полугруппойкольца К 
Заметим, что первая аксиома является конъюнкцией аксиом, входящих в определение абелевой группы.
П р и м ер ы:
Целые числа относительно сложения и умножения образуют кольцо р, -е, » •
Если в этом предложении заменить Z на любое из множеств Q или R , то также получим кольцо.
Читатель, знакомый с арифметикой матриц, без труда поймет, что если основное множество К (носитель) некоторого кольца (К, + , заменить множеством всес кваДратныс матриц фиксированного порядка с элементами из К , то снова получим кольцо.
Легко проверяется, что множество четныс целыс чисел также является кольцом.
Однако натуральные числа кольца не образуют, (N, не является группой.
Если умножение в кольце К коммутативно, т.е. ab = ба для любых элементов а, Ь е К , то кольцо К называется коммутатиеным.
Например, все кольца с числовыми элементами коммутативны. Но кольца, элементами которых служат матрицы, могут не обладать таким свойством. Например, кольцо всес матриц с целыми элементами не является коммутативным.
Если мультипликативная полугруппа кольца К содержит еДиницу, т.е. такой элемент е , что ае — еа = а для любого элемента а ? К , то этот элемент е называется единичей кольца К , а само кольцо К — кольцом с еДиницеб.
Например, кольцо Z целых чисел, а также кольцо всех квадратных матриц фиксированного порядка с элементами из Z имеет единицу. Напротив, кольцо четныс целых чисел является кольцом без еДиницы.
Из определения кольца непосредственно вытекают следующие свойства:
1. Уа, Ь, — = ас — bc].
са — cb]
т. е. умножение дистрибутивно относительно вычитания).
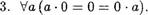
4. Если кольцо К с еДиницей е соДержит более одного элемента, то е О 
Действительно, если допустить, что е 0 , то для любого элемента а ? К получим а а е = а • О = О. т.е. К = {О} 
Противоречие с условием.
Всякое кольцо, содержащее более одного элемента, называется ненулевым.
Пусть К — ненулевое коммутативное кольцо с единицей е . Элемент а ? К называют обратимым, если существует элемент элемента Ь ? К такой, что ab = ба = е. При этом элемент Ь называют обратным к а . Нетрудно установить, что если элемент, обратный тс а, существует, то он еДинственен (см. доказательство следствия из теоремы 2, 5, гл.П).
Поэтому элемент, обратный к а, имеет стандартное обо-
значение а—1 
Приложив небольшие усилия, читатель может доказать, что обратимые элементы кольца образуют группу относителВно умножения. Эта группа называется мультипликативной группой Данного кольца. Например, мультипликативная группа кольца Z целых чисел состоит из чисел 1 и —1.
Ненулевое коммутативное кольцо Р с еДиницей называется полем, если кажДыб его отличный от нуля элемент об-
ратим.
Например, каждое из колец Q и R , рациональныс и Действ ительныс чисел, соответственно, является полем. Напротив, кольцо Z целыс чисел полем не является.
Заметим, что в любом поле Р мультипликативная группа состоит иЗ всес ненулевыс элементов.
У п р аж н е н и я:
1. Пусть р : А В— биекция и С— правильная часть множества А (см. с. 16). Докажите, что р(С) — правильная часть множества В .
2. Какие из отношений, определенных ниже, рефлексивны, симметричны, антисимметричны, являются отношением частичного порядка, либо эквивалентностью?
(а) отношение параллельности (перпендикулярности) на
множестве прямых плоскости;
(Ь) отношение подобия треугольников;
(с) отношение коллинеарности векторов;
(d) отношение R на множестве Z целых чисел, определенное по правилу (а, Ь) е R (а — Ь)/5 е Z;
(е) отношение ” включения“ на множестве всех подмножеств некоторого универсального множества.
З. Будет ли отношение делимости, т.е. отношение, определенное по правилу (а, Ь) ? R а делитель Ь, отношением частичного порядка:
(а) на множестве N натуральных чисел? (Ь) на множестве Z целых чисел?
4. Сколько различных бинарных отношений существует на множестве, состоящем из п элементов?
5. Докажите, что всякое антирефлексивное и транзитивное ОТНОШение (т.е. отношение строгого порядка) является антисимметричным. 6. Докажите предложение, сформулированное на с. 54 
7. Докажите равенства
С -1 ) -1 (F0S) -l = S -1 —1 для любых бинарных отношений F и S.
8. Докажите, что для любых отношений F и S, определенных на данном множестве А, справедливы следующие свойства:
(а) (Fu S) -1 U s -1 ф) (Fn S) -1 Р-1 ns -1
(d) FC S Р -1 С S -1
9. Пусть F,S, F1, S1 — бинарные отношения, определенные на множестве А . Докажите, что
— F 0S C F1 0Sl.
10. Пусть — произвольное бинарное отношение на множестве А . Докажите, что отношения FnF—1 и FUF —1 симметричны.
11. Пусть {Xi 'i ? I} — разбиение некоторого множества Х. Доказать, что отношение R на множестве Х, определенное по правилу
(с,у) 
3i e 
ХО,
является эквивалентностью и найти классы этой эквивалентности.
12. Пусть Е — бинарное отношение на множестве А. Докажите, что F является эквивалентностью тогда и только тогда, когда выполняются оДновременно следующие условия:
(а) Д С F , где Д — диагональ множества А ,
ф) F-i = F•
(с) (F0F= F.
13. Докажите, что ядро любого отображения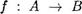 
см. пример 2 с. 60) является эквивалентностью на множестве А.
14. Множество А называется эквивалентным множеству В , если существует биекция р : А В . Этот факт обозначается через А В . Докажите, что отношение 
рефлексивно, симметрично и транзитив но.
15. Докажите, что бинарное отношение, определенное на множестве N х N по правилу
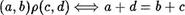
для любых (а, Ь), (с, ф ? N х N, является эквивалентностью.
16. Пусть А— произвольное множество. Тогда А! = AU{c} 
где с А называется множеством, полученным из А присоеДпнением одного элемента. Докажите:
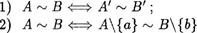для любых множеств А и В. (Определение отношения см. с. 59.)
17. Докажите, что бинарные отношения, определенные на данном множестве, образуют полугруппу с еДиницеб относительно операции композиции.
18. Докажите, что
(а) операция КоМпозИцИи бинарных отношений (определенных на фиксированном множестве) Дистрибу 
тивна относительно операции объеДинения;
(Ь) (аПЏ)от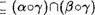 
для любых бинарных отношений а, р, Т, определенных на данном множестве.
19. Докажите, что композиция а о р эквивалентностей а и Д является эквивалентностью тогда и только тогда, когда а о Д = о а .
20. Сколько различных группоидов можно задать на двухэлементном, трехэлементном, и т.д. — на п-элементном множестве.
21. Показать, что если группоид содержит нейтральный элемент, то этот элемент единственен.
22. Укажите, какие из следующих операций на множестве R+ положительных действительных чисел ассоциативны, коммутативны:
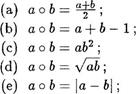
(f) аоЬ— тах{а, b} .
23. Докажите, что множество натуральных чисел относительно каждой из следующих операций является полугруппой:
(а) аоЬ= НОД(а, Ь) 
(Ь) аоЬ= ноща, Ь) 
(с) а о Ь = min{a, Ь} 
(d) аоЬ = а
24. Укажите, какие из следующих множеств образуют полугруппу относительно операции умножения:
25. Пусть Р (А) означает множество всех подмножеств множества А . Какие из следующих операций: (а) пересечение; (Ь) объединение; (с) разность 
определяют полугруппу с носителем Р (А) ?
26. Докажите, что следующие множества образуют группу относительно умножения (т.е. являются МУЛЬТИПЈШКативными группами):
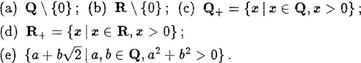
27. Докажите, что следующие множества образуют группу относительно сложения (т. е. являются аддитивными группами) •
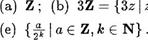= {3zl z e Z} ; (с) Q ; (d) R 
28. Пусть А {1, 2, 3}. Выпишите все подстановки множества А. Составьте таблицу Кэли, соответствующую операции композиции подстановок.
Известно (см. с. 73), что подстановки на множестве А образуют группу (S(A), о) относительно композиции.
Используя составленную Вами таблицу Кэли, покажите, что группа S3 некоммутативна.
Опираясь на полученный результат, попытайтесь доказать, что группа Sn при п > З некоммутативна.
29. Пусть (К; -6, — кольцо. Докажите следующие свойства:
(Ь) Уа, Ь, се К (аф — с) = ab — ас Л (Ь — с)а = Ьа — со).
Гл ав а Ш
Дата: 2019-02-02, просмотров: 299.
