Одной из замечательных особенностей, характеризующих высокий уровень развития математической теории, является возможность ее аксиоматического построения.
Основные идеи и принципы аксиоматической теории были изложены в 7 первой главы.
Ниже приводится один из вариантов аксиоматической теории натуральных чисел, предложенный итальянским математиком Пеано в 1889 г.
Первичными понятиями служат “еДиница” ”натуральное число ” и бинарное отношение ”слеДовать за 
Множество N натуральных чисел в аксиоматике Пеано определяется системой аксиом.
Аксиома Р1 : ” 1 (единица) есть натуральное числю .
В дальнейшем, если натуральное число т следует за натуральным числом п , то мы иногда будем говорить, что ” т является слеДующим за п “ натуральным числом и обозначать этот факт в виде равенства т = п! , т.е. п' является “слеДуюЩИ.М за п ” натуральным числом. В этом случае допускается также фраза: ” число п является преДшествующим для т ” 
Аксиома Р2 : “Для кажДого натурального числа п существует, и притом только одно, натуральное чИсло ту слеДующее за ним“, т.е.
Уа, Ь, с N(b = Ы Л с = а' Ь = с).
Таким образом, соответствие п п' является отображением множества N в N. Другими словами, является унарной операцией на множестве N.
Аксиома Рз : ”ЕДиница не слеДует ни за оДним натуральным числом“, т.е.
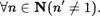
Аксиома РА : ”Если числа т! и , следующие за чИслами т и п, соотв етственно равны, то и сами эти числа равны”, т.е.
Мт, п N(mf т = п).
Аксиома Р5 (аксиома инДутсции): ”Если подмножество М множества натуральныс чисел соДержит еДиницу и вместе с тсажДым натуральньа,и числом п , всоДящим в него, оно соДержит и слеДующее за ним число п! , то оно совпаДает с N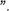 
Таким образом, натуральные числа можно опреДелить как алгебру (N, Е, 1) с оДной унарной операцией F , где F(n) 
— п! Для любого п ? N , и с оДной нульарной операцией 1 при условии выполнения в этой алгебре аксиом Р1 — Р5 
Напомним (гл], 7), что аксиоматическая теория представляет собой множество всес ее теорем. Под словом ”meорема” подразумевается любое слеДствие из аксиом данной теории.
В сложившейся практике некоторые из теорем называются 
леммои , предложением“ или ” следствием“ 
Не существует общих соглашений относительно использования этих названий. Как правило, выбор названия определяется акцентами, которые делаются авторами в зависимости от роли теорем в данной теории.
Название ” теорема“ , как правило, сохраняется за теми следствиями, которые имеют основополагающее значение в том смысле, что доказательства многих других теорем данной теории не могут обойтись без использования данной теоремы в качестве посылки.
Например, знаменитая теорема Пифагора в явном или неявном виде выступает в качестве посылки при вывоДе любого метрического соотношения в треугольнике.
Название “ лемма“ обычно применяется для теоремы, которая выполняет ” техническую“ роль при выводе одной или нескольких ” теорем“ ( т.е. используется в виде ” специфического“ правила вывода в данной теории) 
Приведем несколько теорем, которые непосреДственно следуют из аксиом Пеано.
“ Ближайшие“ следствия из аксиом Пеано
Следствие 1 (первая форма метода математической индукции для натуральных чисел). Пусть Р(с)— оДноместный преДикатп, опреДеленный на множестве N натуральныс чисел. ТогДа, если Р(1) истинно и из преДположения справеДлавости преДиката Р Для произвольного фиксированного на 
турального числа п слеДует справеДливость Р Для слеДующего за ним натурального числа п' , то преДикат Р(с) является тожДественно истинньии на множестве натуральныс чисел.
Таким образом, следующая формула исчисления предикатов
Р(1) Л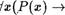 
Р(с')) -4 VcP(c)
является тожДественно истинной для любого предиката, определенного на множестве натуральных чисел.
Д о к а з а т е л ь с т в о. Предположим, что условие следствия 1 выполнено, т.е. истинны оДновременно следующие два высказывания:
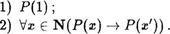
Пусть М означает множество всес натуральныс чисел, для которых предикат Р(с) превращается в истинное высказывание, т.е. М является областью истинности предиката Р(с) . Для доказательства следствия 1 Достаточно установить, что М = N 
Согласно 1) имеем, что 1 ? М , а в силу условия 2) множество М вместе с каждым натуральным числом т содержит следующее за тп число rn' . Отсюда, в силу аксиомы Р5, имеет место равенство М = N . Утверждение доказано.
На практике следствие 1 часто используется в упрощенной формулировке: Для того, чтобы доказать утверждение Р Для всег натуральных чисел, достаточно выполнить два шага:
1-й шаг — проверить, что Р(1) истинно;
2-6 шаг — предположив Р(п) истинным для произвольного фиксированного натурального числа п , показать, что Р(п') истинно.“
Последовательность, состоящую из этих двух шагов, называют метоДом математической инДукции (в первой форме).
Следствие 2. Всякое натуральное число, отличное от еДиницы, является слеДующим за некоторым натуральным числом.
Д о к а з а т е л ь с т в о. Обозначим через Р (п) предикат
п 1 Втп(п = ты) 
Очевидно, что Р(п) равносилен предикату
п = 1 V Вт(п = т!) 
Нужно доказать, что этот предикат является тожДественно истинным на множестве натуральных чисел.
Применим метоД математической инДукции:
1-й шаг. Очевидно, что этот предикат является истинным высказыванием при п = 1 .
2-6 шаг. Предположим, что предикат Р (п) = И, где п (- N , т.е. п = 1 либо п = т! для некоторого т ? N . Тогда п! , по определению, является слеДующим за п , т.е. утверждение верно для . Доказательство закончено.
Следствие З. Всякое натуральное число не равно следующему за ним натуральному числу, т.е. п Для любого числа п ? N 
Д о к а з а т е л ь с т в о. Применим метоД математической инДукции:
1-6 шаг. При п 1, в силу аксиомы Рз, утверждение верно.
2-й шаг. Нужно доказать, что высказывание
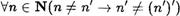
истинно. От противного. Пусть п п! лп' — ' для некоторого п N . Из равенства п! (п ) , по аксиоме Р4, получаем, что п = , что, очевидно, противоречит неравенству п п! 
Утверждение доказано.
В формулировке следствия 4 встречается термин ”бесконечное множество". Множество называется бесконечным, если оно не является конечным.
Чтобы сформулировать определение конечного множества, напомним необходимые понятия.
Подмножество В множества А называется его правильной частью, если В А. Эквивалентными называют такие два множества, для которых существует биекция одного из них на другое (упражнение 14, 12, гл.П).
Множество называется конечным, если оно не может быть эквивалентным своей правильной части.
Следствие 4. Множество N натуральныс чисел бесконечно.
Д о к а з а т е л ь с т в о. В силу сказанного, перед формулировкой данного следствия нам достаточно установить, что множество N эквивалентно своей правильной части.
Положим Nl = N {1} . Тогда соответствие F :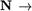 
N1 , при котором F(n) — является отображением, в силу аксиом Р2 и Рз 
Действительно, ввиду аксиомы Р2, каждый элемент из N имеет, и притом только один, образ, а из аксиомы Рз следует, что Р (п) ? N1 для любого п (- N 
Аксиома Р4 обеспечивает инъективность отображения F а сюръективность F вытекает из следствия З.
Таким образом, множество N эквивалентно подмножеству Nl . Осталось заметить, что N1 — правильная часть множества N, поскольку 1 N1 
2. Сложение и умножение натуральных чисел
Определение. Сложением натуральныс чисел называется бинарная операция Т , опреДеленная на множестве N и уДовлетворяющая СЛеДуюЩИМ условиям (аксиомам сложения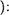 
1) е N(nT1 = п ) 
2) Уп, т ? N(nTmf (пТт)') .
Теорема. Сложение натуральныс чисел существует и еДинственно.
Д о к а з а т е л ь с т в о.
1. Существование сложения.
По определению. нам необходимо доказать существование отображения
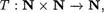
для которого выполняются условия 1) и 2) 
Представим множество N х N в виде N х N = U Ni , где
(т.е. пара (т, п) ? Ni тогда и только тогда, когда т = i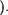 
Построим сначала последовательность отображений Т; : М — ГЧ (i e N),
каждое из которйх удовлетворяет условиям 1) и 2), т.е.
1) iTi1 = i',
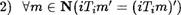
для каждого i ?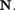 
Существование такой последовательности отображений будем доказывать методом математической индукции по номеру i члена последовательности 1'i .
Пусть i — 1 . Отображение Т1 : N1 N определим следующим образом:
положим, по определению,
1т1п = для каждого п (- N.
Проверим, что 111 удовлетворяет условиям 1) и 2).
По определению, 11'11 1' , т.е. условие 1) выполняется.
Далее, 11'1п' по определению 111 , откуда, используя это определение снова, получим. что 1 т'1п' = (1т1п)' , т.е. условие 2) также выполнено для 111 
Таким образом, первый шаг индукции сделан.
Предположим теперь, что для некоторого натурального числа п существует отображение Тп , удовлетворяющее условиям:
пТп1 2.: (3)
птптп' (пТпт)'. (4)
Используя отображение Тп , определим отображение ТЫ по правилу п'ттџтп (пТпт)'. (5)
Покажем, что отображение Тп' также удовлетворяет условиям 1) и 2).
Действительно, в силу 3) имеем 1 (птп1)' , откуда, поскольку отображение Тп удовлетворяет условию 1), то (птп1)” = и, значит, п'Тп'1 (п ) 
Последнее равенство, в свою очередь, означает, что отображение Тт; удовлетворяет условию 1).
Покажем, что отображение Та! удовлетворяет условию 2). По определению (5), имеем n'1'ntm' — (пТптп')' откуда в силу
(4) следует
” п ” = ((nTnm)')' — (п!Ттџт)'
(последнее равенство имеет место в силу (5) ). Это „означает, что отображение Та! удовлетворяет условию 2).
Таким образом, послеДовательность отображений Тп (п ? N), удовлетворяющая условиям 1) и 2), существует.
Пользуясь теперь этой последовательностью, определим операцию Т на множестве N, полагая, по определению, аТЬ — — аТаЬ для любых чисел а, Ь ? N 
Проверим, что операция Т удовлетворяет условиям 1) и 2) 
1) По определению, аТ1 г: аТа1 = а' (последнее равенство верно в силу того, что отображение Та обладает этим свойством для любого а ? N 
2) Снова по определению получим, что аТЫ атаы 
= (атаб)' — - (аТЬ)' для любых чисел а, Ь е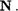 
Таким образом, сложение существует. П. ЕДинственность сложения.
Пусть Т и Е— две операции, удовлетворяющие условиям 1) и 2) в определении сложения, т.е.
Уа е N(aT1 = а!) 
| (6) |
| Уа, е N(aTb' = (ать)'), | (7) |
Уа е N(aF1 Ы) 
| (8) |
| Уа, ь е N(aFb' = (aFb)'). | (9) |
Докажем, что операции Т и F совпаДают, т.е.
аТЬ ан (10)
для любых элементов а, Ь ? N 
Зафиксируем произвольный элемент а ? N . Тогда формула (10) будет одноместным предикатом от переменной Ь . Поэтому будем Доказывать это равенство инДукциетЈ по Ь (при фиксированном а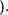 
1. Пусть Ь = 1 . Тогда из (6) и (8) следует: аТ1 = а! = ар 1 
т.е. утверждение (10) верно при Ь = 1 
2. Предположим, что аТп = aFn для некоторого п е N .
Тогда, используя (7) и (9), получим атп' = (аТп)' — (aFn)' = aFn' 
т.е. равенство (10) имеет место и при Ь = ту 
Таким образом, равенство (10) справедливо Для любого элемента Ь и фиксированного элемента а . Но поскольку а выбирался произвольным, то это равенство имеет место для любых чисел а, Ь ? N 
Поскольку сложение единственно, то для него можно ввести станДартныб знак ” + ” . Результат сложения а + Ь в дальнейшем будем называть суммоб.
С войс т в а сл о ж е н и я
Из определения операции сложения непосредственно вытекают свойства:
1) Ма N(a+ 1 = Ж).
2) va,b ? N(a+b'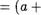 
Из доказательства теоремы существования и единственности сложения имеем:
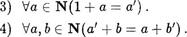
5) Сложение натуральныс чисел коммутативно, т.е.
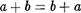(11)
для любых элементов а, Ь ? N 
Проведем доказательство этого равенства инДукцией по элементу Ь (при фиксированном а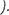 
Пусть Ь 1 . Тогда в силу свойств 1 и З получим а + 1 = 
а! 1 + а , т.е. равенство (11) при Ь = 1 верно.
Предположим, что оно справедливо при Ь п, т.е. а-{-п 
п + а— верно.
Докажем справедливость равенства (11) при Ь = п! 
Из (1) имеем а + п' (а + п)' , откуда в силу инДуктивного преДположения (т.е. в силу равенства а 4- п = п + б) получим
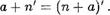
По свойству 2 имеем (п + а)! = п + а! , откуда в силу свойства 4 вытекает, что (п + ау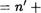 
Отсюда, используя равенство а+п' (п+а)' , получим, что а + п! + а. Это означает, что равенство (11) справедливо при Ь п! 
Теперь, учитывая, что число а выбиралось произвольно, приходим к выводу, что равенство (11) справедливо для любых
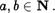
6) Сложение натуральныс чисел ассоциативно, т.е.
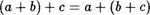(12) для любых а, Ь, с ? N .
Д о к а з а т е л ь с т в о. Зафиксируем произвольные числа а, Ь и провеДем инДукцию по с.
Пусть с = 1 . Тогда по свойству 1 имеем (a+b)+1 (a-Fb) f 
С другой стороны, (а + Ь)! — а + Ы по свойству 2. Отсюда
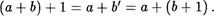
Таким образом, при с — 1 равенство (12) верно.
Предположим теперь, что
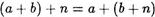
для некоторого числа п N 
Докажем, что равенство (12) верно при с = п! .
Согласно свойству 2 справедливо равенство (а + Ь) + — — ((а + Ь) + п)! , откуда в силу индуктивного предположения получаем
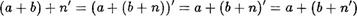
(последние два равенства в этой цепи справедливы в силу свойства 2).
Таким образом, (а + Ь) + п' а + (Ь + . Утверждение доказано.
7) Сложение уДовлетворяет законам сокращения:
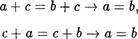(13)
для любых чисел а, Ь, с N 
Д о к а з а т е л ь с т в о. Поскольку сложение коммутативно, то достаточно доказать только первую импликацию.
Зафиксируем числа а, Ь . Тогда формула
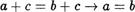
будет одноместным предикатом от переменной с . Проведем индукцию по с.
Пусть с = 1 и а + 1 = Ь + 1 , т.е. а! — Ы Тогда а = Ь по аксиоме Р4. Таким образом, формула (13) верна при с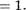 
Предположим, что импликация (13) верна при с = п, т.е. из а + п = Ь + п следует а = Ь.
Докажем справедливость импликации
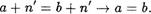
Пусть а + п! = b+n' . Тогда (а + п)! (Ь + п)' в силу свойства 2, откуда по аксиоме Р4 следует а+п = b+n и, далее, по индуктивному предположению получим а = Ь . Утверждение доказано.
Замечание. Алгебра -е) является коммутативной полугруппой, в которой выполняется закон сокращения.
Эта полугруппа называется аДДитивной полугруппой натуральных чисел.
Умножение натуральных чисел
Определение. Умножением натуральных чисел называется бинарная операция П , опреДеленная на множестве N натуральныс чисел и уДовлетворяющая слеДующим условиям аксиомы умножения 
1') а П 1 = а Для любого а Е N;
2') а П Ы = а П Ь + а Для любыс а, Ь N.
Теорема (существования и единственности умножения) 
Умножение натуральныс чисел существует и еДинственно.
Д о к а з а т е л ь с т в о этой теоремы проводится по той же схеме, что и доказательство соответствующей теоремы сложения. При этом, очевидно, нужно заменить всюду символ Т на П и произвести коррективы с учетом условий 1') и 2'). Например, вместо равенства 1131 п = п! записать 1 ГЛ1 п = п , а равенство (5) заменить равенством
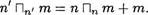(5')
Предоставляем читателю провести это доказательство в качестве упражнения.
В дальнейшем для обозначения операции умножения используется стандартный знак • (точка). Результат а ПЬ умножения называется произвеДением чисел а и Ь и обозначается через а • Ь либо — ab 
Дата: 2019-02-02, просмотров: 240.
