Для расчета скалярного полинома скалярной переменной (2.7) известна схема Горнера [3], при использовании которой уменьшается алгоритмическая сложность и повышается точность расчетов. В связи с этим представляется целесообразной разработка такой же схемы для скалярного полинома векторной переменной (2.8) или вообще для многомерно-матричного полинома (2.6). Получим схему Горнера сразу для многомерно-матричного полинома (2.6). Для этого запишем его в развернутой форме

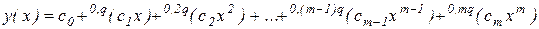(2.10)

и представим в виде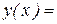

.

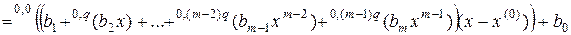(2.11)

Раскроем скобки в (2.11). Для иллюстрации выполним это для отдельного слагаемого в (2.11)

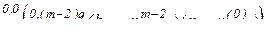
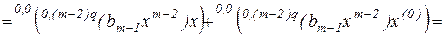
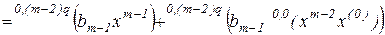.                   (2.12)

Учитывая симметричность матрицы 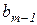 относительно последних мультииндексов, можно показать (см. приложение), что

,

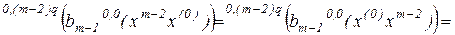
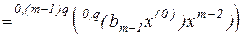и вместо (2.12) получим

.

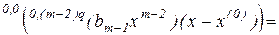
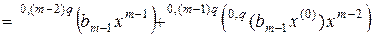Этот результат позволяет нам после раскрытия скобок в (2.11) приравнять коэффициенты полиномов (2.10) и (2.11). В итоге получим соотношения

,

,

………………………………

,

………………………………

.

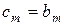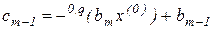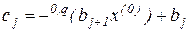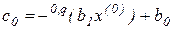Отсюда получаем алгоритм

,

, .

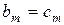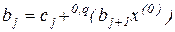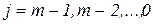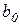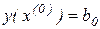Если учесть, что в конце расчетов по данному алгоритму мы получаем коэффициент  и что , то становится ясно, что мы получили алгоритм расчета значения многомерно-матричного полинома (2.6) в точке 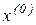. Ввиду произвольности  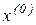верхний индекс в обозначении этой точки можно опустить. В итоге получаем следующий алгоритм расчета значения полинома (2.6) в любой точке :

,

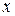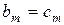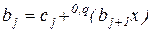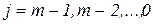, ,                   (2.13)

.

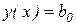Это и есть схема Горнера для многомерно-матричного полинома (2.6).

Схема Горнера реализована в пакете программ «Анализ многомерных данных» для расчета значений скалярного полинома векторной переменной произвольной степени.

Порядок выполнения работы

2.3.1. Запрограммировать расчет скалярного полинома ( 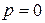) векторной переменной ( 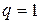) по выражениям (2.3) и (2.8) в случае двух переменных ( 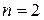). Варианты заданий приведены в табл. 2.1. Вывести в одно графическое окно трехмерный и контурный графики полинома (2.3), а в другое – трехмерный и контурный графики полинома (2.8) (с помощью функции meshc).

Указание. Исходный полином задать в классическом представлении (2.3), выбрав коэффициенты 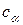 и степени  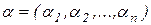его переменных самостоятельно, а его многомерно-матричные коэффициенты в представлении (2.8) сформировать вручную путем сопоставления коэффициентов при одинаковых степенях переменных в классической и многомерно-матричной формах представления. Для такого сопоставления целесообразно записать эти две формы представления на бумаге. При правильном сопоставлении коэффициентов полинома двух форм представления (2.3) и (2.8) трехмерные графики в п. 2.3.1 должны совпадать. Для расчета значений полинома в многомерно-матричном представлении можно воспользоваться как непосредственно определением (2.8), так и схемой Горнера (2.13) (по выбору студента).

Таблица 2.1

№ варианта	Степень полинома	№ варианта	Степень полинома	№ варианта	Степень полинома
1.	3	11.	3	21.	3
2.	2	12.	4	22.	2
3.	3	13.	3	23.	3
4.	4	14.	2	24.	4
5.	5	15.	3	25.	3
6.	2	16.	4	26.	2
7.	3	17.	3	27.	3
8.	4	18.	2	28.	4
9.	3	19.	3	29.	3
10.	2	20.	4	30.	5

ЛИТЕРАТУРА

1. Муха, В.С. Анализ многомерных данных: Монография / В.С. Муха. – Мн.: Технопринт, 2004. – 368 с.

2. Муха, В.С. Анализ многомерных данных: Лабораторный практикум / В.С. Муха, К.С. Корчиц. – Мн.: БГУИР, 2005. – 56 с.

3. Соколов, Н.П. Введение в теорию многомерных матриц / Н.П. Соколов. – Киев: Наукова думка, 1972. – 175 с.

4. Калюжнин, Л.А. Преобразования и перестановки / Л.А. Калюжнин, В.И. Сущанский. – М.: Наука, 1979. – 112 с.

5. Муха, В.С. Введение в MATLAB: Метод. пособие для выполнения лаб. работ по курсам "Статистические методы обработки данных" и "Теория автоматического управления" для спец. 53 01 02 "Автоматизированные системы обработки информации" / В.С. Муха, В.А. Птичкин. – Мн.: БГУИР, 2002. – 40 с.

6. Дьяконов, В.П. MATLAB 5.0/5.3. Система символьной математики / В.П. Дьяконов, И.В. Абраменкова. – М.: Нолидж. – 1999. – 740 с.

7. Муха, В.С. Теория вероятностей: Учеб. пособие для студентов технических специальностей высших учебных заведений / В.С. Муха. – Мн.: БГУИР, 2001. – 167 с.

КОНТРОЛЬ ЗНАНИЙ

Вопросы к экзамену по курсу "Анализ многомерных данных"

1. Классический подход к анализу данных: правила дифференцирования функции одной переменной, ряд Тейлора для функции одной переменной.

2.  Классический подход к анализу многомерных данных: правила дифференцирования функций многих переменных.

3.  Классический подход к анализу многомерных данных: ряд Тейлора для функции многих переменных.

4.  Подход функционального анализа к анализу многомерных данных: линейное пространство, метрическое пространство, нормированное пространство, евклидово пространство.

5.  Подход функционального анализа к анализу многомерных данных: операторы в линейных пространствах, линейный оператор, обратный оператор, сумма операторов, суперпозиция операторов.

6.  Подход функционального анализа к анализу многомерных данных: непрерывный оператор, дифференцируемый оператор, производная Фреше, ряд Тейлора для дифференцируемого отображения.

7.  Векторно-матричный подход к анализу многомерных данных: понятие матрицы и вектора, транспонирование матрицы, сложение, умножение матриц, умножение матрицы на число.

8.  Векторно-матричный подход к анализу многомерных данных: определитель, след матрицы, обратная матрица, присоединенная матрица, транспонирование произведений матриц.

9.  Векторно-матричный подход к анализу многомерных данных: дифференцирование, интегрирование матриц, зависящих от скалярного аргумента.

10.  Векторно-матричный подход к анализу многомерных данных: дифференцирование скалярной функции по векторному и матричному аргументам, дифференцирование векторной функции по векторному аргументу.

11.  Векторно-матричный подход к анализу многомерных данных: ряд Тейлора для функции векторной переменной.

12.  Определение многомерной матрицы, симметричные многомерные матрицы.

13.  Операции над многомерными матрицами (сложение, умножение на число, ( 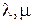)-свернутое умножение).

14.  Частные случаи умножения многомерных матриц.

15.  Многомерные единичные матрицы.

16.  Матрицы, ассоциированные с многомерными матрицами. Теорема о произведении ассоциированных матриц.

17.  Многомерные обратные матрицы.

18.  Многомерно-матричные системы линейных алгебраических уравнений.

19.  Подстановки (перестановки): определение, суперпозиция подстановок, тождественная, обратная подстановки, подстановки типа "вперед", "назад", "вперед-назад".

20.  Транспонирование многомерных матриц: определение транспонированной матрицы, повторное транспонирование матрицы.

21.  Транспонирование ( 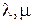)-свернутого произведения многомерных матриц.

22.  Определение многомерно-матричной производной, основные правила дифференцирования.

23.  Производные некоторых многомерно-матричных функций.

24.  Представление многомерно-матричной функции рядом Тейлора.

25.  Определение многомерной случайной матрицы, законы распределения многомерной случайной матрицы.

26.  Начальные и центральные моменты многомерной случайной матрицы.

27.  Математическое ожидание, дисперсионная матрица многомерной случайной матрицы, их свойства.

28. Формулы связи между начальными и центральными моментами многомерной случайной матрицы.

29. Нормально распределенные многомерные случайные матрицы.

30. Многомерные случайные матрицы с совместным нормальным распределением.

31.  Принятие решения о многомерной случайной матрице по наблюдению другой многомерной случайной матрицы, случай квадратичной функции потерь.

32. Многомерная модель данных и OLAP-системы.