Цель работы
1. Изучение полиномов многих переменных на основе системы Matlab.
Теоретические положения
Классические полиномы многих переменных
Рассмотрим классическую форму представления скалярного полинома 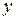 многих переменных
многих переменных 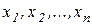 , или, иначе, скалярного полинома
, или, иначе, скалярного полинома 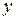 векторной переменной
векторной переменной 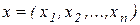 . Вектор
. Вектор 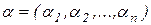 с целочисленными неотрицательными компонентами назовем мультииндексом и обозначим
с целочисленными неотрицательными компонентами назовем мультииндексом и обозначим 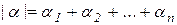 . Скалярная функция
. Скалярная функция  переменных
переменных 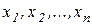 вида
вида
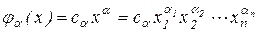 ,
, 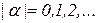 , (2.1)
, (2.1)
называется одночленом  переменных степени
переменных степени 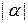 . Скалярная функция вида
. Скалярная функция вида
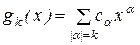 (2.2)
(2.2)
называется однородным полиномом степени  векторной переменной
векторной переменной 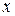 . Скалярная функция вида
. Скалярная функция вида

называется полиномом степени 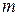 векторной переменной
векторной переменной 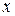 . Таким образом, полином степени
. Таким образом, полином степени 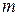 векторной переменной
векторной переменной 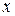 представляет собой сумму однородных полиномов (2.2) или сумму одночленов вида (2.1) со степенями от
представляет собой сумму однородных полиномов (2.2) или сумму одночленов вида (2.1) со степенями от 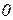 до
до 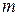 :
:
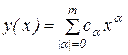 . (2.3)
. (2.3)
Например, классическое представление скалярного полинома второй степени трех переменных 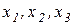 имеет вид
имеет вид
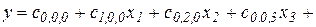
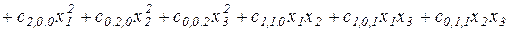 . (2.4)
. (2.4)
Если ввести здесь однородные полиномы степеней 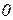 ,
, 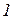 ,
, 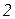
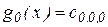 ,
,
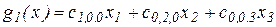 ,
,
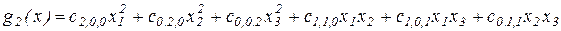 ,
,
то этот полином будет иметь вид
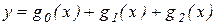 .
.
Важно знать, сколько одночленов содержит однородный полином степени 
 переменных (2.2) и полином
переменных (2.2) и полином  переменных степени
переменных степени 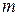 (2.3). Очевидно, что эти полиномы имеют столько же коэффициентов. Однородный полином степени
(2.3). Очевидно, что эти полиномы имеют столько же коэффициентов. Однородный полином степени 
 переменных (2.2) содержит
переменных (2.2) содержит
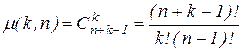
одночленов (коэффициентов). Полином  переменных степени
переменных степени 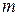 (2.3) содержит
(2.3) содержит
 .
.
одночленов (коэффициентов). Ясно, что
 .
.
В частности, для полинома второй степени трех переменных (2.4) имеем
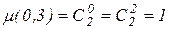 ,
,
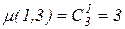 ,
,
 ,
,
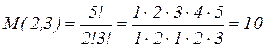 .
.
Для сравнения, число коэффициентов полинома 2-й степени четырех переменных будет равно
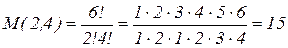 .
.
Неудобство работы с полиномами многих переменных в классической форме (2.3) состоит в плохой формализованности этого выражения. Плохая формализованность заключается в том, что порядковый номер коэффициента 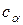 в сумме (2.3) не совпадает с его «официальным номером»
в сумме (2.3) не совпадает с его «официальным номером» 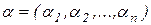 . Для преодоления этих трудностей необходимо иметь способ упорядочивания мультииндексных номеров
. Для преодоления этих трудностей необходимо иметь способ упорядочивания мультииндексных номеров 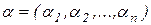 как для фиксированного числа
как для фиксированного числа 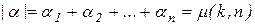 , так и для всех
, так и для всех 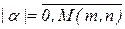 . Наиболее часто применяется так называемое лексикографическое упорядочивание, определение которого также плохо формализовано. Из названия такого упорядочивания следует, что оно рассчитано на лексикографические способности человека и выполняется вручную. При отсутствии компьютерного алгоритма упорядочивания для однозначного определения полинома многих переменных (2.3) необходимо задавать не его коэффициенты
. Наиболее часто применяется так называемое лексикографическое упорядочивание, определение которого также плохо формализовано. Из названия такого упорядочивания следует, что оно рассчитано на лексикографические способности человека и выполняется вручную. При отсутствии компьютерного алгоритма упорядочивания для однозначного определения полинома многих переменных (2.3) необходимо задавать не его коэффициенты 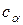 , а таблицу соответствий порядковых номеров коэффициентов значениям коэффициентов и значениям их мультииндексов
, а таблицу соответствий порядковых номеров коэффициентов значениям коэффициентов и значениям их мультииндексов 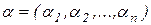 .
.
Дата: 2019-02-02, просмотров: 523.