Цель работы
2.1.1. Изучение аппроксимации функции многих переменных отрезками ряда Тейлора с помощью многомерно-матричного подхода и исследование ее точности.
Теоретические положения
Многомерно-матричный ряд Тейлора для скалярной функции векторной переменной
Многомерно-матричный ряд Тейлора для скалярной функции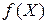 
векторной переменной 
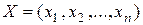в окрестности точки 
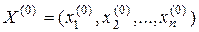имеет вид:
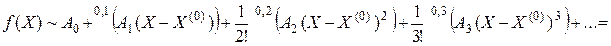
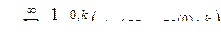, (2.1)
где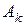 
, 
– 
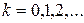-мерные матрицы 
-го порядка, симметричные при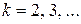 
. Они определяются выражениями:
,
, 
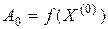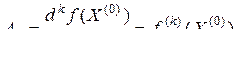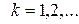, (2.2)
т.е. представляют собой многомерно-матричные производные функции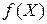 
, вычисленные в точке разложения 
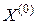. Обозначение 
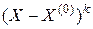означает 
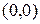-свернутую -ю степень вектора 
.
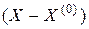Производная скалярной функции 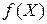векторной переменной 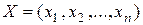определяется выражением
, 
,
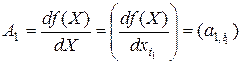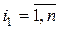т.е. представляет собой вектор длины (одномерную матрицу -го порядка). Производные высших порядков определяются последовательным дифференцированием:
, 
.
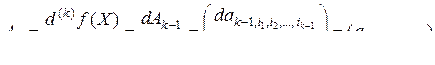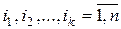Правила многомерно-матричного дифференцирования
Справедливы следующие правила многомерно-матричного дифференцирования [2, 3].
1. Производная сложной функции. Пусть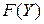 
– многомерно-матричная функция ( 
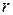-мерная матрица)
– 
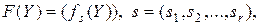
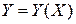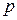-мерная матрица,
– 
-мерная матрица с различными (несовпадающими) элементами,
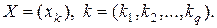
Тогда производная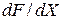 
определяется как следующее 
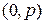-свернутое произведение:
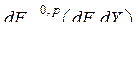
2. Производная произведения. Пусть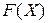 
– 
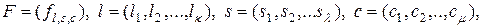
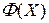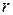-мерная матрица,
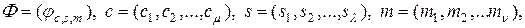
– -мерная матрица,
– -мерная матрица,
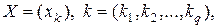
причем 
, 
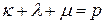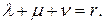Справедлива следующая формула дифференцирования 
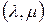-свернутого произведения матриц 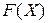и :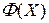
.
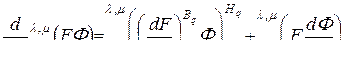Здесь символам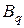и 
и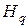 
обозначены подстановки типа «вперед» и «назад» на 
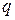индексов соответственно. Общее количество индексов подстановок 
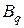и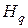 
равно размерности транспонируемых матриц.
3. Производная неявной функции. Пусть функция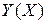 
задана неявно равенством
,
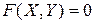где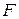 
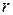– -мерная матрица,
,
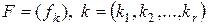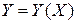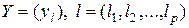– -мерная матрица,
,
– -мерная матрица,
.
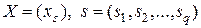Тогда производная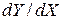 
есть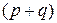 
-мерная матрица, которая находится как решение следующего многомерно-матричного уравнения
.
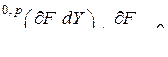4. Производная транспонированной матрицы. Пусть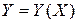 
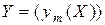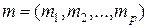– -мерная матрица,
, 
,
– -мерная матрица,
.
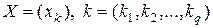Справедливо следующее равенство.
,
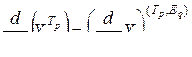где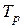 
– некоторая произвольная подстановка на 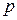индексах 
, 
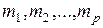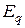– тождественная подстановка на индексах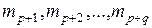 
.
Замечание. В рассматриваемом нами случае функции 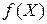векторной переменной аргумент 
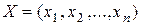является одномерной матрицей -го порядка, т.е. в приведенных выше правилах дифференцирования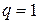 
.
Пример
Приведем пример представления скалярной функции двух переменных многомерно-матричным рядом Тейлора. Рассмотрим функцию
,
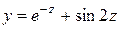где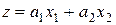 
. В этом случае мы имеем скалярную функцию двух переменных 
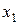и 
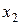(одномерной матрицы второго порядка 
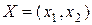). Если ввести одномерную матрицу коэффициентов 
, то
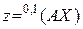и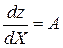 
. Будем рассматривать разложение в ряд Тейлора в окрестности точки 
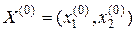. Обозначим
.
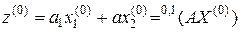Тогда
,
.
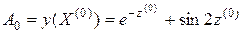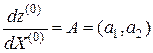Заметим, что любая скалярная функция переменной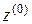 
может перемещаться в многомерно-матричных произведениях в любое место как скалярная величина. Найдем коэффициенты 
, 
, 
, 
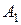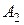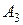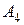(2.2) ряда Тейлора (2.1). Получим
,
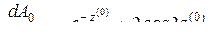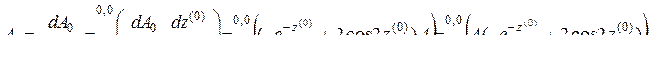В последнем выражении мы изменили место функции 
в произведении на основании сказанного выше. Этим приемом будем пользоваться и в дальнейшем. Далее, так как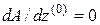 
, то
,
,
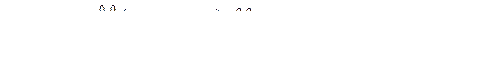
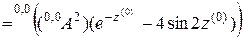где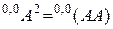 
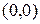– -свернутый квадрат матрицы 
. Продолжим дифференцирование для поиска коэффициентов 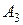, 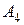(2.2).
,
,
.
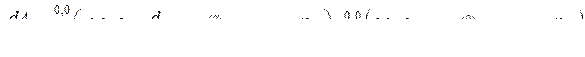
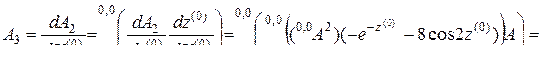
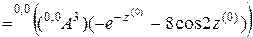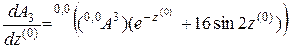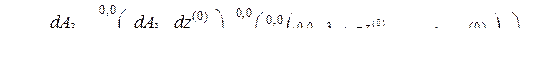
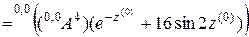Отрезок ряда Тейлора для рассмотренной функции имеет вид
.
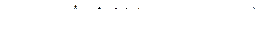Порядок выполнения работы
2.3.1. Выбрать функцию из таблицы 1.2 в соответствии с номером своего варианта, представив в ней скалярный аргумент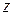 
в виде полинома 1-й или 2-й степени переменных 
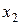, , например, в виде 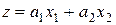, или в виде
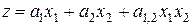, (2.3)
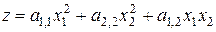, (2.4)
и т.д. Для полученной таким образом функции двух переменных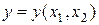 
найти матрицы производных (2.2) до третьего порядка включительно. Воспользоваться при этом приведенными правилами многомерно-матричного дифференцирования [2, 3], оформив выбранную функцию 
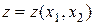как промежуточную многомерно-матричную переменную. Например, для линейной функции 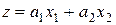нужно ввести матрицы , 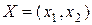и записать ее в виде 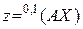. Для квадратичных функций (2.3), (2.4) нужно дополнительно ввести симметричную матрицу коэффициентов
, 
,
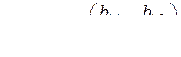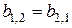и записать эти функции в виде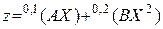 
, , 
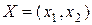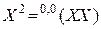. При расчетах для получения функции (2.3) необходимо задать матрицу 
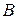в виде
.
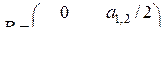Для получения функции (2.4) матрицу необходимо выбрать нулевой, а матрицу 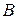определить в виде
,
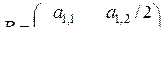т.е. записать функцию (2.4) в виде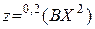 
. С помощью варьирования значений матриц и 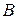можно задавать другие функции двух переменных.
2.3.2. Написать m-файл-сценарий для аппроксимации данной функции двух переменных отрезками ряда Тейлора (2.1) в окрестности некоторой самостоятельно выбранной точки. В одно графическое окно с помощью программы mesh вывести графики функции и аппроксимирующих полиномов. Проанализировать точность аппроксимации при различном числе слагаемых ряда Тейлора.
2.3.3. Оформить отчет, в котором привести функцию двух переменных, ее многомерно-матричные производные и полученный отрезок ряда Тейлора.
ЛИТЕРАТУРА
1. Муха, В.С. Анализ многомерных данных: Монография / В.С. Муха. – Мн.: Технопринт, 2004. – 368 с.
2. Муха, В.С. Анализ многомерных данных: Лабораторный практикум / В.С. Муха. – Мн.: БГУИР, 2005. – 56 с.
3. Соколов, Н.П. Введение в теорию многомерных матриц / Н.П. Соколов. – Киев: Наукова думка, 1972. – 175 с.
4. Калюжнин, Л.А. Преобразования и перестановки / Л.А. Калюжнин, В.И. Сущанский. – М.: Наука, 1979. – 112 с.
5. Муха, В.С. Введение в MATLAB: Метод. пособие для выполнения лаб. работ по курсам "Статистические методы обработки данных" и "Теория автоматического управления" для спец. 53 01 02 "Автоматизированные системы обработки информации" / В.С. Муха, В.А. Птичкин. – Мн.: БГУИР, 2002. – 40 с.
6. Дьяконов, В.П. MATLAB 5.0/5.3. Система символьной математики / В.П. Дьяконов, И.В. Абраменкова. – М.: Нолидж. – 1999. – 740 с.
7. Муха, В.С. Теория вероятностей: Учеб. пособие для студентов технических специальностей высших учебных заведений / В.С. Муха. – Мн.: БГУИР, 2001. – 167 с.
Анализ многомерных данных
Контрольные работы для студентов специальности 1 53 01 02
"Автоматизированные системы обработки информации"
дистанционной формы обучения
Указания к выбору варианта
Выполните контрольные работы по двум темам. Варианты возьмите из таблицы 1.0 в соответствии с последними двумя цифрами номера зачетки, отделенными дефисом. Если номер зачетки не содержит таких двух цифр, то обратитесь за вариантом к преподавателю. Отчет по каждой теме пришлите в виде отдельной папки, содержащей программы (m -файлы), отвечающие на каждый пункт "порядка выполнения работы". Имена файлов должны содержать номер пункта задания, например, файл с именем prog2_3_1.m решает задачи пункта 2.3.1 задания по теме 2. Если работа не зачтена, т.е. по ней имеются замечания, то присылайте работу целиком, включая и зачтенные вопросы (новую папку). Старая папка будет заменена новой и выполнена проверка.
Таблица 1.0
Номера вариантов контрольных работ
| Последние две цифры зачетки | Вариант контрольной работы 1 по таблице 1.1 | Вариант контрольной работы 2 по таблице 2.1 |
| [ 1] | '1.29' | '2.07' |
| [ 2] | '1.19' | '2.15' |
| [ 3] | '1.27' | '2.23' |
| [ 4] | '1.14' | '2.01' |
| [ 5] | '1.25' | '2.14' |
| [ 6] | '1.19' | '2.24' |
| [ 7] | '1.28' | '2.23' |
| [ 8] | '1.06' | '2.13' |
| [ 9] | '1.29' | '2.28' |
| [ 10] | '1.13' | '2.27' |
| [ 11] | '1.02' | '2.11' |
| [ 12] | '1.25' | '2.01' |
| [ 13] | '1.05' | '2.07' |
| [ 14] | '1.06' | '2.19' |
| [ 15] | '1.09' | '2.06' |
| [ 16] | '1.01' | '2.23' |
| [ 17] | '1.14' | '2.28' |
| [ 18] | '1.15' | '2.13' |
| [ 19] | '1.26' | '2.16' |
| [ 20] | '1.07' | '2.21' |
| [ 21] | '1.26' | '2.01' |
| [ 22] | '1.21' | '2.12' |
| [ 23] | '1.25' | '2.16' |
| [ 24] | '1.22' | '2.13' |
| [ 25] | '1.10' | '2.06' |
| [ 26] | '1.06' | '2.21' |
| [ 27] | '1.10' | '2.17' |
| [ 28] | '1.05' | '2.21' |
| [ 29] | '1.12' | '2.26' |
| [ 30] | '1.26' | '2.18' |
| [ 31] | '1.15' | '2.27' |
| [ 32] | '1.25' | '2.20' |
| [ 33] | '1.25' | '2.20' |
| [ 34] | '1.21' | '2.09' |
| [ 35] | '1.11' | '2.17' |
| [ 36] | '1.22' | '2.10' |
| [ 37] | '1.26' | '2.18' |
| [ 38] | '1.12' | '2.22' |
| [ 39] | '1.17' | '2.14' |
| [ 40] | '1.21' | '2.19' |
| [ 41] | '1.24' | '2.29' |
| [ 42] | '1.16' | '2.27' |
| [ 43] | '1.06' | '2.30' |
| [ 44] | '1.09' | '2.08' |
| [ 45] | '1.27' | '2.23' |
| [ 46] | '1.05' | '2.01' |
| [ 47] | '1.27' | '2.06' |
| [ 48] | '1.09' | '2.20' |
| [ 49] | '1.09' | '2.15' |
| [ 50] | '1.02' | '2.30' |
| [ 51] | '1.18' | '2.13' |
| [ 52] | '1.16' | '2.11' |
| [ 53] | '1.13' | '2.07' |
| [ 54] | '1.18' | '2.23' |
| [ 55] | '1.16' | '2.20' |
| [ 56] | '1.07' | '2.12' |
| [ 57] | '1.24' | '2.21' |
| [ 58] | '1.14' | '2.18' |
| [ 59] | '1.25' | '2.22' |
| [ 60] | '1.19' | '2.02' |
| [ 61] | '1.13' | '2.10' |
| [ 62] | '1.27' | '2.01' |
| [ 63] | '1.24' | '2.30' |
| [ 64] | '1.30' | '2.24' |
| [ 65] | '1.14' | '2.15' |
| [ 66] | '1.07' | '2.20' |
| [ 67] | '1.10' | '2.29' |
| [ 68] | '1.22' | '2.13' |
| [ 69] | '1.23' | '2.09' |
| [ 70] | '1.14' | '2.29' |
| [ 71] | '1.21' | '2.07' |
| [ 72] | '1.26' | '2.19' |
| [ 73] | '1.05' | '2.07' |
| [ 74] | '1.19' | '2.19' |
| [ 75] | '1.12' | '2.18' |
| [ 76] | '1.14' | '2.02' |
| [ 77] | '1.01' | '2.10' |
| [ 78] | '1.11' | '2.12' |
| [ 79] | '1.21' | '2.03' |
| [ 80] | '1.02' | '2.19' |
| [ 81] | '1.19' | '2.01' |
| [ 82] | '1.01' | '2.06' |
| [ 83] | '1.18' | '2.02' |
| [ 84] | '1.12' | '2.19' |
| [ 85] | '1.22' | '2.21' |
| [ 86] | '1.03' | '2.14' |
| [ 87] | '1.14' | '2.11' |
| [ 88] | '1.05' | '2.21' |
| [ 89] | '1.21' | '2.22' |
| [ 90] | '1.15' | '2.17' |
| [ 91] | '1.04' | '2.14' |
| [ 92] | '1.22' | '2.27' |
| [ 93] | '1.09' | '2.08' |
| [ 94] | '1.26' | '2.07' |
| [ 95] | '1.25' | '2.28' |
| [ 96] | '1.07' | '2.08' |
| [ 97] | '1.02' | '2.03' |
| [ 98] | '1.20' | '2.16' |
| [ 99] | '1.26' | '2.06' |
Дата: 2019-02-02, просмотров: 582.
