Многомерные массивы характеризуются размерностью более двух. Под размерностью массивов понимается число измерений в пространственном представлении массивов, а под размером – произведение числа элементов в каждой размерности массива. Произвольный элемент многомерного массива задается указанием имени массива и индексов в круглых скобках за именем, разделенных запятыми. Например, произвольный элемент трехмерного массива задается как М(i,j,k), где i – номер строки, j – номер столбца, k – номер страницы. Этот элемент можно вывести, а можно присвоить ему определенное значение: М(i,j,k)=4.
Для увеличения размерности массива служит оператор : (двоеточие). Продемонстрируем эту возможность на примере. Пусть у нас задан исходный двухмерный массив М размером 3 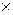 3. Для превращения этого массива в трехмерный к нему добавляются новые страницы так, как показано в следующем m-файле-сценарии. Имеется также возможность удаления отдельной страницы путем присваивания ей пустого массива [].
3. Для превращения этого массива в трехмерный к нему добавляются новые страницы так, как показано в следующем m-файле-сценарии. Имеется также возможность удаления отдельной страницы путем присваивания ей пустого массива [].
%добавление и удаление страниц многомерного массива
M=[1,2,3;4,5,6;7,8,9] % определен двухмерный массив
M(:,:,2)=[10,11,12;13,14,15;16,17,18]; % к двухмерному массиву добавлена
% вторая страница
M
M(:,:,1)=[] % у трехмерного массива удалена первая страница
В результате выполнения этого файла на экран выводится следующее:
M =
1 2 3
4 5 6
7 8 9
M(:,:,1) =
1 2 3
4 5 6
7 8 9
M(:,:,2) =
10 11 12
13 14 15
16 17 18
M =
10 11 12
13 14 15
16 17 18
Путем добавления к массиву M новой 2-й страницы мы получили трехмерный массив размером 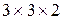 . Затем мы удалили из полученного трехмерного массива первую страницу, в результате чего опять получили двухмерный массив, но состоящий из второй страницы.
. Затем мы удалили из полученного трехмерного массива первую страницу, в результате чего опять получили двухмерный массив, но состоящий из второй страницы.
Из приведенного примера видно, что многомерный массив выводится на экран в виде двухмерных массивов, то есть в виде отдельных страниц.
Для транспонирования многомерных массивов в Matlab имеются функции permute и ipermute. Функция permute ( A , ORDER ) транспонирует  -мерный массив A в соответствии с вектором перестановок ORDER. Элементы вектора перестановок – числа от 1 до
-мерный массив A в соответствии с вектором перестановок ORDER. Элементы вектора перестановок – числа от 1 до  . Функция ipermute ( A , ORDER ) делает то же, но в обратном порядке. Необходимо отметить, что определению (1.2) транспонирования многомерных матриц соответствует функция ipermute. Если ORDER и ORDER1 – две взаимно-обратные перестановки (подстановки), то применение функции permute ( A , ORDER ) и ipermute ( A , ORDER 1) дает один и тот же результат. Последовательное применение B = permute ( A , ORDER ) и С= ipermute ( B , ORDER ) дает результат С=A. Применение этих функций иллюстрируется работой следующего m-файла-сценария.
. Функция ipermute ( A , ORDER ) делает то же, но в обратном порядке. Необходимо отметить, что определению (1.2) транспонирования многомерных матриц соответствует функция ipermute. Если ORDER и ORDER1 – две взаимно-обратные перестановки (подстановки), то применение функции permute ( A , ORDER ) и ipermute ( A , ORDER 1) дает один и тот же результат. Последовательное применение B = permute ( A , ORDER ) и С= ipermute ( B , ORDER ) дает результат С=A. Применение этих функций иллюстрируется работой следующего m-файла-сценария.
% транспонирование многомерной матрицы
M=[1,2,3;4,5,6;7,8,9];
M(:,:,2)=[10,11,12;13,14,15;16,17,18];
M
ORDER=[2,3,1];
ORDER1=[3,1,2]; % перестановка, обратная к ORDER
B=ipermute(M,ORDER)
B1=permute(M,ORDER1)
D=permute(B,ORDER)
В результате выполнения этой программы на экран выводится следующее:
M(:,:,1) =
1 2 3
4 5 6
7 8 9
M(:,:,2) =
10 11 12
13 14 15
16 17 18
B(:,:,1) =
1 4 7
10 13 16
B(:,:,2) =
2 5 8
11 14 17
B(:,:,3) =
3 6 9
12 15 18
B1(:,:,1) =
1 4 7
10 13 16
B1(:,:,2) =
2 5 8
11 14 17
B1(:,:,3) =
3 6 9
12 15 18
D(:,:,1) =
1 2 3
4 5 6
7 8 9
D(:,:,2) =
10 11 12
13 14 15
16 17 18
Мы видим, что массивы M и D равны, равны также массивы B и B1.
Порядок выполнения работы
1.3.1. Сформировать 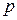 -мерную матрицу
-мерную матрицу 
 -го порядка и
-го порядка и 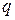 -мерную матрицу
-мерную матрицу 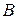
 -го порядка.
-го порядка.
1.3.2. Получить матрицу 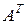 , транспонированную относительно
, транспонированную относительно  соответственно подстановке
соответственно подстановке 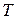 .
.
1.3.3. Получить матрицу 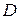 , равную
, равную 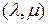 -свернутому произведению матриц
-свернутому произведению матриц  и
и 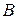 .
.
1.3.4. Сформировать 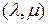 -единичную матрицу
-единичную матрицу 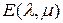
 -го порядка и найти произведение
-го порядка и найти произведение
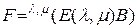 .
.
Указание. Необходимые параметры взять из табл. 1.1 в соответствии с номером варианта задания.
Таблица 1.1
| Номер варианта задания | Размер-ность  матри-цы матри-цы 
| Переста-новка 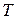
| Размер-ность 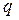 матри-цы матри-цы 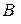
| Порядок 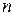 матриц матриц
 и и 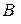
|
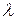
|

|
| 1. | 4 | 4,1,2,3 | 4 | 2 | 0 | 1 |
| 2. | 4 | 3,4,1,2 | 4 | 3 | 0 | 2 |
| 3. | 4 | 2,3,4,1 | 4 | 4 | 0 | 3 |
| 4. | 4 | 1,2,4,3 | 4 | 2 | 0 | 4 |
| 5. | 4 | 2,1,3,4 | 4 | 3 | 1 | 1 |
| 6. | 4 | 2,1,4,3 | 4 | 4 | 1 | 2 |
| 7. | 4 | 1,3,2,4 | 4 | 2 | 1 | 3 |
| 8. | 4 | 4,2,3,1 | 4 | 3 | 2 | 0 |
| 9. | 4 | 3,2,1,4 | 4 | 4 | 2 | 1 |
| 10. | 4 | 1,4,3,2 | 4 | 2 | 2 | 2 |
| 11. | 4 | 3,4,2,1 | 4 | 3 | 3 | 0 |
| 12. | 4 | 4,3,1,2 | 4 | 4 | 3 | 1 |
| 13. | 4 | 3,1,2,4 | 4 | 2 | 4 | 0 |
| 14. | 4 | 1,3,4,2 | 3 | 3 | 0 | 0 |
| 15. | 4 | 1,4,2,3 | 3 | 4 | 0 | 1 |
| 16. | 4 | 4,1,3,2 | 3 | 2 | 0 | 2 |
| 17. | 4 | 2,3,1,4 | 3 | 3 | 0 | 3 |
| 18. | 4 | 2,4,1,3 | 3 | 4 | 1 | 0 |
| 19. | 4 | 2,4,3,1 | 3 | 2 | 1 | 1 |
| 20. | 4 | 3,1,4,2 | 3 | 3 | 1 | 2 |
| 21. | 4 | 3,2,4,1 | 3 | 4 | 1 | 3 |
| 22. | 4 | 4,2,1,3 | 3 | 2 | 2 | 0 |
| 23. | 4 | 4,3,2,1 | 3 | 3 | 2 | 1 |
| 24. | 4 | 4,1,2,3 | 3 | 4 | 3 | 0 |
| 25. | 4 | 1,2,4,3 | 3 | 2 | 3 | 1 |
| 26. | 3 | 1,3,2 | 4 | 3 | 0 | 1 |
| 27. | 3 | 2,1,3 | 4 | 4 | 0 | 2 |
| 28. | 3 | 2,3,1 | 4 | 2 | 0 | 3 |
| 29. | 3 | 3,1,2 | 4 | 3 | 1 | 1 |
| 30 | 3 | 3,2,1 | 4 | 4 | 1 | 2 |
Дата: 2019-02-02, просмотров: 453.