1.2.5.1. Выполнение символьных операций
Для получения разложений аналитических функций в ряд Тейлора можно воспользоваться символьными вычислениями в Matlab. При этом переменные или объекты необходимо объявить символьными с помощью функции syms. Например,
syms x 1 x 2 … создает группу символьных объектов.
syms x 1 x 2 … real и syms x 1 x 2 … unreal создают группы символьных объектов с вещественными (real) и не вещественными (unreal) значениями. Последнюю функцию можно использовать для отмены задания вещественных объектов. Отметим, что символьные переменные здесь разделяются пробелами.
Для получения разложений аналитических функций в ряд Тейлора (1.1) служит функция taylor.
taylor ( f ) – возвращает 6 членов ряда Маклорена.
taylor ( f , n ) – возвращает члены ряда Маклорена до (n-1)-го порядка.
taylor ( f , a ) – возвращает 6 членов ряда Тейлора в окрестности точки a.
taylor ( f , a , n ) – возвращает члены ряда Тейлора до (n-1)-го порядка в окрестности точки a.
Пример 1.7. В результате выполнения программы
clc
clear
syms x t
y1=taylor(exp(-x))
y2=taylor(log(x),6,1)
y3=taylor(sin(x),pi/2,6)
y4=taylor(x^t,3,t)
будет получен следующий результат:
y1 =
1-x+1/2*x^2-1/6*x^3+1/24*x^4-1/120*x^5
y2 =
x-1-1/2*(x-1)^2+1/3*(x-1)^3-1/4*(x-1)^4+1/5*(x-1)^5
y3 =
1-1/2*(x-1/2*pi)^2+1/24*(x-1/2*pi)^4
y4 =
1+log(x)*t+1/2*log(x)^2*t^2
Для вычисления в символьном виде производных от выражения s служит функция diff.
diff ( s ) – возвращает символьное значение первой производной от символьного выражения или массива символьных выражений s по независимой переменной, определенной функцией findsym.
diff ( s , n ) – возвращает символьное значение n-й производной от символьного выражения или массива символьных выражений s по независимой переменной, определенной функцией findsym.
diff ( s ,' v ') или diff ( s , sym (' v ')) – возвращает символьное значение первой производной от символьного выражения или массива символьных выражений s по переменной v.
diff ( s ,' v ', n ) или diff ( s , n ,' v ') – возвращает символьное значение n-й производной от символьного выражения или массива символьных выражений s по переменной v.
Пример 1.8. Программа
clc
clear
syms x t
y1=diff(sin(x^2))
y2=diff(t^6,6)
возвращает следующие результаты:
y1 =
2*cos(x^2)*x
y2 =
720
1.2.5.2. Построение графиков функций одной переменной
Для построения графиков функций одной переменной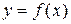 
в Matlab имеется функция plot . График строится в декартовой системе координат по заданным массивам значений аргумента и функции. Заданные этими массивами точки соединяются прямыми линиями. Имеется возможность изменять тип и цвет линии и тип узловых точек (маркер). Вызов этой функции осуществляется командой
plot ( x , y , s )
где x , y – одномерные массивы одинаковой размерности; x – массив значений аргумента функции 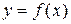; y – массив значений функции 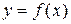; s – строковая константа, определяющая цвет линии, маркер узловых точек и тип линии. Эта константа может содержать от одного до трех символов.
Цвет линии определяется символами y (желтый), m (фиолетовый), c (голубой), r (красный), g (зеленый), b (синий), w (белый), k (черный).
Тип узловой точки определяется символами . (точка), o (окружность), x (крестик), + (плюс), * (звездочка), s (квадрат), d (ромб), < > ^ 
(треугольники различной направленности), p (пятиугольник), h (шестиугольник).
Тип линии определяется символами - (непрерывная), : (короткие штрихи), -. (штрих-пунктир), -- (длинные штрихи).
Символьную константу s можно опустить. В этом случае по умолчанию используется непрерывная линия желтого цвета.
Для построения в одном окне нескольких графиков можно использовать команду
plot(x1,y1,s1,x2,y2,s2,x3,y3,s3,…)
Пример
clc
clear
% графики функций sin x, cos x
x=0:0.1:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,'k-o',x,y2,'r--*')
grid on
В результате выполнения этой программы на экран монитора будет выведено графическое окно с графиками, представленными на рисунке 1.1. Графики представлены в черно-белой палитре, хотя в действительности график функции cos(x) выводится красным цветом.
Команда grid on добавляет на график сетку.
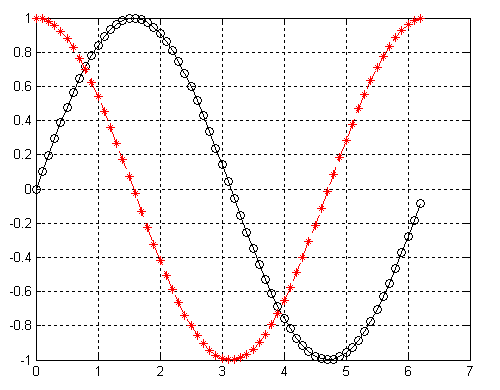
Рис. 1.1. Графики, выполненные с помощью программы plot
Созданный график можно скопировать в буфер Clipboard, активизировав в пункте Edit главного меню окна графики команду Copy Figure, с целью его дальнейшего редактирования в каком-либо графическом редакторе, например Paint.
1.2.5.3. Построение графиков функций двух переменных
Трехмерные поверхности обычно описываются функцией двух переменных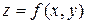 
. Специфика построения трехмерных графиков в Matlab требует не просто задания ряда значений x и y, то есть векторов x и y, а определения двухмерных массивов X и Y. Для создания таких массивов служит функция meshgrid .
[ X , Y ]= meshgrid ( x , y ) – преобразует область, заданную векторами x и y, в двухмерные массивы X и Y, которые могут быть использованы для вычисления значений функции двух переменных и построения трехмерных графиков. Эта функция формирует массивы X и Y таким образом, что строки выходного массива X являются копиями вектора x, а столбцы выходного массива Y – копиями вектора y.
Пример
clc
clear
[X,Y]=meshgrid(1:1:4,6:1:9)
X =
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
Y =
6 6 6 6
7 7 7 7
8 8 8 8
9 9 9 9
В этом примере формируются массивы X и Y для построения трехмерной поверхности при изменении x от 1 до 4 с шагом 1 и y от 6 до 9 с шагом 1.
Командой mesh в Matlab выполняются графики трехмерных поверхностей с заданной или функциональной окраской.
mesh ( X , Y , Z , C ) – выводит в графическое окно сетчатую поверхность с цветами узлов поверхности, заданных массивом С.
mesh ( X , Y , Z ) – аналог предшествующей команды при C = Z, с использованием функциональной окраски, при которой цвет задается высотой поверхности.
Пример
clc
clear
x1=-2:0.1:3;
y1=-4:0.1:4;
[x,y]=meshgrid(x1, y1);
z=x.^2+y.^2;
mesh(x,y,z)
В результате выполнения этой программы на экран будет выведена фигура, приведенная на рисунке 1.4.
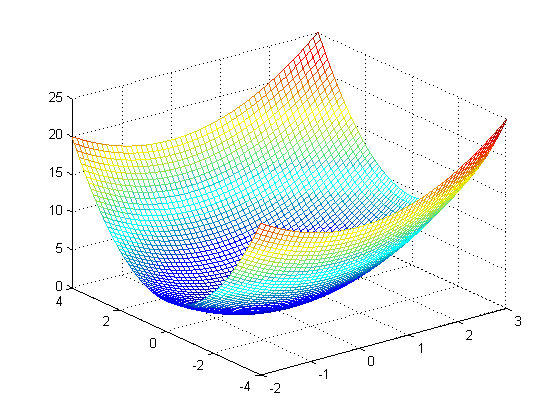
Рис. 1.4. Трехмерный график, построенный с помощью функции mesh
В приведенном примере массив значений функции двух переменных формируется посредством использования поэлементных операций с массивами. Использование поэлементных операций предполагает наличие навыков их использования, т.е. четкого представления того, что происходит при их применении. Если уверенности в правильности использования поэлементных операций нет, то массив значений функции можно сформировать путем использования вложенных циклов for и индексированных переменных. Например, предыдущий пример можно оформить следующим образом:
clc
clear
x1=-2:0.1:3;
y1=-4:0.1:4;
[x,y]=meshgrid(x1,y1);
nx=length(x1);
ny=length(y1);
for i=1:nx
for j=1:ny
z(j,i)=x1(i)^2+y1(j)^2;
end;
end;
mesh(x,y,z)
Заметим, что точке (x1(i),y1(j)) соответствует значение функции z(j,i).
Порядок выполнения работы
1.3.1. Выбрать функцию из таблицы 1.1 в соответствии с номером своего варианта и получить (записать) для нее отрезок ряда Тейлора (1.1) в окрестности некоторой точки до 4-й степени независимой переменной включительно.
1.3.2. Написать m-файл-сценарий для аппроксимации функции одной переменной отрезками ряда Тейлора в окрестности некоторой точки от нулевой до 4-й степени независимой переменной включительно. C помощью программы plot вывести в одно графическое окно графики функции и аппроксимирующих полиномов. Проанализировать точность аппроксимации при различном числе слагаемых ряда Тейлора.
1.3.3. Выбрать функцию из таблицы 1.2 в соответствии с номером своего варианта, представив в ней скалярный аргумент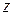 
в виде полинома 1-й или 2-й степени переменных 
, 
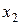, например, в виде
,
,
,
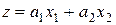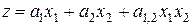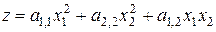и т.д. Для полученной таким образом функции двух переменных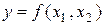 
записать выражение ряда Тейлора (1.2) до 3-й степени независимых переменных включительно.
1.3.4. Написать m-файл-сценарий для аппроксимации функции двух переменных отрезками ряда Тейлора в окрестности некоторой точки от нулевой до 3-й степени независимой векторной переменной включительно. С помощью программы mesh вывести в одно графическое окно графики функции и аппроксимирующих полиномов. Проанализировать точность аппроксимации при различном числе слагаемых ряда Тейлора.
1.3.5. Оформить отчет, в котором привести функцию одной переменной, ее ряд Тейлора до 4-й степени независимой переменной включительно и графическую иллюстрацию аппроксимации, а также функцию двух переменных, ее ряд Тейлора до 3-й степени независимых переменных включительно и графическую иллюстрацию аппроксимации.
Таблица 1.1. Варианты заданий для функций одной переменной
| № вари-анта | Функция | № вари-анта | Функция |
| 1. |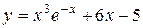 
| 16. |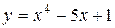 
|
| 2. |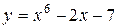 
| 17. | 
|
| 3. | 
| 18. |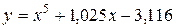 
|
| 4. |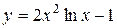 
| 19. |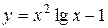 
|
| 5. |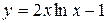 
| 20. |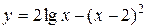 
|
| 6. |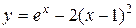 
| 21. |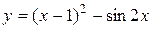 
|
| 7. |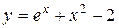 
| 22. |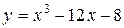 
|
| 8. |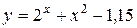 
| 23. |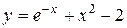 
|
| 9. |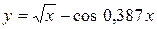 
| 24. | 
|
| 10. |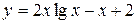 
| 25. |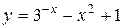 
|
| 11. |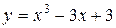 
| 26. |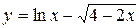 
|
| 12. |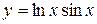 
| 27. |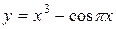 
|
| 13. |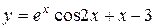 
| 28. |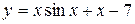 
|
| 14. |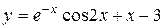 
| 29. |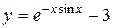 
|
| 15. |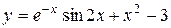 
| 30. |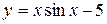 
|
Таблица 1.2. Варианты заданий для функций двух переменных
| № вари-анта | Функция | № вари-анта | Функция |
| 1. |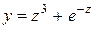 
| 16. |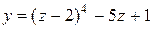 
|
| 2. |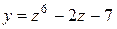 
| 17. |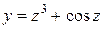 
|
| 3. |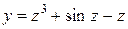 
| 18. |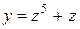 
|
| 4. |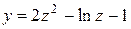 
| 19. |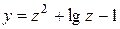 
|
| 5. |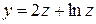 
| 20. |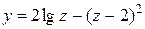 
|
| 6. |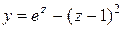 
| 21. |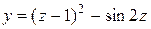 
|
| 7. |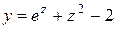 
| 22. |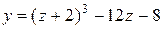 
|
| 8. |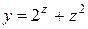 
| 23. |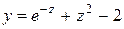 
|
| 9. |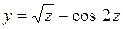 
| 24. |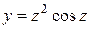 
|
| 10. |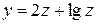 
| 25. |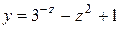 
|
| 11. |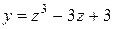 
| 26. | 
|
| 12. |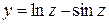 
| 27. |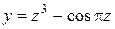 
|
| 13. |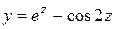 
| 28. |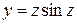 
|
| 14. |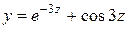 
| 29. |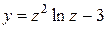 
|
| 15. |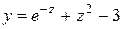 
| 30. |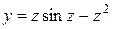 
|
Дата: 2019-02-02, просмотров: 468.
