Приведенные рекомендации были положены в основу создания MOLAP-системы для аналитической обработки метеорологических данных.
В настоящее время метеорологические данные доступны в виде отдельных таблиц с данными, как это имеет место, например, в http://gismeteo.ru или http://pogoda.by. Имеющиеся таблицы с данными относятся к определенной метеостанции. Это затрудняет выполнение параллельной обработки данных, т.е. одновременной обработки данных ряда метеостанций. Кроме того, данные обычно относятся к фиксированному интервалу времени (году, месяцу). Это затрудняет обработку данных за произвольные интервалы времени. Указанных недостатков лишена многомерная модель метеорологических данных.
Структура файла осей многомерной модели метеорологических данных представлена в таблице 1.
Таблица 1. Структура файла осей многомерной модели
метеорологических данных
| Наименование оси | Метеостанция | Год | Месяц | День | Час |
| Номер оси | Ось 1 | Ось 2 | Ось 3 | Ось 4 | Ось 5 |
| Позиция в файле | 1 | 2 | 3 | 4 | 5 |
Таким образом, в качестве осей многомерной модели метеорологических данных нами выбраны метеостанция, год, месяц, день, час, так как они однозначно определяют данные. Файл осей данных выглядит следующим образом:
Метеостанция,26850,…,26666,
Год,1998,1999,…,2009,
Месяц,1,2,3,4,5,6,7,8,9,10,11,12,
День,1,2,3,…31,
Час,0,3,6,9,12,15,18,21,
Метеостанции определяются принятым во Всемирной метеорологической организации (ВМО) кодом. Так, 26850 – это Минск, 26666 – Витебск. Метеорологические данные собираются с периодичностью в 3 часа, начиная с 0 часов (по Гринвичу), что отражено в оси "Час".
Структура файла данных многомерной модели метеорологических данных (многомерной базы данных) представлена в таблице 2.
Таблица 2. Структура файла данных многомерной модели
метеорологических данных
| Данные | Позиция в файле |
| Скалярное значение мультииндекса | 1 |
| Температура воздуха | 2 |
| Атмосферное давление на уровне моря | 3 |
| Направление ветра | 4 |
| Скорость ветра | 5 |
| Относительная влажность воздуха | 6 |
| Количество облаков | 7 |
| Атмосферное давление на уровне станции | 8 |
| Величина барической тенденции | 9 |
| Атмосферное давление на уровне моря | 10 |
| Величина барической тенденции | 11 |
Строки файла данных (на примере двух строк) выглядят следующим образом:
1,0,0,0,0,0,0,0,0
17266,18.5,1016.7,40,4,40.3,9999,9999,0.5
Первая строка со скалярным значением мультииндекса 1 (ему соответствует векторное значение мультииндекса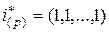 
), соответствует началу координат и указывает на наименования осей. По определению эта строка не содержит данных, поэтому они обозначены как нулевые. Значение 9999 означает, что данные отсутствуют. В частности, во второй строке отсутствуют данные о количестве облаков и атмосферном давлении на уровне моря.
Описанная многомерная модель метеорологических данных была реализована в виде программного средства на кафедре ИТАС. Импорт данных в многомерную модель организован из текстовых файлов, структура которых приведена в таблице 3.
Таблица 3. Структура файла данных для импорта в многомерную базу данных
| Данные | Позиция в файле |
| Номер (код) метеостанции | 1 |
| Дата наблюдения | 2 |
| Срок наблюдения | 3 |
| Форма (количество) облаков | 4 |
| Направление ветра | 5 |
| Скорость ветра | 6 |
| Температура | 7 |
| Относительная влажность | 8 |
| Атмосферное давление на уровне станции | 9 |
| Атмосферное давление на уровне моря | 10 |
| Величина барической тенденции | 11 |
Были реализованы также такие процедуры, как изменение длин осей, удаление данных, формирование текстовых отчетов, вращение, просмотр осей.
ЛИТЕРАТУРА
1. Альперович М. Введение в OLAP и многомерные базы данных. http://www.cfin.ru/itm/olap/intro.shtml?printversion
2. Амосов А.А., Колпаков В.В. Скалярно-матричное дифференцирование и его приложения к конструктивным задачам теории связи // Проблемы передачи информации. – 1972. – №. 8. – Вып. 1. – С. 3–15.
3. Аоки М. Оптимизация стохастических систем. – М.: Наука, 1971. – 424 с.
4. Баландин Ю.П., Милов Л.Т. Метод наименьших квадратов для многомерных массивов данных // Управление. Передача, преобразование и отображение информации / Межвузовский сб. статей. – Рязань, 1977. – Вып. 4. – С. 11–17.
5. Бейтмен Г., Эрдейи А. Высшие трансцендентные функции: Гипергеометрическая функция, функция Лежандра. – М.: Наука, 1973. – 294 с.
6. Бейтмен Г., Эрдейи А. Высшие трансцендентные функции: Функции Бесселя, функции параболического цилиндра, ортогональные многочлены. – М.: Наука, 1974. – 295 с.
7. Беллман Р. Введение в теорию матриц. – М.: Наука, 1969. – 368 с.
8. Боровков А.А. Теория вероятностей. – М.: Наука, 1986. – 432 с.
9. Браммер К., Зиффлинг Г. Фильтр Калмана-Бьюси. – М.: Наука, 1982. – 200 с.
10.Гайшун И.В. Вполне разрешимые многомерные дифференциальные уравнения. – Мн.: Наука и техника, 1983. – 272 с.
11.Гайшун И.В. Линейные уравнения в полных производных. – Мн.: Наука и техника, 1989. – 254 с.
12.Гантмахер Ф.Р. Теория матриц. – М.: Наука, 1988. – 552 с.
13.Гендель Е.Г., Мунерман В.И. Применение алгебраических моделей для синтеза процессов обработки файлов // Управляющие системы и машины. – 1984. – № 4. – С. 69–72.
14.Гурса Э. Курс математического анализа. – М.–Л.: ОНТИ, 1936. – Т. 1. –592 с.
15.Данилов Д.Л., Жиглявский А.А. Главные компоненты временных рядов: Метод "гусеница". – 1997.
16.Де Гроот М. Оптимальные статистические решения. – М.: Мир,1974. – 496 с.
17.Джайн А.К. Успехи в области математических моделей для обработки изображений // ТИИЭР. – 1981. – Т. 69. – № 5. – С. 9–39.
18.Дьедонне Ж. Основы современного анализа. – М.: Мир, 1964. – 432 с.
19.Ермаков С.М., Жиглявский А.А. Математическая теория оптимального эксперимента. – М.: Наука, 1987. – 320 с.
20.Икрамов Х.Д. Численные методы линейной алгебры. – М.: Знание, 1987. – 47 с.
21.Казаков И.Е. Обобщение метода статистической линеаризации на многомерные системы // Автоматика и телемеханика. – 1965. – Т. 26. – № 7. – С. 1210–1215.
22.Калиткин Н.Н. Численные методы. – М.: Наука, 1978. – 512 с.
23.Колло Д. Матричная производная для статистики. – Тарту: 1991. – 155 с.
24.Калужнин Л.А., Сущанский В.И. Преобразования и перестановки. – М.: Наука, 1979. – 112 с.
25.Картан А. Дифференциальное исчисление и дифференциальные формы. – М.: Мир, 1971. – 392 с.
26.Кендалл М., Стьюарт А. Теория распределений. – М.: Наука, 1966. – 587 с.
27.Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. – М.: Наука, 1972. – 496 с.
28.Колмогоров А.Н. Интерполирование и экстраполирование стационарных случайных последовательностей // Известия АН СССР. Сер. математическая. – 1941. – Т. 5.– С. 3–14.
29.Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. – М.: МЦНМО, 2001. – 960 с.
30.Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. – М.: Наука, 1973. – 832 с.
31.Крамер Г. Математические методы статистики. – М.: Мир, 1975. – 648 с.
32.Кудрявцев Л.Д. Курс математического анализа. – М.: Высш. школа, 1981. – Т.2. – 584 с.
33.Левин Б.Р. Теоретические основы статистической радиотехники. Книга первая. – М.:Сов. радио, 1969. – 752 с.
34.Ли Р. Оптимальные оценки, определение характеристик и управление. – М.: Наука, 1966. – 176 с.
35.Лурье К.А. Оптимальное управление в задачах математической физики. – М.: Наука, 1975. – 478 с.
36.Мак-Кракен Д., Дорн У. Численные методы и программирование на Фортране. – М.: Мир, 1977. – 584 с.
37.Маркус М., Минк Х. Обзор по теории матриц и матричных неравенств. – М.: Наука, 1972. – 232 с.
38.Медич Дж. Статистически оптимальные линейные оценки и управление. – М.: Энергия, 1973. – 440 с.
39.Милов Л.Т. Многомерные матрицы при обработке массивов данных // Управление. Передача, преобразование и отображение информации / Межвузовский сб. статей. – Рязань, 1977. – Вып. 4. – С. 3–11.
40.Милов Л.Т. Многомерно-матричные производные и анализ чувствительности систем автоматического управления // Автоматика и телемеханика. – 1979. – № 9. – С. 15–25.
41.Митенков В.Б., Конычев В.И., Емельченко Е.П., Мунерман В.И., Самойлов М.Ю., Самойлова Т.А. // Эффективное решение задач обработки результатов летных испытаний на суперкомпьютерах // Тезисы докладов международной конференции "Авиационные технологии 2000". – Жуковский, 1997. – С. 15–16.
42.Монин А.С., Яглом А.М. Статистическая гидромеханика. Часть 1. – М.: Наука, 1965. – 639 с.
43.Мунерман В.И. Принципы создания многомерных аналитических информационных систем // Программа IV ежегодной научно-практической конференции "Создание единого информационного пространства Смоленской области" (25 апреля 2002 года) http://admin.smolensk.ru/sobyt/konfer/progr.htm
44.Мунерман В.И. Параллельная обработка данных. Методы и средства http://www.smolensk.ru/user/sgma/MMORPH/N-3-html/23.htm
45.Муха В.С. Нерекуррентный фильтр для гауссовских процессов // Автоматика и вычислительная техника. – 1985. – Вып.14. – C. 47–50.
46.Муха В.С. Многомерно-матричные производные и разложение функции нескольких переменных в ряд Тейлора // Автоматика и вычислительная техника. – 1987. – Вып. 16. – С. 65–71.
47.Муха В.С. Многомерно-матричные полиномы Эрмита // Известия АНБ. Сер. физ.-мат. наук. – 1990. – № 4. – С. 42–47.
48.Муха В.С. Многомерно-матричные дифференциальные уравнения и анализ чувствительности систем // Автоматика и вычислительная техника. – 1991. – Вып. 20. – С. 128–133.
49.Муха В.С. Многомерно-матричный подход к оцениванию реализаций векторных нестационарных процессов // Доклады 12 научно-технического семинара "Статистический синтез и анализ информационных систем" (23–25 июня 1992 г., г. Черкассы). – Москва-Черкассы, 1992. – С. 137–139.
50.Муха В.С. О многомерно-матричных дифференциальных уравнениях // Весцi АНБ. Сер. фiз.-мат. навук. – 1993. – № 2. – С. 37–44.
51.Муха В.С. Формальные правила транспонирования многомерных матриц // Автоматика и вычислительная техника. – 1993. – Вып. 21. – С. 65–72.
52.Муха В.С. К аппроксимации многомерных зависимостей и распределений рядами по полиномам Эрмита // Применение многомерного статистического анализа в экономике и оценке качества продукции: Тез. докл. 5-й науч. конф. стран СНГ. – М.: ЦЭМИ РАН, 1993. – С. 77–78.
53.Муха В.С. Ряды Фурье и Грама-Шарлье по многомерно-матричным полиномам Эрмита // Современные проблемы компьютерного анализа данных и моделирования: Сб. науч. ст. – Мн.: Белгосуниверситет, 1993. – С. 64–69.
54.Муха В.С. Расчет моментов многомерного гауссовского распределения // Весцi АНБ. Сер. фiз.-мат. навук. – 1993. – № 4. – С. 39–43.
55.Муха В.С. К теории полиномов Эрмита одной переменной и их применению // Автоматика и вычислительная техника. – Вып. 22.– Мн.,1994. – С. 58–63.
56.Муха В.С. Расчет моментов распределения Уишарта // Компьютерный анализ данных и моделирование: Сб. науч. ст. междунар. конф. (Минск, 4–8 сент. 1995 г.). – Т. 2. – Мн.: Белгосуниверситет, 1995. – С. 207–212.
57.Муха В.С. Дифференцирование функций симметричных матриц // Весцi АНБ. Сер. фiз.-мат. навук. – 1997. – № 2. – С. 46–53.
58.Муха В.С. К теории полиномов Лягерра векторной переменной // Еругинские чтения-IV: Тез. докл. междунар. матем. конф. (Витебск, 20–22 мая 1997 г.). – Витебск: Изд.-во Витебского госуниверситета, 1997. – С. 158–159.
59.Муха В.С. Многомерно-матричная технология для полиномов Лягерра векторной переменной в вероятностных приложениях // Электромагнитные волны и электронные системы. – 1998. – Т 3. – №4 . – С. 18–22.
60.Муха В.С. Многомерно-матричная технология в теории моделирования изображений // Материалы международной научно-технической конференции "Новые информационные технологии в науке и производстве".–Мн.:БГУИР,1998. – С. 199–202.
61.Муха В.С. Моделирование многомерных систем и процессов. Многомерно-матричный подход: Методическое пособие для аспирантов и научных работников. – Мн.: БГУИР, 1998. – 40 с.
62.Муха В.С. Многомерно-матричный подход к теории ортогональных систем полиномов векторной переменной // Тезисы докладов международной математической конференции "Еругинские чтения VI". (Гомель, 20–21 мая 1999 г.). – Часть 1. – Гомель: ГГУ им. Ф. Скорины, 1999. – C. 159–160.
63.Муха В.С. Байесовская фильтрация случайных полей и изображений // Вторая международная конференция "Цифровая обработка информации и управление в чрезвычайных ситуациях" (Минск, 28–30 ноября 2000 г.). Доклады. – Т. 1. – Мн., 2000. – С. 19 – 24.
64.Муха В.С. Многомерно-матричный подход к теории ортогональных систем полиномов векторной переменной // Весцi НАН Беларусi. Сер. фiз.-мат. навук.– 2001. – № 2. – С. 64–68.
65.Муха В.С. Статистическое распознавание многомерных негауссовских образов // Автоматика и телемеханика. – 2001. – № 4. – С. 80–90.
66.Муха В.С. Теория вероятностей: Учебное пособие для студентов технических специальностей высших учебных заведений. – Мн.: БГУИР, 2001. – 168 с.
67.Мысовских И.П. Интерполяционные кубатурные формулы. – М.: Наука, 1981. – 336 с.
68.Никифоров А.Ф., Уваров В.Б. Специальные функции математической физики. – М.: Наука, 1984. – 344 с.
69.Обухов А.М. Статистическое описание непрерывных полей // Труды геофизического института АН СССР. – 1954. – Вып. 24 (151). – С. 3–42.
70.Острем К.Ю. Введение в стохастическую теорию управления. – М.: Мир, 1973. – 322 с.
71.Принципы проектирования и использования многомерных баз данных (WinWord) http://students.informika.ru/essay/Detailed/1744.html
72.Прэтт У. Цифровая обработка изображений. – Кн. 1. – М.: Мир,1982. – 312 с.
73.Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. Элементарные функции. – М.: Наука, 1981. – 800 с.
74.Пугачев В.С., Синицын И.Н. Стохастические дифференциальные системы. Анализ и фильтрация. – М.: Наука, 1990. – 632 с.
75.Рамм А.Г. Теория оценивания случайных полей. – М.: Мир, 1996. – 352 с.
76.Рао С.Р. Линейные статистические методы и их применение. – М.: 1968. – 548 с.
77.Рудин У. Основы математического анализа. – М.: Мир, 1976. – 319 с.
78.Сегё Г. Ортогональные многочлены. – М.: Физматгиз, 1962.
79.Синицын И.Н. Методы статистической линеаризации (обзор) // Автоматика и телемеханика. – 1974. – № 5. – С. 82–94.
80.Сираждинов С.Х. К теории многомерных полиномов Эрмита // Труды института математики и механики АН Уз. ССР. – 1949. – Вып. 5. – С. 70–95.
81.Соколов Н.П. Введение в теорию многомерных матриц. – Киев: Наукова думка, 1972. – 176 с.
82.Соколов Н.П. Пространственные матрицы и их приложения. – М.: Физматгиз, 1960. – 300 с.
83.Соколов Н.П. Об операциях над многомерными матрицами // Доклады АН СССР. – 1965. – Т. 163. – № 6. – С. 1322–1325.
84.Соколов Н.П. О функциях от многомерных матриц и применении их к решению линейных систем дифференциальных уравнений в частных производных // Укр. матем. журнал. – 1970. – Т. 22. – № 6. – С. 762–768.
85.Стрейц В. Методы пространства состояний в теории дискретных линейных систем управления. – М.: Наука, 1985. – 296 с.
86.Суетин П.К. Классические ортогональные многочлены. – М.: Наука, 1979. – 415 с.
87.Суетин П.К. Ортогональные многочлены по двум переменным. – М.: Наука, 1988. – 384 с.
88.Сю Д., Мейер А. Современная теория автоматического управления и ее применения. – М.: Машиностроение, 1972. – 552 с.
89.Тихонов В.И., Миронов М.А. Марковские процессы. – М.: Сов. радио, 1977. – 488 с.
90.Толстов Г.П. Курс математического анализа. – М.: Гос. изд. ТТЛ, 1957. – Т. 2. – 544 с.
91.Ту Ю. Современная теория управления. – М.:Машиностроение,1971. – 472 с.
92.Уилкс С. Математическая статистика. – М.: Наука, 1967. – 632 с.
93.Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. – М.-Л.: Физматгиз, 1963. – 734 с.
94.Феденя О.А. Многомерные матрицы и некоторые экстремальные комбинаторные задачи: Дис.-я на соиск. уч. ст. к. ф.-м. наук. – Ин-т матем. АН БССР. – 1978. – 103 с.
95.Фомин Я.А., Тарловский Г.Р. Статистическая теория распознавания образов. – М.: Радио и связь, 1986. – 264 с.
96.Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений. – М.: Мир, 1980. – 280 с.
97.Хабиби А. Двумерная байесовская оценка изображений // ТИИЭР. – 1971. – Т. 60. – № 7. – С. 153–159.
98.Халмош П. Конечномерные векторные пространства. – М.:ФМ,1963. – 264 с.
99.Харин Ю.С. Робастность в статистическом распознавании образов. – Мн.: Университетское, 1985. – 232 с.
100. Харин Ю.С., Степанова М.Д. Практикум на ЭВМ по математической статистике. – Мн.: Университетское, 1987. – 304 с.
101. Хорн Р., Джонсон Ч. Матричный анализ. – М.: Мир, 1989. – 656 с.
102. Чукин Ю.В. Структуры данных для представления изображений // Зарубежная радиоэлектроника. – 1983. – № 8. – С. 87–103.
103. Шварц Л. Анализ. – Т . 1. – М.: Мир, 1972. – 824 с.
104. Шеффе Г. Дисперсионный анализ. – М.: Наука, 1980. – 512 с.
105. Шмелев А.Б. Основы марковской теории нелинейной обработки случайных полей. – М.: МФТИ, 1998. – 208 с.
106. Яншин В.В. Многосвязные цепи Маркова как пространственные матрицы // Доклады АН СССР. – 1991. – Т. 318. – № 5. – С. 1108–1112.
107. Appel P., Kampe de Feriet. Fonctions hypergeometriques et hyperspheriques. Polynomes D'Hermite. – Paris, 1926. – 390 p.
108. Bhatia R. Matrix Analysis. – Mew Dehli: Springer, 1997. – 347 p.
109. Brewer J.W. The derivative of the exponential matrix with respect to a matrix // IEEE Trans. – 1970. – V. AC-15. – № 2. – P. 241–244.
110. Brookes D.M. The Matrix Reference Manual. Section Matrix Calculus. – Imperial College of science, technology and medicine, London. http://www.cs.uwaterloo.ca/~frey/matrix/calculus.html
111. Dwyer P.S., Macphail M.S. Symbolic matrix derivatives // Annals of mathem. statistics. – 1948. – V. 19. – № 4. – P. 517–534.
112. Fraser R.A., Duncan W.Y., Collar A.R. Elementary matrices and some applications to dynamics and differential equations. – Cambridge university press, 1936.
113. Hermite M. Sur un nouveau doveloppement en serie des fonctions // Comptes Rendus hebdomadaires des seances de l'Academie des sciences. – 1864. – V. 58. – P. 93–100, 266–273.
114. Isserlis L. On a formula for the product-moment coefficient of any order of a normal frequency distribution in any number of variables // Biometrika. – 1918. – 12, № 1–2, – P. 134–139.
115. Kalman R.E. A new approach to linear filtering and prediction problems // Trans. ASME, series D. Journal of basic engineering. – March, 1960. – P. 35–45.
116. Krattenthaler C., Schlosser M. A new multidimensional matrix inverse with applications to multiple q-series // Discrete Mathematics. – 1999. – 204 . – P. 249–279.
117. MacRae E.C. Matrix derivatives with an application to adaptive linear decision problem // An. Statist. – 1974. – № 2. – P. 337–346.
118. Mukha V., Burtsev A. An Approach to the Multivariate Non-Gaussian Patterns Statistical Recognition // Computer Data Analysis and Modelling / Proceeding of the fifth Internationale Conference (Juni 8–12, 1998, Minsk, Republic of Belarus).– Minsk:BSU,1998. – P. 17–22.
119. Mukha V., Batin N. Statistical Recognition of Multivariate Essentially Non-Gaussian Patterns // Proceeding of Fifth International Conference PRIP'99 "Pattern Recognition and Information Processing" (May 18–20, 1999, Minsk, Republic of Belarus). – V. 1. – Minsk-Szczecin, 1999. – P. 163–167.
120. Mukha V.S. Statistical Recognition of Multivariate Non-Gaussian Patterns // Automation and Remote Control. – 2001. – V. 62. – № 4. – P. 580–590.
121. Neudecker H. Some theorems on matrix differentiations with special reference to Kronecker matrix products // J. Amer. Statist. Assoc. – 1969. – № 64. – P. 953–963.
122. Ramm A.G. Random Fields Estimation Theory. – New York: London Scientifik and Wiley, 1990.
123. Sebastiani P. On the Derivatives of Matrix Powers // SIAM Journal on Matrix Analysis and Applications. – V. 17(3). – July 1996. – P. 640–648.
124. Vetter W.J. Derivative operations on matrices // IEEE Trans. – 1970. – V. AC-15. – № 2. – P. 241–244.
Анализ многомерных данных
Практический раздел
Индивидуальные практические занятия для студентов специальности
1-53 01 02 "Автоматизированные системы обработки информации"
дистанционной формы обучения
Указания к выбору варианта
Выполните индивидуальные практические занятия по двум темам. Варианты возьмите из таблицы 1.0 в соответствии с последними двумя цифрами номера зачетки, отделенными дефисом. Если номер зачетки не содержит таких двух цифр, то обратитесь за вариантом к преподавателю. Отчет по каждой теме пришлите в виде отдельной папки, содержащей программы (m -файлы), отвечающие на каждый пункт "порядка выполнения работы". Имена файлов должны содержать номер пункта задания, например, файл с именем prog2_3_1.m решает задачи пункта 2.3.1 задания по теме 2. Если работа не зачтена, т.е. по ней имеются замечания, то присылайте работу целиком, включая и зачтенные вопросы (новую папку). Старая папка будет заменена новой и выполнена проверка.
Таблица 1.0
Номера вариантов индивидуальных практических занятий
| Две последние цифры зачетки | Вариант темы 1 по таблице 1.1 | Вариант темы 2 по таблице 1.2 |
| [ 1] | '1.03' | '2.18' |
| [ 2] | '1.30' | '2.05' |
| [ 3] | '1.13' | '2.11' |
| [ 4] | '1.19' | '2.07' |
| [ 5] | '1.01' | '2.12' |
| [ 6] | '1.16' | '2.03' |
| [ 7] | '1.21' | '2.02' |
| [ 8] | '1.08' | '2.03' |
| [ 9] | '1.25' | '2.09' |
| [ 10] | '1.02' | '2.25' |
| [ 11] | '1.22' | '2.14' |
| [ 12] | '1.03' | '2.23' |
| [ 13] | '1.25' | '2.22' |
| [ 14] | '1.27' | '2.01' |
| [ 15] | '1.21' | '2.26' |
| [ 16] | '1.28' | '2.08' |
| [ 17] | '1.04' | '2.20' |
| [ 18] | '1.26' | '2.27' |
| [ 19] | '1.08' | '2.18' |
| [ 20] | '1.26' | '2.03' |
| [ 21] | '1.29' | '2.08' |
| [ 22] | '1.17' | '2.30' |
| [ 23] | '1.26' | '2.18' |
| [ 24] | '1.01' | '2.08' |
| [ 25] | '1.22' | '2.25' |
| [ 26] | '1.19' | '2.19' |
| [ 27] | '1.11' | '2.16' |
| [ 28] | '1.27' | '2.21' |
| [ 29] | '1.01' | '2.27' |
| [ 30] | '1.21' | '2.04' |
| [ 31] | '1.17' | '2.01' |
| [ 32] | '1.17' | '2.15' |
| [ 33] | '1.13' | '2.05' |
| [ 34] | '1.18' | '2.02' |
| [ 35] | '1.29' | '2.04' |
| [ 36] | '1.19' | '2.24' |
| [ 37] | '1.02' | '2.20' |
| [ 38] | '1.22' | '2.20' |
| [ 39] | '1.10' | '2.10' |
| [ 40] | '1.04' | '2.26' |
| [ 41] | '1.19' | '2.09' |
| [ 42] | '1.16' | '2.23' |
| [ 43] | '1.03' | '2.09' |
| [ 44] | '1.10' | '2.29' |
| [ 45] | '1.11' | '2.29' |
| [ 46] | '1.21' | '2.12' |
| [ 47] | '1.22' | '2.21' |
| [ 48] | '1.16' | '2.01' |
| [ 49] | '1.26' | '2.26' |
| [ 50] | '1.26' | '2.22' |
| [ 51] | '1.08' | '2.01' |
| [ 52] | '1.08' | '2.29' |
| [ 53] | '1.03' | '2.19' |
| [ 54] | '1.29' | '2.06' |
| [ 55] | '1.11' | '2.21' |
| [ 56] | '1.13' | '2.13' |
| [ 57] | '1.03' | '2.26' |
| [ 58] | '1.22' | '2.13' |
| [ 59] | '1.30' | '2.21' |
| [ 60] | '1.29' | '2.20' |
| [ 61] | '1.26' | '2.10' |
| [ 62] | '1.11' | '2.29' |
| [ 63] | '1.11' | '2.21' |
| [ 64] | '1.02' | '2.22' |
| [ 65] | '1.27' | '2.26' |
| [ 66] | '1.19' | '2.16' |
| [ 67] | '1.01' | '2.15' |
| [ 68] | '1.04' | '2.02' |
| [ 69] | '1.11' | '2.1' |
| [ 70] | '1.30' | '2.25' |
| [ 71] | '1.23' | '2.03' |
| [ 72] | '1.22' | '2.01' |
| [ 73] | '1.03' | '2.18' |
| [ 74] | '1.12' | '2.13' |
| [ 75] | '1.02' | '2.07' |
| [ 76] | '1.02' | '2.09' |
| [ 77] | '1.05' | '2.01' |
| [ 78] | '1.18' | '2.24' |
| [ 79] | '1.10' | '2.17' |
| [ 80] | '1.19' | '2.15' |
| [ 81] | '1.25' | '2.03' |
| [ 82] | '1.17' | '2.01' |
| [ 83] | '1.30' | '2.10' |
| [ 84] | '1.29' | '2.20' |
| [ 85] | '1.11' | '2.13' |
| [ 86] | '1.17' | '2.09' |
| [ 87] | '1.23' | '2.24' |
| [ 88] | '1.30' | '2.20' |
| [ 89] | '1.13' | '2.11' |
| [ 90] | '1.13' | '2.13' |
| [ 91] | '1.10' | '2.26' |
| [ 92] | '1.09' | '2.21' |
| [ 93] | '1.03' | '2.30' |
| [ 94] | '1.13' | '2.12' |
| [ 95] | '1.10' | '2.14' |
| [ 96] | '1.12' | '2.17' |
| [ 97] | '1.24' | '2.18' |
| [ 98] | '1.18' | '2.25' |
| [ 99] | '1.29' | '2.21' |
Дата: 2019-02-02, просмотров: 472.
