(относительного вращающего момента)
Расчёт приведённого плеча mк деформирующей силы и построение графика m K= m K(α) можно выполнять в прикладной программе обработки электронных таблиц «MS Excel». Расчёт ведём в следующей последовательности (рис. 4.4):
1. На рабочем листе Excel столбцам A, B, C, D, E, F, G, H, и I присваиваем имена, например, «αgrad», «αrad», «d0», «dА», «dВ», «d1», «mα», «mf» и «mк» соответственно. Имена заносим в ячейки А1 – I1.
2. В ячейки А2–А11 заносим углы поворота кривошипа от 0 до 90º с шагом 10º. Формат ячеек – числовой, число десятичных знаков – 0.
3. В ячейку В2 вносим стандартную функцию «РАДИАНЫ» для перевода градусной меры измерения углов в радианную. После определения значения угла в этой ячейки определяем значения углов в остальных ячейках В3–В11. Формат ячеек – числовой, число десятичных знаков – 5.
4. Во все ячейки С2-C11 заносим найденное значение d0. Размерность d0 – метры (м). Формат ячеек столбца С и всех остальных столбцов от D до I включительно – числовой, число десятичных знаков – 3.
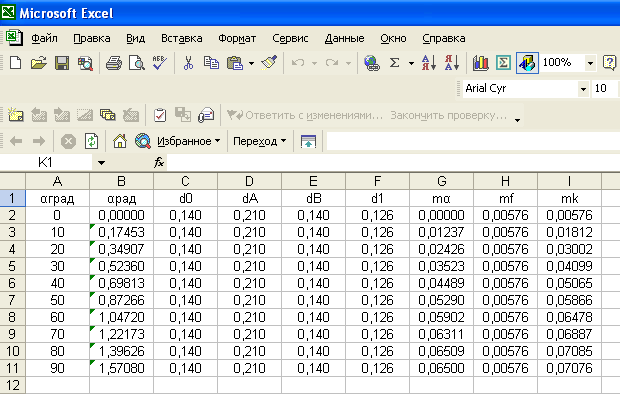
Рис. 4.4 Расчёт приведённого плеча деформирующей силы mK MS Excel
5. В ячейку D2 в соответствие с формулой d A=1,5d0 записываем формулу для определения диаметра d A. Диаметр d A рассчитываем в (м). После определения значения d A в этой ячейке определяем значения d A в остальных ячейках D3–D11.
6. В ячейку Е2 в соответствие с формулой d В=d0 записываем формулу для определения диаметра dВ. Диаметр d В рассчитываем в (м.) После определения значения d В в этой ячейке определяем значения d В в остальных ячейках Е3–Е11.
7. В ячейку F2 в соответствие с формулой d1=0,9d0 записываем формулу для определения диаметра d1. Диаметр d1 рассчитываем в (м). После определения значения d1 в этой ячейке определяем значения d1 в остальных ячейках F3–F11.
6. В ячейку G2 в соответствие с формулой (2.7) записываем формулу для расчёта приведённого идеального плеча силы 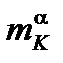 . Величину
. Величину 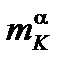 рассчитываем в (м). После определения значения
рассчитываем в (м). После определения значения 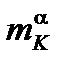 в этой ячейке определяем значения
в этой ячейке определяем значения 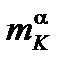 в остальных ячейках G3–G11.
в остальных ячейках G3–G11.
7. В ячейку Н2 в соответствие с формулой (2.8) записываем формулу для расчёта приведённого плеча силы трения  . Величину
. Величину 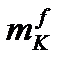 рассчитываем в (м). После определения значения
рассчитываем в (м). После определения значения 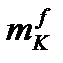 в этой ячейке определяем значения
в этой ячейке определяем значения  в остальных ячейках Н3–Н11.
в остальных ячейках Н3–Н11.
8. В ячейку I2 в соответствие с формулой (2.6) записываем формулу для расчёта приведённого плеча деформирующей силы 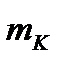 . Величину
. Величину 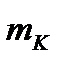 рассчитываем в (м). После определения значения
рассчитываем в (м). После определения значения 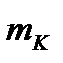 в этой ячейке определяем значения
в этой ячейке определяем значения 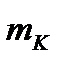 в остальных ячейках I3–I11. По найденным значениям
в остальных ячейках I3–I11. По найденным значениям 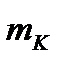 строим график зависимости
строим график зависимости 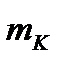 =
= 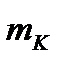 (α) (рис. 4.5).
(α) (рис. 4.5).
Рис. 4.5 График зависимости mK= mK(α)
Проверочный расчёт вала
Деформирующую силу Р D на ползуне, допускаемую прочностью главного вала, определяем по следующей формуле, которая соответствует выбранной нами расчётной схеме:
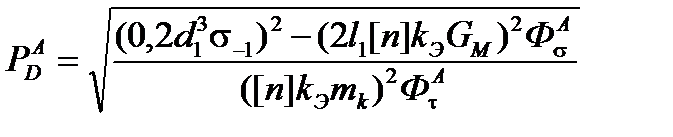 (4.1)
(4.1)
Индекс «А» в обозначениях величин 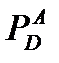 ,
, 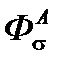 и
и 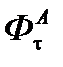 указывает на то, что расчёт вала ведется по сечению «А-А», которое является наиболее опасным.
указывает на то, что расчёт вала ведется по сечению «А-А», которое является наиболее опасным.
Для уменьшения вероятности внесения ошибок в расчётную программу при записи этой формулы, её целесообразно разбить на несколько простых комплексов, которые в программу будут записываться по отдельности. Например, формулу (4.1) можно представить в виде:
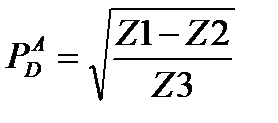 , (4.2)
, (4.2)
где Z1, Z2 и Z3 – следующие комплексы:
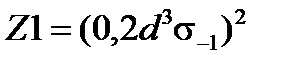 (4.3)
(4.3)
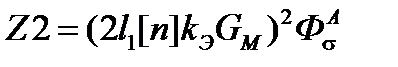 (4.4)
(4.4)
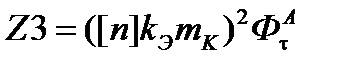 (4.5)
(4.5)
Исходные данные для расчёта:
σ–1 =235 МПа = 235·106 Па (н/м2) (см. с. 64)
[n]=1,3 (см. табл. 2.5);
kЭ = 0,8 (см. табл. 2.6);
r =11 мм =0,011 м (см. с. 64);
d1=125 мм =0,125 м (см. с. 63);
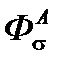 =2,0 (рис. 2.13 а: d=d1=125 мм, r/d = r/d1=0,087);
=2,0 (рис. 2.13 а: d=d1=125 мм, r/d = r/d1=0,087);
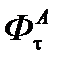 =3,2 (рис. 2.13 б: d=d1=125 мм, r/d = r/d1=0,087);
=3,2 (рис. 2.13 б: d=d1=125 мм, r/d = r/d1=0,087);
G М – вес муфты с зубчатым колесом:
G М = G З K + G МС, (4.6)
где G З K – вес зубчатого колеса;
G МС – вес муфты сцепления.
Вес зубчатого колеса равен:
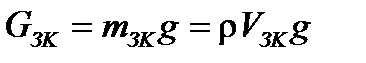 , (4.7)
, (4.7)
где mзк – масса зубчатого колеса, кг;
g – ускорение свободного падения, g =9,81 м/с2;
ρ – плотность материала, из которого выполнено колесо (для стали ρ =7900 кг/м3);
V З K – объём зубчатого колеса, м3;
Объём V З K зубчатого колеса определяем, исходя из его геометрических размеров, указанных в табл. 1.9 и рассчитанных в разделе 4.3. Результат расчёта объёма: V З K=0,044 м3.
Вес зубчатого колеса определяем по формуле (4.7):
G З K =7900·0,044·9,81=3410 н;
Вес муфты сцепления можно приближённо принять следующим:
G мс = (1,1…1,3)G зк, откуда
G МС=1,3·3410=4430 н;
По формуле (4.6) находим вес муфты с зубчатым колесом:
G М =3410+4430=7840 н.
Если вместо зубчатого колеса на главном валу установлен маховик (ведомый шкив клиноремённой передачи), то вес муфты сцепления можно приближённо принять, как:
G МС = (0,4…0,6)G М, (4.8)
где G М – вес маховика.
Расчёт деформирующей силы Р D на ползуне, допускаемой прочностью главного вала, можно выполнять в прикладной программе обработки электронных таблиц «MS Excel». В связи с тем, что в процессе расчёта силы Р D может возникнуть необходимость уточнения величины 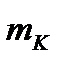 из-за возможной корректировки диаметров вала, то целесообразно расчёт силы Р D проводить в том же рабочем листе Excel, в котором выполнялся расчёт
из-за возможной корректировки диаметров вала, то целесообразно расчёт силы Р D проводить в том же рабочем листе Excel, в котором выполнялся расчёт 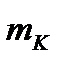 . Расчёт ведём в следующей последовательности (рис. 4.6):
. Расчёт ведём в следующей последовательности (рис. 4.6):
1. Копируем рабочий лист Excel, в котором выполнен расчёт 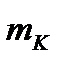 , присваиваем ему другое имя и затем открываем его.
, присваиваем ему другое имя и затем открываем его.
2. Столбцам J, K, L, M, N, O и P присваиваем имена, например, «l1», «σ(-1)», «Z1», «Z2», «Z3», «PD» и «PH» соответственно. Имена заносим в ячейки J1 – P1.
3.В ячейку J2 в соответствие с формулой l1= lСТ /2 (см. табл. 2.3) записываем формулу для расчёта длины l1. Длину l1 рассчитываем в метрах (м). После определения значения l1 в этой ячейке вносим это значение l1 в остальные ячейки J3–J11. Формат ячеек – числовой, число десятичных знаков – 3.
4. В ячейки K2–K11 записываем значение предела выносливости по нормальным напряжениям для выбранного в проектном расчёте материала вала. Значение напряжения записываем в Па (н/м2). Формат ячеек – числовой, число десятичных знаков – 0.
5. В ячейку L2 в соответствие с формулой (4.3) записываем формулу для расчёта значения комплекса Z1. После определения значения комплекса Z1 в этой ячейке определяем значения Z1 в остальных ячейках L3–L11. Формат ячеек – числовой, число десятичных знаков – 0.
6. В ячейку М2 в соответствие с формулой (4.4) записываем формулу для расчёта значения комплекса Z2. После определения значения комплекса Z2 в этой ячейке определяем значения Z2 в остальных ячейках M3–M11. Формат ячеек – числовой, число десятичных знаков – 0.
7. В ячейку N2 в соответствие с формулой (4.5) записываем формулу для расчёта значения комплекса Z3. После определения значения комплекса Z3 в этой ячейке определяем значения Z3 в остальных ячейках N3–N11. Формат ячеек – числовой, число десятичных знаков – 5.
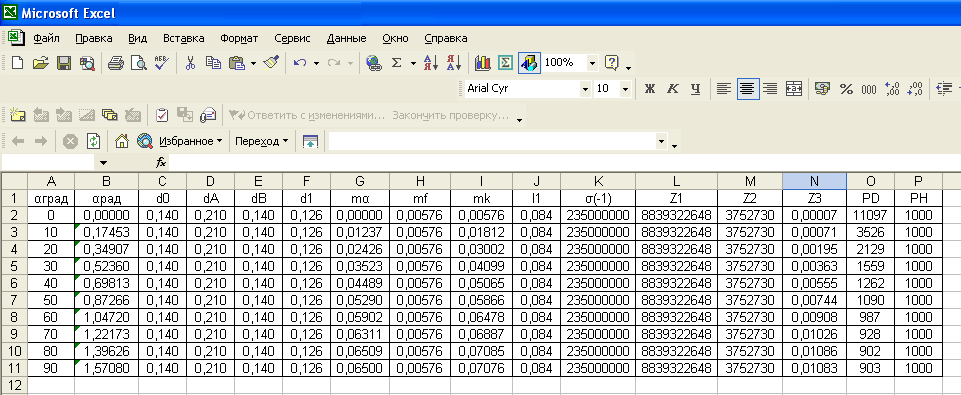
Рис. 4.6 Расчёт силы Р D на ползуне, допускаемой прочностью главного вала (расчёт выполнен в программе MS Excel)
8. В ячейку O2 в соответствие с формулой (4.1) записываем формулу для расчёта значения деформирующей силы Р D. В формуле предусматриваем ещё одно действие – деление на 1000, для получения силы Р D в кН. После определения значения силы Р D в этой ячейке определяем значения силы Р D в остальных ячейках O3–O11. Формат ячеек – числовой, число десятичных знаков – 0.
9. В ячейки P2–P11 записываем значение номинальной силы Р H. Значение силы записываем в кH. Формат ячеек – числовой, число десятичных знаков – 0.
По найденным значениям Р D и значению номинальной силы Р H строим на одной координатной плоскости два графика: график зависимости Р D =Р D (α) и график Р H =1000 кН =const. Полученные графики показаны на рис. 4.7. Абсцисса α точки пересечения графиков составляет 60º и лежит в диапазоне номинальных углов (55…65º) для данного типа пресса (см. табл. 2.7) т.е. α=αН =60º. График, обозначенный точками АВС, представляет собой график сил на ползуне, допускаемых прочностью деталей кривошипной машины (график допустимых сил на ползуне). На этом расчёт считается законченным. В случае, если окажется, что α≠αН, тогда необходимо выполнить корректировку диаметров вала (или в крайнем случае изменить материал вала) и снова рассчитать Р D, и так до тех пор, пока не будет выполнено условие α≈αН.
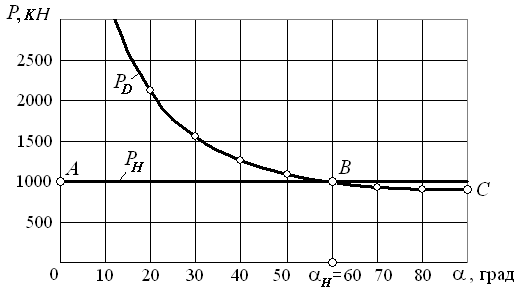
Рис. 4.7 Графики Р D =Р D(α), Р H =1000 кН и график (АВС) сил на ползуне, допускаемых прочностью главного вала (график допустимых сил на ползуне)
Дата: 2019-02-02, просмотров: 707.