Изменение нагрузки на главном валу происходит с периодическим возрастанием деформирующей силы Р D (при расчёте вала деформирующую силу будем обозначать с нижнем индексом «D») и вращающего момента М В от нуля до максимального значения с последующим спадом вновь до нуля. То есть вал работает в условиях длительного воздействия знакопеременных напряжений, которые могут привести к усталостному разрушению вала. Поэтому проверочный расчёт валов проводят на циклическую (усталостную) прочность при переменном цикле напряжений.
На практике установлено, что основным видом разрушения главных валов является усталостное разрушение, которое происходит вследствие возникновения в сечениях вала знакопеременных напряжений, обусловленных периодическим характером изменения нагрузки.
Статическое разрушение наблюдается значительно реже. Происходит оно под действием случайных кратковременных перегрузок.
Поэтому для валов основным видом расчёта является расчёт на циклическую (усталостную) прочность.
При расчёте валов на циклическую прочность необходимо установить характер цикла действующих напряжений. Для валов кривошипных машин цикл напряжений принимают симметричным для напряжений изгиба (рис. 2.11 а) и отнулевым для напряжений кручения (рис. 2.11 б).
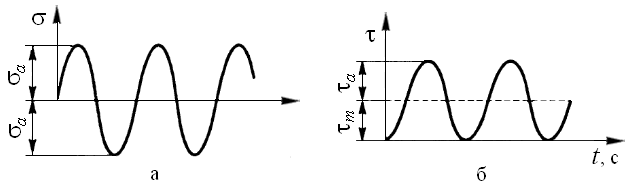
Рис. 2.11 Циклы изменения напряжений изгиба (а) и напряжений кручения (б) в сечениях вала
Расчёт вала на циклическую прочность заключается в определении запаса циклической прочности n и сравнении его с допускаемым запасом циклической прочности [n]:
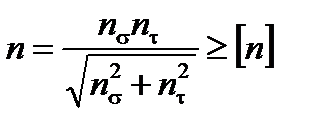 , (2.9)
, (2.9)
где nσ – запас циклической прочности по нормальным напряжениям;
nτ – запас циклической прочности по касательным напряжениям;
Запасы циклической прочности по нормальным напряжениям nσ и по касательным напряжениям nτ определяют по следующим формулам:
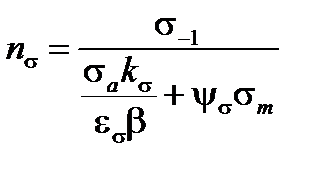 (2.10)
(2.10)
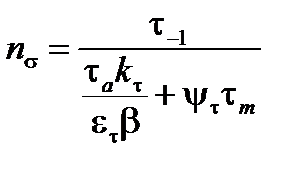 , (2.11)
, (2.11)
где kσ и kτ –эффективные коэффициенты концентрации напряжений при изгибе и кручении соответственно;
εσ и ετ – масштабные факторы при изгибе и кручении соответственно;
β – коэффициент, учитывающий состояние поверхности (фактор шероховатости);
σm и τm – постоянные составляющие циклов напряжений (средние напряжения цикла);
σа и τа – переменные составляющие циклов напряжений;
Согласно принятому выше условию (см. рис. 2.11) при расчёте валов:
σm=0; σа= σmax;
τm= τа=0,5τmax;
ψσ и ψτ – коэффициенты, корректирующие влияние постоянной составляющей цикла напряжений на циклическую прочность (см. табл. 2.4);
σ–1 и τ–1 – предел выносливости по нормальным напряжениям и по касательным напряжениям соответственно (см. табл. 2.4);
σmax= М И /0,1d3 (2.12)
τmax= М K /0,2d3 + 1,7Q /d2 , (2.13)
где М И – изгибающий момент в расчётном сечении вала диаметром d;
М K – крутящий момент в этом же сечении;
Q – поперечная сила в расчётном сечении вала.
Допускаемые значения [n] приведены в табл. 2.5 ([19, с.119]).
Таблица 2.5
Допускаемые значения [n] для валов различных типов кривошипных машин
| № п/п | Тип кривошипной машины | Допускаемый запас циклической прочности [n] |
| 1 | Листоштамповочные одно-, двух- и четырёхкривошипный прессы | 1,3 |
| 2 | ГКМ | 1,2…1,3 |
| 3 | КГШП | 1,5 |
| 4 | Чеканочные прессы | 1,5 |
| 5 | Автоматы листоштамповочные | 1,6…1,8 |
| 6 | Автоматы для объёмной штамповки | 1,7…2,0 |
После подстановки всех величин в формулу (2.9) получим:
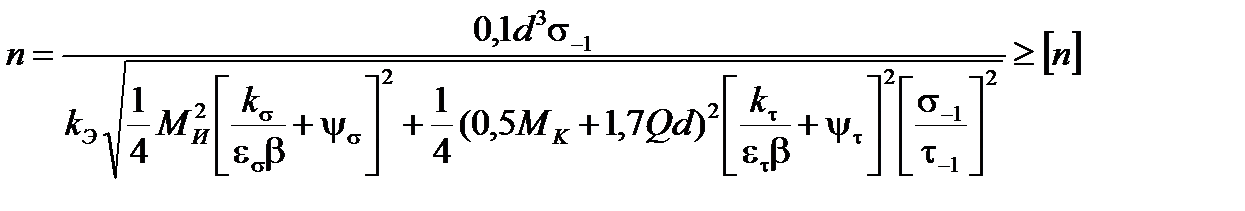
(2.14)
Коэффициент k Э, стоящий в знаменателе полученного выражения, называют коэффициентом эквивалентной нагрузки. Он учитывает характер режима нагружения. С помощью этого коэффициента осуществляется замена действующей (реальной) переменной нагрузки постоянной (расчётной) нагрузкой, эквивалентной действующей. Ориентировочные значения k Э в зависимости от типа кривошипной машины приведены в табл. 2.6 ([1, с.58], [19, с.113], [16, с.133]).
Таблица 2.6
Коэффициент эквивалентной нагрузки k Э
| № п/п | Тип кривошипной машины | Значения коэффициента k Э |
| 1 | Прессы универсальные | 0,8 |
| 2 | Прессы-автоматы | 1,0 |
При проектировании кузнечно-штамповочного оборудования расчёт главных валов традиционно ведут не путём определения n и проверки выполнения условия n ≥ [n], а путём определения деформирующей силы на ползуне Р D, допускаемой прочностью главного вала. Для этого внешние силовые факторы М И, М K и Q, входящие в уравнение (2.9), выражают через Р D и затем решают это уравнение относительно Р D. Моменты М И, М K и поперечная сила Q могут быть выражены через Р D следующим образом:
М И = Р D Uи, М K = Р D Uк, Q= Р D Uc (2.15)
где U И – коэффициент, представляющий собой приведённое плечо силы, вызывающей появление изгибающего момента;
U K – коэффициент, равный величине mк, т.е. Uк = mк, либо величине 0,5 m K , т.е. U K = 0,5 m K, в зависимости от вида расчётной схемы вала. Здесь m K – приведённое плечо деформирующей силы (эту величину называют ещё относительным вращающим моментом).
U С – коэффициент поперечной силы.
В уравнение (2.9) введём два коэффициента Фσ и Фτ :
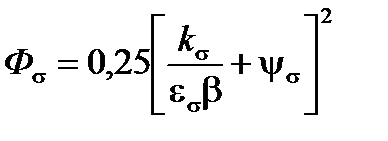 (2.16)
(2.16)
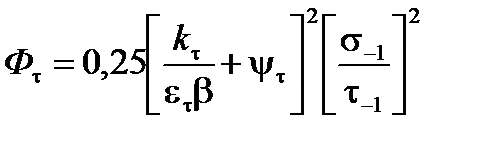 (2.17)
(2.17)
и подставим в него выражения (2.15). В результате получим:
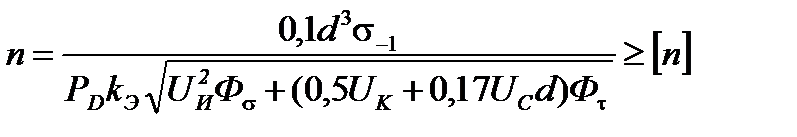 (2.18)
(2.18)
Решив это уравнение относительно Р D , окончательно получим:
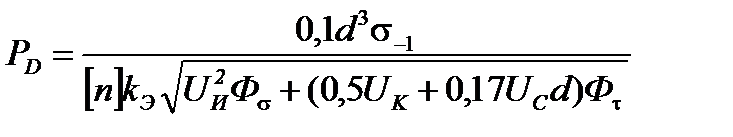 (2.19)
(2.19)
Полученная формула является общей, т.е. с её помощью может быть выполнен расчёт главного вала любой кривошипной машины. Но особенность её заключается в том, что коэффициенты U И, U K и U С, входящие в её структуру, определяются для каждого типа вала по-разному. Методика определения коэффициентов U И, U K и U С зависит от расположения опасного сечения вала, от конструктивного исполнения вала, а также от особенностей расположения на нём различных элементов (маховика, зубчатого колеса, муфты, тормоза). Опыт проектирования кривошипных машин показал, что всё многообразие конструктивных исполнений главных валов можно свести к 14-и расчётным схемам. Поэтому для каждой из них были определены коэффициенты U И, U K и U С и выведены формулы для расчёта силы Р Д на ползуне, допускаемой прочностью главного вала. Эти расчётные схемы и формулы приведены в книге [16, с.355] и в учебном пособии [9, с.151]. Задача проектировщика заключается в правильном выборе расчётной схемы вала, формул к ней и последующем расчёте по этим формулам значений силы Р D.
Например, расчётной схемой для коленчатого одноколенного вала с односторонним клиноремённым приводом (с маховиком) является расчётная схема №3 (рис. 2.12).
На этой схеме обозначены три опасных сечений вала: А, В и Е. Для каждого из них рассчитывают силу Р D по соответствующей формуле. Например, для сечения В-В:
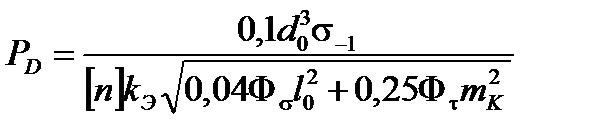 при
при 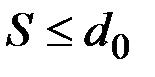 (2.20)
(2.20)
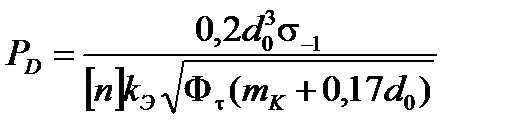 при
при 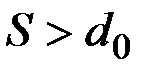 , (2.21)
, (2.21)
где S – ход ползуна (Smax = H);
d0 – диаметр опорной шейки вала;
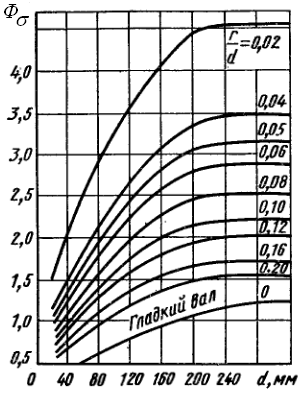
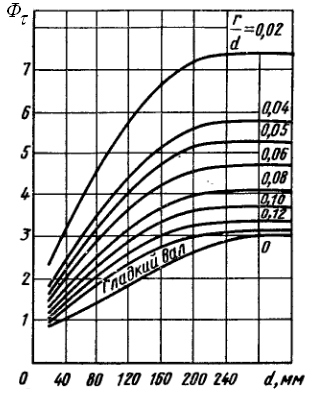
Значения коэффициентов Фσ и Фτ , входящих в формулы для определения силы Р D, можно рассчитать либо по формулам (2.16 и 2.17), воспользовавшись для этого справочной литературой [17,24], либо определить по графикам, изображённым на рис. 2.13 а, б, в, г ([1,с.55], [9,с.147], [16,с.137]). По этим графикам значения Фσ и Фτ для диаметров d > 280 мм будут такими же, как и для диаметра d = 280 мм.
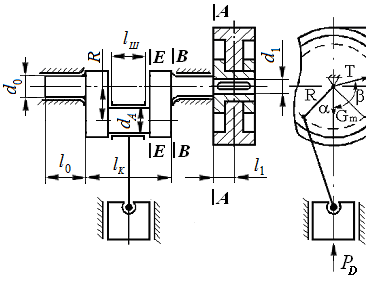
Рис. 2.12 Расчётная схема №3. Коленчатый одноколенный вал с односторонним клиноремённым приводом (с маховиком)
Анализ уравнений (2.19-2.21) для определения допускаемой силы P D показывает, что эта сила зависит от величины m K, являющейся функцией угла поворота кривошипа (см. раздел 2.3, рис. 2.10). Другие параметры, входящие в эти уравнения, для данных условий работы остаются постоянными. Поэтому допускаемая сила P D также будет изменяться при повороте кривошипа, в связи с чем расчёт силы Р D проводят при различных значениях m K в диапазоне изменения угла α от 0 до π/2. Шаг изменения угла α обычно принимают равным 10º (см. раздел 2.3). Указанный диапазон изменения угла α объясняется тем, что, как уже было сказано выше, практически все технологические операции выполняются в этом диапазоне углов.
а б
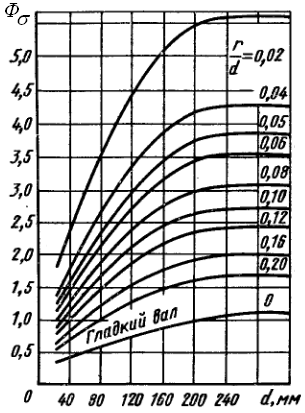
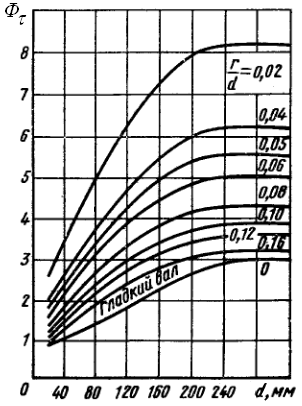
в г
Рис. 2.13 Значения Фσ и Фτ для нормализованной стали 45 (а, б) и для улучшенных сталей 40Х и 40ХН (в, г)
Затем по найденным значениям Р D строят график силы на ползуне, допускаемой прочностью главного вала, общий вид которого показан на рис. 2.14.
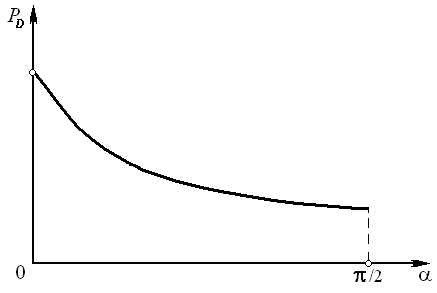
Рис. 2.14 График силы на ползуне, допускаемой прочностью главного вала
Дата: 2019-02-02, просмотров: 798.