Машины
Для работы пресса в обычных условиях характерен весьма неравномерный расход энергии в течение одного технологического цикла. У большинства кривошипных машин рабочий ход, связанный с совершением полезной работы и характеризующийся повышенными затратами энергии, занимает очень малую часть технологического цикла (около 10%). В течение остальной части цикла (≈90%) затраты энергии невелики. Эта часть цикла соответствует холостым ходам машины: приближение ползуна к заготовке и возвращение его в исходное положение после окончания операции.
Если использовать для привода такой машины только электродвигатель, то его установочная мощность оказалась бы очень большой, но использовалась бы лишь в очень короткие периоды рабочей нагрузки. Для снижения установочной мощности двигателя и повышения плавности работы привода прибегают к аккумулированию энергии путём установки в приводе быстровращающихся маховиков – массивных деталей в форме диска с утолщённым ободом.
Во время холостого хода двигатель разгоняет маховик, и он накапливает значительную энергию. При рабочем ходе энергию, необходимую для совершения полезной работы, отдаёт не только электродвигатель, но и маховик, причём основная часть энергии приходится на долю маховика. Здесь необходимо подчеркнуть, что во время рабочего хода энергию отдаёт не только маховик, но и другие вращающиеся детали (маховые массы) привода, т.е. фактически роль маховика выполняет весь привод, а не только сам маховик. Особенно это заметно в мощных машинах, например в КГШП. Ориентировочно можно считать, что для КГШП момент инерции собственно маховика J М составляет всего лишь 70…75% от момента инерции вращающихся масс привода J ПР, т.е.:
J М =(0,70…0,75) J ПР, (3.1)
для горизонтально-ковочных машин (ГКМ):
J М =(0,85…0,90) J ПР, (3.2)
для большинства кривошипных машин с муфтой в маховике, для лёгких универсальных прессов и для пресс-автоматов:
J М =(0,97…0,99) J ПР . (3.3)
В приводе кривошипных машин маховик обычно используется в качестве одного из элементов передач, например, как ведомый шкив клиноремённой передачи или в качестве одного из колёс зубчатых передач. В более сложных механизмах маховик может быть выполнен заодно с муфтой включения.
Определение потребной мощности электродвигателя.
Выбор типа электродвигателя
Большинство современных кривошипных машин оборудуются приводом с асинхронным трёхфазным двигателем с короткозамкнутым ротором и синхронной частотой вращения 1500 об/мин. Применение данных типов электродвигателей объясняется простотой их устройства, невысокой стоимостью, надёжностью и безопасностью работы.
Характеристика асинхронного электродвигателя. На рис 3.1 показана характеристика асинхронного двигателя, выражающая зависимость частоты вращения n вала электродвигателя от нагрузки, т.е. величины вращающего момента M.
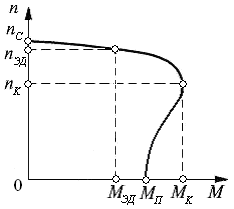
Рис. 3.1 Характеристика асинхронного электродвигателя:
МЭД – номинальный вращающий момент; МП – момент, развиваемый при пуске двигателя; М K – кратковременный (максимальный) вращающий момент; n ЭД – номинальная частота вращения; n K –критическая частота вращения; n C – синхронная частота вращения (при отсутствии нагрузки), т.е. частота вращения магнитного поля статора, зависящая от частоты электрического тока f и числа пар полюсов статора р (n С =60f /р)
При стандартной частоте тока f = 50с–1 и числе пар полюсов р от 1 до 6 синхронная частота вращения двигателя соответственно составляет n с = 3000; 1500; 1000; 750; 600 и 500 об/мин. Чем выше частота вращения вала двигателя (при одном и том же значении мощности), тем меньше габариты двигателя и его масса.
Частота вращения n ЭД, указываемая в каталогах [6, с.898] электродвигателей, относится к номинальному режиму и является номинальной (асинхронной) частотой вращения. Именно эту частоту необходимо задавать при определении общего передаточного числа привода.
Под действием нагрузки частота вращения вала электродвигателя уменьшается по сравнению с синхронной частотой вращения n С и возникает скольжение s:
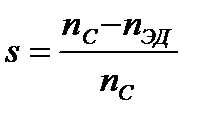, (3.4)
Иногда в каталогах на электродвигатели задают не номинальную частоту вращения n ЭД, а величину скольжения s Н, соответствующую номинальному режиму. В этом случае n ЭД определяется по формуле:
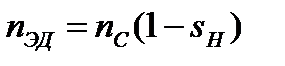(3.5)
Электродвигатель выбирают по потребной мощности N таким образом, чтобы его номинальная мощность, указанная в каталоге, была больше потребной, т.е. N ЭД ≥ N . Рекомендуется выбирать тип электродвигателя с синхронной частотой вращения n С =1500 об/мин. Номинальную частоту вращения n ЭД для выбранного двигателя выбирают из таблицы или рассчитывают по формуле (3.5).
Расчёт потребной мощности электродвигателя. Потребная мощность электродвигателя N (кВт) определяется по следующей формуле [16, с.111]:
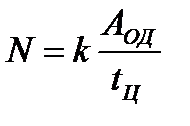, (3.6)
где k – коэффициент запаса;
А ОД – работа, совершаемая прессом за цикл одиночного хода (кДж);
t Ц – время цикла (с).
Коэффициент запаса k зависит от величины номинального скольжения s Н, которое, в свою очередь, зависит от фактического числа одиночных ходов ползуна в минуту n ОД (см. табл. 3.1).
Таблица 3.1
| nОД | sН | k | ε |
| До 15 15…30 Свыше 30 | 0,12…0,08 0,08…0,04 0,04…0,02 | 1,2 1,3 1,4…1,6 | 0,85 0,90 0,95 |
Число одиночных ходов ползуна в минуту равно:
n ОД = р n, (3.7)
где р – коэффициент использования числа ходов (см. табл. 3.2), n – число двойных холостых ходов ползуна в минуту (номинальное число ходов ползуна).
Таблица 3.2
| Тип кривошипного пресса | р |
| Однокривошипный простого действия Однокривошипный простого действия двухстоечный Кривошипные горячештамповочные (КГШП) Горизонтально-ковочные машины (ГКМ) Чеканочные Холодно-высадочные автоматы Прессы обрезные Ножницы | 0,30...0,75 0,30...0,40 0,12...0,25 0,20...0,35 0,60...0,80 1,00 0,30 0,70...0,90 |
Время цикла t Ц:
t = 60/nОД (3.8)
Работа А ОД, совершаемая прессом за цикл одиночного хода:
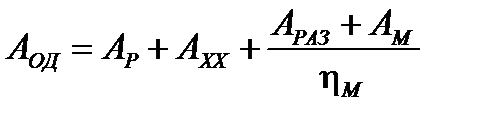, (3.9)
где АР – работа, совершаемая за время рабочего хода;
А ХХ – работа, затрачиваемая на совершение холостого хода;
А РАЗ – работа, затрачиваемая на разгон ведомой части муфты;
А М – работа, затрачиваемая на преодоление сил трения на фрикционных поверхностях муфты при её включении;
η М – к.п.д. передачи от вала муфты к электродвигателю
Работа АР состоит, в свою очередь, из следующих составляющих:
АР = А ПЛ + А f + А УП + А УПР f , (3.10)
где А ПЛ – работа пластической деформации (полезная работа деформирования);
А f – работа, затрачиваемая на преодоление сил трения;
А УПР – работа, затрачиваемая на упругую деформацию элементов кривошипной машины;
А УПР f – работа, затрачиваемая на преодоление сил трения, возникающих при упругой деформации кривошипной машины;
Ориентировочные данные о структуре энергетических затрат одиночного хода приведены в табл. 3.3.([16, с.115]).
Таблица 3.3
Структура энергетических затрат одиночного хода различных типов прессов
| Тип кривошипной машины | А ПЛ | А f | А УПР f |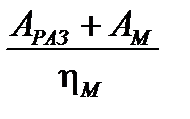 
| А ХХ | Всего |
| Универсальные одно- стоечные и двухстоечные | 1 | 0,6-1,2 | 0,0-0,3 | 0,3-0,8 | 0,5-1,2 | 2,4-2,5 |
| Однокривошипные закрытые | 1 | 0,5-1,0 | 0,0-0,4 | 0,3-0,4 | 0,3-0,4 | 2,1-3,2 |
| Двухкривошипные | 1 | 0,3-1,0 | 0,2-0,5 | 0,7 | 0,3-0,4 | 2,5-3,6 |
| Обрезные | 1 | 0,9 | 0,2 | 0,3 | 0,3 | 2,7 |
| Горячештамповочные (КГШП) | 1 | 1,0 | 0,8-1,0 | 0,2-0,5 | 0,3-0,5 | 3,3-4,0 |
| Чеканочные | 1 | 1,0 | 0,3-0,7 | 0,3-0,4 | 0,6 | 3,2-3,7 |
| Автоматы холодно- высадочные | 1 | 0,5-1,0 | 0,5-0,8 | – | 1,5-2,5 | 3,5-5,3 |
Табл. 3.3 составлена на основе обобщённых расчётных и экспериментальных данных. Для облегчения сравнения полезная работа пластической деформации А ПЛ принята за 1, остальные составляющие работы приводятся по отношению к ней. Эти данные не совсем точны, поэтому самым лучшим средством определения энергетических параметров системы является расчёт. Однако аналитический расчёт некоторых составляющих работ, в частности А ХХ, А М и А РАЗ весьма сложен, поэтому для их приближённого определения пользуются данными табл. 3.3. Работы АР и А ПЛ определяют графоаналитическими и аналитическими способами.
Работы А ХХ и (А РАЗ + А М )/ η М составляют некоторую часть от работы пластического деформирования А ПЛ (см. табл. 3.3), причём величина этих частей зависит от типа и назначения пресса. Обозначив эти части через a и b, получим:
А ХХ = a А ПЛ (3.11)
(А РАЗ + А М)/ η М = b А ПЛ (3.12)
Работа А ПЛ пластической деформации определяется по приближённой зависимости:
А ПЛ = δ P H H , (3.13)
где δ – коэффициент полноты технологической операции, зависит от типа кривошипной машины (см. табл. 3.4) [16, с.107-108, с.117];
P H – номинальная сила;
H – максимальный ход ползуна.
Таблица 3.4
Значения коэффициентов δ
| Тип кривошипной машины | δ |
| Однокривошипные прессы открытые простого действия: исполнение 1……………………………………………………… исполнение 2……………………………………………………… | 0,03 0,04 |
| Однокривошипные прессы закрытые простого действия: исполнение 1……………………………………………………… исполнение 2……………………………………………………… исполнение 3……………………………………………………… | 0,04 0,09 0,03 |
| Двухкривошипные и четырёхкривошипные прессы: исполнение 1……………………………………………………… исполнение 2……………………………………………………… | 0,04 0,09 |
| Однокривошипные прессы двойного действия | 0,15 |
| Чеканочный пресс | 0,01-0,04 |
| Горячештамповочный пресс (КГШП) | 0,02-0,03 |
| Горизонтально-ковочная машина (ГКМ) | 0,03-0,06 |
| Холодно-высадочный автомат | 0,01-0,04 |
Работа АР может быть определена графоаналитическим способом. В этом способе АР определяется как площадь под графиком зависимости M В = M В(α), где M В – вращающий момент на главном валу, α – угол поворота кривошипа в пределах рабочего хода. Величину M В можно определить из следующего выражения:
M В = Pm K , (3.14)
где P – деформирующая сила, соответствующая углу поворота кривошипа α при выполнении конкретной технологической операции (в период рабочего хода);
m K – приведённое плечо деформирующей силы при том же угле поворота кривошипа.
Таким образом для расчёта значений M В по формуле (3.14) необходимо знать зависимости m K = m K(α) и P=P(α) и подставлять в формулу значения P и m K, которые соответствуют одним и тем же значениям α.
Определение значений приведённого плеча деформирующей силы m K и построение графика зависимости m K = m K(α) показаны в разделе 2.3.
Рассмотрим теперь порядок построения графика P=P(α). Основой для построения графика P=P(α) служат так называемые типовые графики рабочих нагрузок, которые представляют собой графики кусочно-линейных функций, изображённых на рис. 3.2 и 3.3 ([1, с.128]).
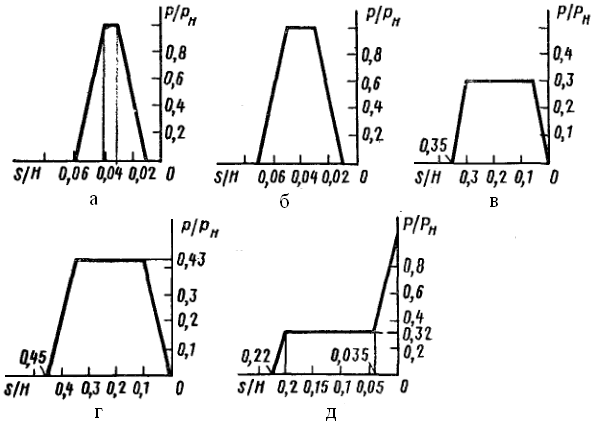
Рис. 3.2 Типовые графики рабочих нагрузок для универсальных штамповочных прессов: а – вырубка; б – вырубка при увеличенном ходе; в – вытяжка; г – вытяжка на прессе двойного действия; д – гибка
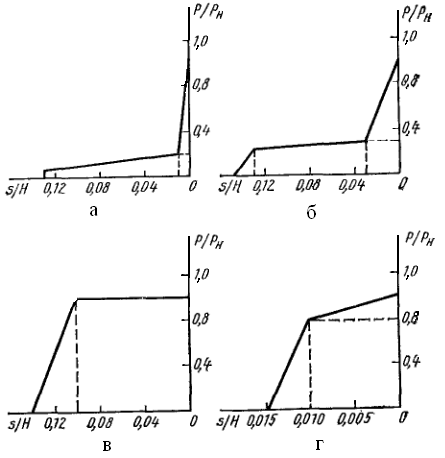
Рис. 3.3 Типовые графики рабочих нагрузок прессов для объёмной штамповки:
а – горячая штамповка; б – горячее выдавливание; в – холодное выдавливание; г – холодная калибровка-чеканка
Типовые графики строят на основе реальных графиков рабочих нагрузок P=P(S), характер изменения которых для большинства операций штамповки известен и показан на рис. 3.4 [19, с.127]. Однако для выполнения энергетических расчётов кривошипных машин нет необходимости иметь точную форму графика, а достаточно знать только координаты характерных точек графика (координаты экстремальных точек, точек перегиба и точек пересечения графика с осями координат). Вот почему типовые графики выполнены в виде отрезков прямых.
Типовые графики рабочих нагрузок строят в относительных координатах: по оси абсцисс откладывают текущие значения перемещений S ползуна при деформировании, отнесённые к максимальной величине хода ползуна H, т.е. S/H, а по оси ординат – текущие значения силы деформирования P, отнесённые к номинальной силе P Н разрабатываемой кривошипной машины, т.е. P/P Н. Поскольку графики эти строят без учёта упругих деформаций элементов машины, то они являются универсальными для любых типов кривошипных машин. Например, типовым графиком рабочих нагрузок для операции вытяжки, реальный график которой изображён на рис. 3.4 а, является график, показанный на рис. 3.2 в.
Графики эти имеют одну особенность, которая заключается в том, что при совершении технологической операции отсчёт перемещений ползуна по оси абсцисс «0–S/H» идёт справа налево, а изменение величины деформирующей силы – слева направо, т.е. наоборот. Связано это с принятым направлением отсчёта перемещений ползуна, которое противоположно направлению его фактического перемещения (см. раздел 1.6).
Для того, чтобы на основе типового графика рабочих нагрузок построить график рабочих нагрузок для конкретной технологической операции, выполняемой на кривошипной машине с заданной технической характеристикой, необходимо выполнить следующие действия: 1) выбрать соответствующий типовой график для этой операции; 2) найти абсолютные значения координат характерных точек графика; 3) соединить эти точки прямыми линиями.
Выше было сказано, что типовые графики рабочих нагрузок строят без учёта упругой деформации элементов деталей машины. В реальных же условиях эксплуатации под действием нагрузки возникает упругая деформация элементов кривошипной машины: прогибается главный вал и стол пресса, деформируется станина и т.д. Величина этой деформации может достигнуть нескольких миллиметров.
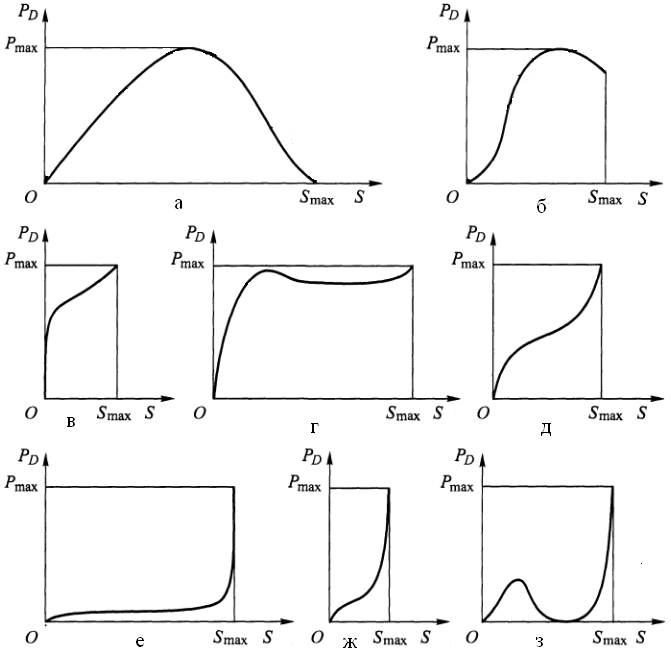
Рис. 3.4 Графики рабочих нагрузок (деформирующей силы):
а – вытяжка листового металла; б– вырубка-пробивка; в – чеканка и калибровка; г – прессование и выдавливание; д – прямое прессование; е, ж – объёмная штамповка в открытых и закрытых штампах; з – гибка в штампах
В результате этого поверхности верхней и нижней половин штампа могут не сомкнуться, что приведёт к недоштамповке заготовки, т.е. к получению некачественной поковки. Чтобы этого не произошло, необходимо увеличить ход ползуна на величину этой упругой деформации, т.е. совершить дополнительную работу. Для того чтобы в процессе энергетического расчёта машины учесть эту дополнительную работу необходимо построить суммарный график рабочих нагрузок, т.е. график рабочих нагрузок с учётом упругой деформации деталей машины. На этом графике ход ползуна S У с учётом упругой деформации определяется как сумма рабочего хода ползуна S, рассчитанного по типовому
графику, и удлинения Δl элементов машины за счёт упругой деформации:
S У = S + Δl (3.15)
Величина упругой деформации Δl определяется исходя из характеристики жёсткости кривошипной машины (рис. 3.5), которая представляет собой зависимость между величиной упругой деформации машины Δl и величиной нагрузки Р в диапазоне нагрузок от 0 до Р Н.
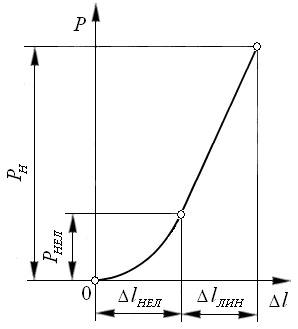
Рис. 3.5 Характеристика жёсткости кривошипной машины
Нелинейный участок кривой учитывает выборку зазоров и нелинейную упругую деформацию стыков в начальной фазе нагружения. Сила Р, соответствующая этой деформации, обычно не превышает 25…30% от номинальной силы Р Н, поэтому на практике используют только линейную часть графика, которая характеризуется коэффициентом жёсткости С:
С =Р/Δl (3.16)
Из формулы (3.16) определяется величина упругой деформации при заданной величине нагрузки:
Δl =Р/С (3.17)
Коэффициент жёсткости С определяется эмпирическим путём на основе практических данных. Приближённые значения С для различных видов кривошипных машин приведены в табл. 3.5 ([16, с.344,350]).
Таким образом, для построения суммарного графика рабочих нагрузок (с учётом упругой деформации машины) необходимо сначала в соответствие с данными табл. 3.5 определить коэффициент жёсткости машины С, затем для каждой характерной точки графика рабочих нагрузок (полученного на основе типового графика) по формуле (3.17) определить величину дополнительного хода ползуна Δl, который он совершает за счёт упругой деформации машины, затем по формуле (3.15) рассчитать общий ход ползуна для каждой характерной точки и, наконец, на основе полученных данных построить суммарный график рабочих нагрузок Р=Р(S).
Таблица 3.5
Коэффициенты жёсткости кривошипных машин С
| Тип кривошипной машины | С, кН/мм (PH , кН) | С, МН/м (PH , МН) |
| Прессы одностоечные открытые и двухстоечные наклоняемые |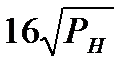 
| 
|
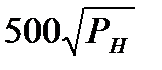
| Прессы чеканочные |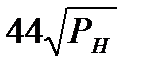 
| 
|
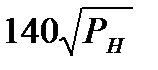
| Прессы горячештамповочные (КГШП) |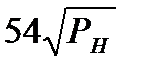 
| 
|
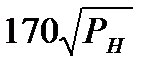
| Холодновысадочные автоматы |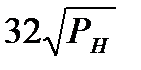 
| 
|
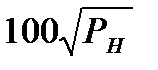
Следующим шагом к получению графика Mв = Mв(α) служит процесс преобразования полученного суммарного графика рабочих нагрузок Р=Р(S) в график P =P(α). Для этого на суммарном графике рабочих нагрузок нужно поменять ось 0S на ось 0α так, чтобы для характерных точек графика значениям αi на новой оси 0α соответствовали бы значениям Si на заменённой оси 0S. После определения всех значений αi, соответствующих значениям Si, строят график P=P(α).
И заключительным шагом в определении работы A Р служит построение графика зависимости M В = M В(α). Как было сказано выше. значения M В получают путём умножения значений P, взятых из построенного графика P=P(α), на значения m K, взятые из графика зависимости m K = m K(α) (см. раздел 2.3). Причём значения P и m K берутся при одних и тех же значениях угла α. Для нахождения значений m K необходимо воспользоваться рабочим листом Excel с расчётами m K (см. раздел 2.3). Подставив в ячейку столбца А значение угла αi , получают искомое значение m K.
Дата: 2019-02-02, просмотров: 701.
