Для классификации входных векторов необходимо создать нейронную сеть в виде персептрона, который разделяет векторы входа на два класса. Обозначим эти классы как 0 и 1. Обучающую последовательность сформируем в виде двух массивов ячеек: массива входов Р = {[2; 2] [1; 2] [–2; 2] [–1; 1] [1; –2]} и массива целей Т = {0 0 1 1 1}, который задает принадлежность каждого вектора входа к определенному классу. Выполним эту операцию в рабочей области системы MATLAB, а затем импортируем их в рабочую область интерфейса NNTool.
Зададим персептрон с одним нейроном, функцией активации HARDLIM и правилом настройки LEARNP. Для этого из списка нейронных сетей выберем тип сети Perceptron (рисунок 5.11) и зададим требуемые параметры.

Рисунок 5.11 – Выбор типа сети типа Perceptron
Чтобы увидеть структурную схему сети, воспользуемся кнопкой View (рисунок 5.12).

Рисунок 5.12 – Структурная схема сети типа Perceptron
Теперь выполним инициализацию сети, используя закладку Initialize, а затем адаптацию и настройку параметров сети, используя закладку Adapt окна Network. Для этого следует указать имена входа и цели, а также задать количество циклов адаптации (в данном случае достаточно трех циклов) и нажать кнопку Adapt Network.
В результате настройки будут установлены следующие значения весов и смещений, которые можно увидеть, выбрав закладку Weights. Для данной сети вектор весов равен IW{1, 1} = [–3 –2], а смещение b{1} = 1. Таким образом, линия переключения, разделяющая плоскость на две области, описывается следующим образом:
L: –3p1 – 2p2 + 1 = 0
Перейдя в окно Network/Data Manager, можно просмотреть значения сигналов на выходе и ошибку сети (рисунок 5.13, а и б соответственно). Сделайте вывод о величине ошибки и качестве классификации.

а

б
Рисунок 5.13 – а) Значение сигналов на выходе; б) Ошибка сети
Сети Кохонена
Рассмотрим самоорганизующуюся нейронную сеть с единственным слоем, задача которой заключается в том, чтобы правильно сгруппировать (кластеризировать) поступающие на нее векторы входа. Архитектура слоя Кохонена показана на рисунке 5.14.
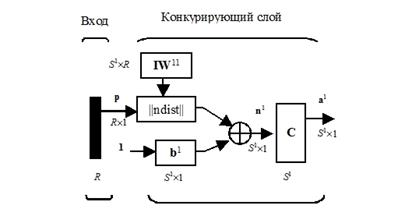
Рисунок 5.14 – Архитектура слоя Кохонена
Нетрудно убедиться, что это слой конкурирующего типа, поскольку в нем применена конкурирующая функция активации. Кроме того, архитектура этого слоя очень напоминает архитектуру скрытого слоя радиальной базисной сети. Здесь использован блок ndist для вычисления отрицательного евклидова расстояния между вектором входа p и строками матрицы весов IW11. Вход функции активации n1 – это результат суммирования вычисленного расстояния с вектором смещения b. Если все смещения нулевые, максимальное значение n1 не может превышать 0. Нулевое значение n1 возможно только в случае, когда вектор входа p оказывается равным вектору веса одного из нейронов. Если смещения отличны от 0, то возможны и положительные значения для элементов вектора n1.
Конкурирующая функция активации анализирует значения элементов вектора n1 и формирует выходы нейронов, равные 0 для всех нейронов, кроме одного нейрона – победителя, имеющего на входе максимальное значение. Таким образом, вектор выхода слоя a1 имеет единственный элемент, равный 1, который соответствует нейрону-победителю, а остальные равны 0. Такая активационная характеристика может быть описана следующим образом:
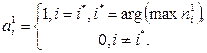
Заметим, что эта активационная характеристика устанавливается не на отдельный нейрон, а на слой. Поэтому такая активационная характеристика и получила название конкурирующей. Номер активного нейрона i* определяет ту группу (кластер), к которой наиболее близок входной вектор.
Скопируйте построчно (группами команд) и протестируйте пример, приведенный ниже.
% Этот способ обучения сети вам понадобиться, если вы не знаете цели (значение Т).
% Как видите из этого графика, система сама автоматически определила и разнесла центры кластеров.
% Также имеются параметры для тонкой настройки этой сети, их можно посмотреть при обучении сети, такие как количество эпох, градиент, погрешность и т.д.,
% к ним нужно обращаться как имя_сети.команда, например net.time
% Сеть - самоорганизующаяся сеть Кохонена
% Количество нейронов - 4
% База знаний - z
% Размерность базы знаний - 2х200
% Зададим одно из множеств значений кластера №1.
% Центром кластера будет является точка (3;0) с небольшим разбросом от центра rand(1,30) и количеством отсчетов 50.
% Т.е x1 и y1 будет являться массивом размерность 1х30
y1=0+rand(1,30)
x1=3+rand(1,30)
% посмотрим получившиеся значения (рисунок 5.15)
plot(x1,y1,'ob')
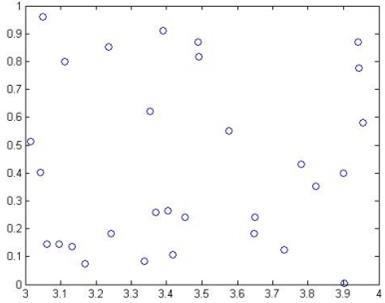
Рисунок 5.15 – Множество значений кластера 1
% Также зададим множество значений для второго кластера с центром (-3;0) (рисунок 5.16)
y2=0+rand(1,30)
x2=-3+rand(1,30)
plot(x2,y2,'or')
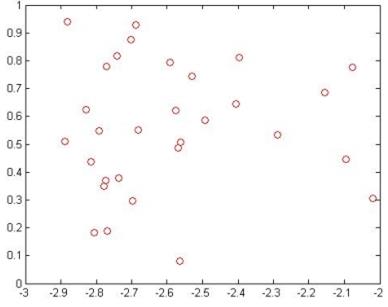
Рисунок 5.16 – Множество значений кластера 2
% Далее зададим третий и четвертый кластеры с центрами (0;3) и (0;-3)
y3=3+rand(1,30)
x3=0+rand(1,30)
x4=0+rand(1,30)
y4=-2+rand(1,30)
% Для полной наглядности посмотрим все кластеры на одном графике (рисунок 5.17)
figure (1)
hold on
plot(x3,y3,'og')
plot(x4,y4,'oy')
plot(x1,y1,'ob')
plot(x2,y2,'or')
grid on
hold off
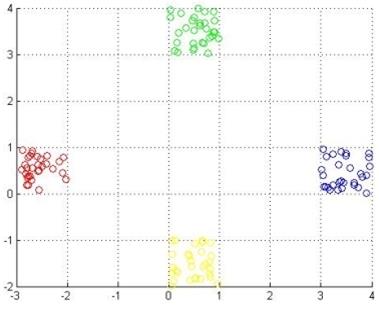
Рисунок 5.17 – Множество значений всех четырех кластеров
% Зададим цели наших четырех кластеров
T3(1:30)=10;
T4(1:30)=20;
T1(1:30)=30;
T2(1:30)=40;
% Также как в примере про feed forward сети, соединим все цели кластеров
T(1:30)=T1;
T(31:60)=T2;
T(61:90)=T3;
T(91:120)=T4;
% Перед тек подавать это на вход нейросети,
% нам необходимо соединить всю базу знаний для нейронной
% системы в одну матрицу, а именно соединим x и y и все
% это присвоим в переменную z
x(1:30)=x1;
x(31:60)=x2;
x(61:90)=x3;
x(91:120)=x4;
y(1:30)=y1;
y(31:60)=y2;
y(61:90)=y3;
y(91:120)=y4;
z(1,1:120)=x
z(2,1:120)=y
% Зададим сетку карты Кохонена гексогональную 2х2,
% так как этого нам вполне хватит
net = newsom(z,[2 2]);
% Проведем цикл обучения (рисунок 5.18)
net = train(net, z)
Заданная карта Кохонена представлена на рисунке 5.19. Распределение по кластерам всех спектров, которые мы использовали при обучении, представлено на рисунке 5.20, а распределение центров кластеров нейронной сети Кохонена – на рисунке 5.21.
% Теперь проверим получившуюся сеть на тех
% спектрах с помощью, которых мы обучали сеть
a = sim(net,z)
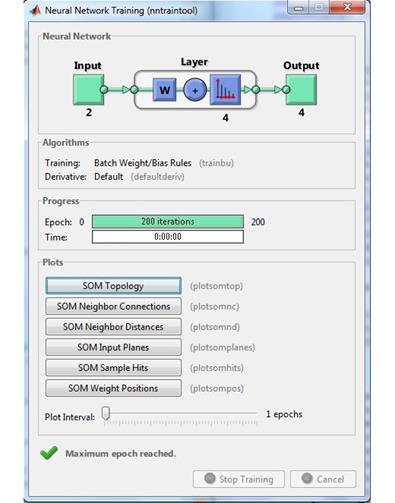
Рисунок 5.18 – Цикл обучения сети
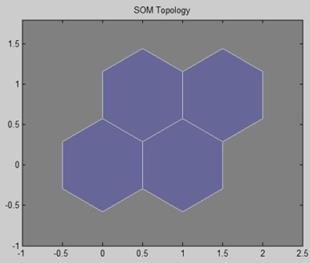
Рисунок 5.19 – Заданная карта Кохонена
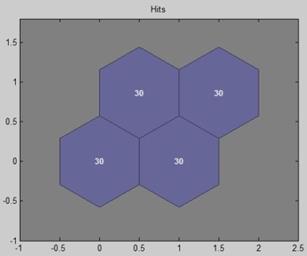
Рисунок 5.20 – Распределение по кластерам всех спектров,
используемых при обучении
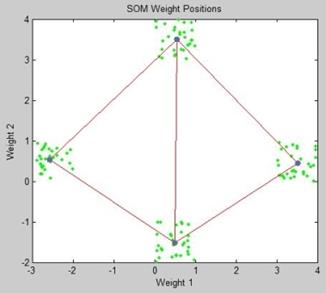
Рисунок 5.21 – Распределение центров кластеров нейронной
сети Кохонена
2.4 Задания для самостоятельной работы
1. Повторите п. 2.1 при большем объеме обучающей выборки (объем задается преподавателем). Сделайте вывод о погрешности обучения и сравните ее с изначальным результатом п. 2.1.
2. Видоизмените архитектуру сети из п. 2.2 (варианты архитектуры задаются преподавателем) и пронаблюдайте за изменением погрешности. Сделайте вывод о целесообразности выбора того или иного варианта.
3. Измените код сети Кохонена (п. 2.3) для кластеризации на шесть кластеров. Вычислите показатель ошибки обучения.
СОДЕРЖАНИЕ ОТЧЕТА
1. Цель работы.
2. Листинги написанных программ (M-файлов) в среде MATLAB для каждого задания.
3. Сводная таблица результатов, содержащая полученные в результате проведенных исследований изображения в сравнении с исходными изображениями.
4. Выводы о полученных результатах, сопоставление с теорией.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Каковы причины широкого применения нейросетей?
2. Назовите основные типы нейронных сетей, представленных в NNTool.
3. Является ли нейронная сеть линейной по своей природе?
4. Какие типы нейросетей используются в данной лабораторной работе?
5. Какие особенности имеет линейная нейронная сеть с линией задержки по входу?
6. Структурная схема нейросети в виде персептрона.
7. Что такое конкурирующая функция активации?
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Хайкин А. Нейронные сети. Полный курс // М.: Вильямс, 2006. 1104 с.
2. Дьяконов В., Круглов В. Математические пакеты расширения MatLAB. Специальный справочник // СПб: Питер, 2001. 488 с.
Учебное издание
ЦИФРОВАЯ ОБРАБОТКА
БИОМЕДИЦИНСКИХ ИЗОБРАЖЕНИЙ
Методические указания к лабораторным работам
Составитель: Мякинин Олег Олегович
Самарский национальный исследовательский университет
имени академика С.П. Королева
443086, Самара, Московское шоссе, 34
Дата: 2019-02-02, просмотров: 950.