В обработке изображений первые производные реализуются через модуль градиента. Для функции f(x, y) градиент f в точке (x, y) определяется как двумерный вектор-столбец:

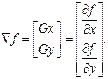
Модуль этого вектора часто называют градиентом, который определяется следующим образом:

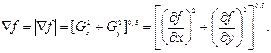
В силу большего объема вычислений, необходимых для обработки всего изображения оператором градиента, на практике часто используют приближенное значение в виде:

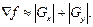
Определим дискретные приближения приведенных уравнений. Для указания пикселей в окрестности 3×3 будем использовать обозначения, представленные на рисунке 1.5.

Рисунок 1.5 – Область изображения размером 3×3 элемента

Простейшими приближениями первой производной являются следующие выражения: G_x = z ₈ – z ₅ и G_y = z ₆ – z ₅. Робертс предложил использовать перекрестные направления: G_x = z ₉ – z ₅ и G_y = z ₈ – z ₆. В этом случае градиент будет определяться следующим выражением:

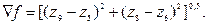
В случае использования приближенной формулы для определения градиента:

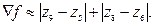
Приведенное уравнение может быть реализовано с помощью масок, приведенных на рисунке 1.6.

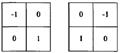
Рисунок 1.6 – Маски 2×2, используемые для вычисления

градиента

Данные маски называют перекрестным градиентным оператором Робертса. Однако маски четного размера неудобны в своей реализации, поэтому более предпочтительным является применение масок с минимальным размером окрестности 3×3, в этом случае градиентный оператор может быть реализован с помощью следующего выражения:

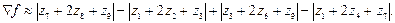
Соответствующие маски приведены на рисунке 1.7. Представленные маски называют оператором Собела.

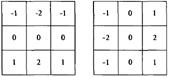
Рисунок 1.7 – Маски 3×3, используемые для вычисления

градиента

Использование весовых коэффициентов со значением 2 основано на стремлении присвоить центральным точкам большую значимость и тем самым достичь большей гладкости. Заметим, что сумма коэффициентов каждой из масок равна нулю, что обеспечивает нулевой отклик операторов первой производной на участках изображения с постоянным уровнем яркости, что соответствует требованиям к оператору первой производной. Градиентные операторы применяются для улучшения контуров, в задачах улучшения видимости дефектов и для удаления слабо меняющихся характеристик фона.

Комбинированные методы пространственного

Улучшения изображений

При решении конкретных задач обработки биомедицинских изображений для достижения приемлемого результат может потребоваться применение нескольких дополняющих друг друга пространственных методов улучшения изображения.

В клинической диагностике используются полные снимки скелета, полученные с помощью гамма-лучей для обнаружения таких заболеваний, как костные инфекции и опухоли. Одной из актуальных задач обработки такого рода изображений является повышение резкости изображения для более подробного выявления деталей скелета. Зачастую такие изображения характеризуются малым динамическим диапазоном уровней яркости и высоким содержанием шума, что затрудняет реализацию поставленных задач.

Стратегия обработки данного вида изображений состоит в использовании лапласиана для выделения мелких деталей скелета и градиента для улучшения выступающих краев, а также градационного преобразования для увеличения динамического диапазона яркостей.

Альтернативным подходом является использование маски, формируемой путем сглаживания градиента исходного изображения. Оператор второй производной (лапласиан) обеспечивает значительное улучшение отображения мелких деталей изображения, по сравнению с градиентом, однако, при этом лапласиан усиливает шум в большей степени, чем градиент. Градиент по сравнению с лапласианом дает более сильный отклик в областях со значительными изменениями яркости (яркостные переходы и ступеньки), при этом отклик градиента на шум и мелкие детали слабее, чем у лапласиана, и может быть в дальнейшем дополнительно снижен путем сглаживания градиента усредняющим фильтром.