В данном случае рассматривается использование оператора двумерной второй производной в задачах улучшения изображения. Подход сводится к выбору дискретной формулировки второй производной и к последующему построению маски фильтра, основанной на предложенной формулировке. В данных задачах рассматриваются исключительно изотропные фильтры, отклик которых не зависит от направления неоднородностей на обрабатываемом изображении. Изотропные фильтры обладают свойством инвариантности к повороту изображения, то есть поворот изображения и последующее применение фильтра дает тот же результат, что и первоначальное применение фильтра с последующим поворотом результата.

Простейшим оператором, основанным на производных, является оператор Лапласа – лапласиан, который для функции двух переменных определяется как:

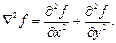
Для применения оператора Лапласа в цифровой обработке изображений его необходимо выразить в дискретном виде. Наиболее часто используется следующее представление:

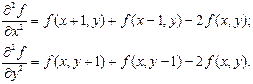
Дискретная формулировка двумерного лапласиана получается объединением этих двух составляющих:

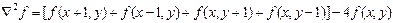
Данное уравнение может быть реализовано с помощью маски, представленной на рисунке 1.3.

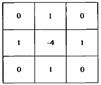
Рисунок 1.3 – Маска фильтра, используемая для реализации дискретного лапласиана

Данная маска дает изотропный результат для поворотов на углы, кратные 90⁰. В формулу дискретного лапласиана могут быть включены диагональные направления добавлением еще двух членов – по одному для каждого из диагональных направлений. Маска, соответствующая такому определению, представлена на рисунке 1.4.

Рисунок 1.4 – Маска фильтра, используемая для реализации

дискретного лапласиана и полученная с учетом диагональных направлений

Данная маска является изотропной для поворотов на углы, кратные 45⁰.

В силу того, что оператор Лапласа по сути является второй производной, его применение подчеркивает разрывы уровней яркостей на изображении и подавляет области со слабыми изменениями яркостей. Это приводит к получению изображения, содержащего сероватые линии на месте контуров и других разрывов, наложенные на темный фон без особенностей. Для восстановления прежнего фона при сохранении эффекта повышения резкости, достигаемого использованием лапласиана, достаточно сложить исходное изображение и изображение, получаемое на выходе оператора Лапласа.

Необходимо отметить, что результаты, получаемые с применением маски, содержащей диагональные элементы (рисунок 1.4), являются более резкими, чем с применением первичной маски, приведенной на рисунке 1.3.