Шаг 1: Считывание изображения
Считаем файл hestain.png, который содержит изображение гемотоксина и эозина (H&E). Здесь применен метод окрашивания для детального анализа патологий (рисунок 3.1).
he=imread('hestain.png');
imshow(he), title('H&E изображение');
text(size(he, 2),size(he, 1)+15,...
'Image courtesy of Alan Partin, Johns Hopkins University',...'FontSize',7,
'HorizontalAlignment', 'right');
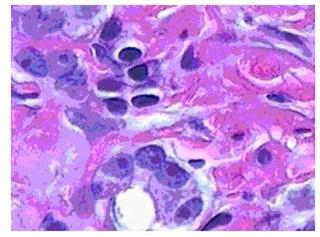
Рисунок 3.1 – Окрашенные гемотоксин и эозин
Шаг 2: Преобразование изображения из цветовой системы RGB в цветовую систему L*a*b*
Какое количество цветов видно на изображении 22, если не принимать во внимание возможность комбинации яркостей? На самом деле таких цветов три: белый, голубой и розовый. Следует отметить различия этих цветов между собой. Цветовое пространство L*a*b* (оно также известно как CIELAB или CIE L*a*b*) дает возможность различать эти визуальные различия. Цветовое пространство L*a*b* получено на основе трехцветных значений CIE XYZ. Пространство L*a*b* включает информацию о значении интенсивности 'L*', значении цветности 'a*', которое показывает какой цвет выбран на красно-зеленой оси и значение цветности 'b*' показывает какой цвет выбран на голубо-желтой оси. Вся информация о цветах содержится в значениях 'a*' и 'b*'. Оценить разницу между двумя цветами можно с использованием евклидового расстояния. Преобразуем изображение в цветовое пространство L*a*b* с использованием функций makecform и applycform.
cform=makecform('srgb2lab');
lab_he=applycform(he, cform);
Шаг 3: Классификация цветов в пространстве 'a*b*' с использованием кластеризации (метод k-средних)
Кластеризация приводит к разделению объектов на группы. Кластеризация методом k-средних приводит также к локализации объектов в пространстве. Поиск разделения, т.е. того, какой объект к какому классу принадлежит, происходит на основе анализа метрического расстояния между объектами. Далее на основании информации о цветах в пространстве 'a*b*', каждому пикселю объекта присваивается значение 'a*' и 'b*'. Используем кластеризацию методом k-средних для разделения объектов на три кластера. Для этого используем евклидовую метрику.
ab=double(lab_he(:, :, 2:3));
nrows=size(ab, 1);
ncols=size(ab, 2);
ab=reshape(ab, nrows*ncols, 2);
nColors=3;
[cluster_idx cluster_center]=kmeans(ab, nColors, 'distance', 'sqEuclidean', ...
'Replicates',3);
Шаг 4: Присвоение меток каждому пикселю изображения на основе метода k-средних
Для каждого объекта на исходном изображении метод k-средних возвращает индекс соответствующего кластера. Значение параметра cluster_center, которое получено в результате применения метода k-средних будет использовано при дальнейшей демонстрации метода. Отметим пиксели, которые содержатся в cluster_index.
pixel_labels=reshape(cluster_idx, nrows,ncols);
imshow(pixel_labels, []), title ('изображение, отмеченное кластерными индексами');
Изображение, отмеченное кластерными индексами, представлено на рисунке 3.2.

Рисунок 3.2 – Изображение, отмеченное кластерными
индексами
Шаг 5: Создание сегментированного изображения на основе цветного
Используя параметр pixel_labels, можно разделить объекты на изображении hestain.png по цветам (рисунки 3.3, 3.4, 3.5).
segmented_images=cell(1, 3);
rgb_label=repmat(pixel_labels, [1 1 3]);
for k=1 : nColors
color=he;
color(rgb_label~=k)=0;
segmented_images{k}=color;
end
imshow(segmented_images{1}), title('объекты в кластере 1');
imshow(segmented_images{2}), title('объекты в кластере 2');
imshow(segmented_images{3}), title('объекты в кластере 3');
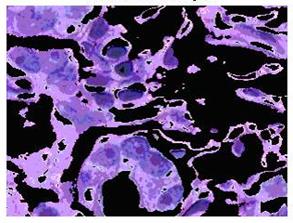
Рисунок 3.3 – Объекты в кластере 1
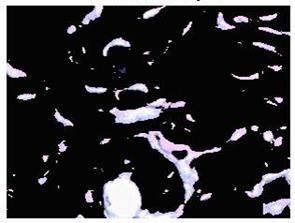
Рисунок 3.4 – Объекты в кластере 2
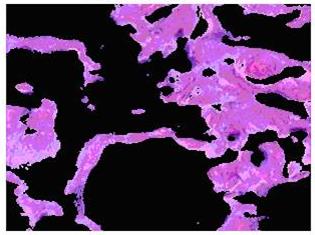
Рисунок 3.5 – Объекты в кластере 3
Шаг 6: Сегментация ядер на основании отдельного изображения
Рассмотрим изображение, которое содержит синие объекты (рисунок 3.3). Отметим, что они являются темно-синими и светло-синими. Используя значение 'L*' в цветовом пространстве L*a*b*, можно отделить темно-синие объекты от светло-синих. Напомним, что параметр 'L*' содержит значения интенсивностей для каждого цвета. Найдем кластеры, которые содержат синие объекты. Получим значения интенсивностей объектов в этом кластере и обработаем их пороговым методом с использованием функции im2bw. Параметр cluster_center содержит среднее значение 'a*' и 'b*' для каждого кластера. Синий кластер имеет второе наибольшее значение cluster_center.
mean_cluster_val=zeros(3, 1);
for k=1:nColors
mean_cluster_val(k)=mean(cluster_center(k));
end
[mean_cluster_val,idx]=sort(mean_cluster_val);
blue_cluster_num=idx(2);
L=lab_he(:, :, 1);
blue_idx=find(pixel_labels==blue_cluster_num);
L_blue=L(blue_idx);
is_light_blue=im2bw(L_blue,graythresh(L_blue));
Используем маску is_light_blue для того, чтобы пометить те пиксели, которые являются частью синего ядра. Отобразим синие ядра на разделенном изображении (рисунок 3.6).
nuclei_labels=repmat(uint8(0), [nrows ncols]);
nuclei_labels(blue_idx(is_light_blue==false))=1;
nuclei_labels=repmat(nuclei_labels, [1 1 3]);
blue_nuclei=he;
blue_nuclei(nuclei_labels~=1)=0;
imshow(blue_nuclei), title('синие ядра');
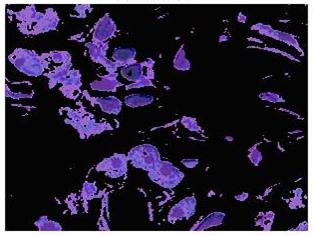
Рисунок 3.6 – Синие ядра в кластере 1
2.2 Задания для самостоятельной работы
Получить от преподавателя адрес нескольких (на усмотрение преподавателя) биомедицинских изображений и проведите процедуру сегментации, описанную в п. 2.1. Выписать и прокомментировать все изменения исходного кода.
СОДЕРЖАНИЕ ОТЧЕТА
1. Цель работы.
2. Листинги написанных программ (M-файлов) в среде MATLAB для каждого задания.
3. Сводная таблица результатов, содержащая полученные в результате проведенных исследований изображения в сравнении с исходными изображениями.
4. Выводы о полученных результатах, сопоставление с теорией.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Определение и цель сегментации.
2. В чем заключается результат сегментации?
3. Назовите основные практические применения сегментации.
4. В чем состоит основная сложность при сегментации биомедицинских изображений?
5. Что такое кластеризация?
6. Какое цветовое пространство использовалось в данной лабораторной работе? В чем его принципиальное отличие от RGB?
7. Как оценивается разница между цветами в данной лабораторной работе?
8. Метод k-средних. Принципы, алгоритм, применение.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Журавель И.М. Краткий курс теории обработки изображений. М., 1999.
2. Шапиро Л., Стокман Дж. Компьютерное зрение. М.: Бином. Лаборатория знаний, 2006. 752 с.
3. Дьяконов В., Круглов В. Математические пакеты расширения MatLAB. Специальный справочник. СПб: Питер, 2001. 488 с.
ЛАБОРАТОНАЯ РАБОТА №4
«РАСПОЗНАВАНИЕ ОБРАЗОВ»
Цель работы: получить практические навыки по работе с алгоритмами распознавания образов в среде MATLAB для решения простых технических задач искусственного интеллекта.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Распознавание образов — это отнесение исходных данных к определенному классу с помощью выделения существенных признаков, характеризующих эти данные, из общей массы несущественных данных.
При постановке задач распознавания стараются пользоваться математическим языком, стремясь - в отличие от теории искусственных нейронных сетей, где основой является получение результата путем эксперимента, - заменить эксперимент логическими рассуждениями и математическими доказательствами.
Классическая постановка задачи распознавания образов:
Дано множество объектов. Относительно них необходимо провести классификацию. Множество представлено подмножествами, которые называются классами.
Заданы: информация о классах, описание всего множества и описание информации об объекте, принадлежность которого к определенному классу неизвестна.
Требуется по имеющейся информации о классах и описании объекта установить - к какому классу относится этот объект.
Наиболее часто в задачах распознавания образов рассматриваются монохромные изображения, что дает возможность рассматривать изображение как функцию на плоскости. Если рассмотреть точечное множество на плоскости T, где функция f (x, y) выражает в каждой точке изображения его характеристику — яркость, прозрачность, оптическую плотность, то такая функция есть формальная запись изображения.
Множество же всех возможных функций f(x, y) на плоскости T — есть модель множества всех изображений X. Вводя понятие сходства между образами можно поставить задачу распознавания. Конкретный вид такой постановки сильно зависит от последующих этапов при распознавании в соответствии с тем или иным подходом.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Дата: 2019-02-02, просмотров: 785.