Для выполнения прямого преобразования Фурье в пакете MATLAB используется функция fft 2, которая имеет следующий синтаксис:
F = fft 2( f )
где f – исходное изображение, F – преобразование Фурье двумерной функции f ( x , y ).
Для получения спектра изображения необходимо выполнить следующую команду:
S = abs ( F )
Команда abs вычисляет абсолютную величину (модуль) комплексной функции F.
Для смещения начала координат Фурье-преобразования в центр частотной области используется функция fftshift со следующим синтаксисом:
Fc = fftshift ( F ) ,
где Fc – центрированное Фурье-преобразование.
В силу того, что динамический диапазон изображения Фурье-преобразования очень широкий необходимо выполнять операции преобразования диапазона яркости для корректного отображения Фурье-преобразования на дисплее. Данную операцию можно выполнить с помощью логарифмического преобразования следующим образом:
S 2= log (1+ abs ( Fc )).
Обратное преобразование Фурье выполняется с помощью функции ifft 2, которая имеет следующий синтаксис:
f = ifft 2( F ) ,
где F – преобразование Фурье, f – соответствующее изображение.
После выполнения обратного Фурье-преобразования необходимо выделить вещественную часть результата с помощью команды следующего вида:
f = real ( ifft 2( F )) .
В среде MATLAB существуют специальные функции для составления матриц и векторов. Простейшим способом задать одномерный массив (вектор) является запись команды следующего вида:
[ name ]= X 1: dX : Xk ,
где name – имя переменной, которое будет присвоено сформированному массиву, X 1 – значение первого элемента массива, Xk – значение последнего элемента, dX – шаг с помощью которого формируется каждый следующий элемент (по умолчанию равен 1). Данная запись формирует вектор-строку. Для того, чтобы сформировать вектор-столбец необходимо использовать следующую запись:
[name]=[X1:dX:Xk]’,
где символ ’ обозначает транспонирование матрицы.
При решении задач цифровой обработки изображений необходимо формировать двумерные массивы координатной сетки. С этой целью в системе MATLAB удобно использовать функцию meshgrid, которая формирует выходные массивы, определяющие координаты узлов прямоугольника, задаваемого входными векторами. Формируемый прямоугольник задает область определения функции от двух переменных. Функция meshgrid имеет следующий синтаксис:
[X, Y]=meshgrid(x, y).
Строки матрицы X являются копиями вектора x, а столбцы матрицы Y – копиями вектора y. Формирование таких массивов упрощает вычисление функций двух переменных, позволяя применять операции над массивами. Пример: пусть x =(0, 1, 2) y =(0, 1). Тогда 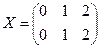 ,
, 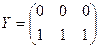 .
.
Формирование таких массивов упрощает вычисление функций двух переменных, позволяя применять операции над массивами.
Таким образом, для осуществления частотной фильтрации исходного изображения f(x, y) необходимо выполнить следующую последовательность операций:
1) определить размеры изображения f(x, y) с помощью команды size; сформировать векторы частотных координат u и v размеры которых, равны размерам векторов соответствующих пространственных координат x и y;
2) выполнить прямое преобразование Фурье исходного изображения с помощью команды fft 2 и получить частотное представление F(u, v);
3) задать значение частоты среза в пикселях (как правило, определяется единицами процентов от максимального горизонтального или вертикального размера изображения); сформировать передаточную характеристику требуемого фильтра H(u, v), представляющую собой двумерную матрицу, размеры которой совпадают с размерами матрицы исходного изображения;
4) получить частотное представление отфильтрованного изображения G(u, v) путем выполнения операции поэлементного умножения передаточной характеристики фильтра H(u, v) и Фурье преобразования исходного изображения F(u, v);
5) получить пространственное представление отфильтрованного изображения g(x, y) путем выполнения процедуры обратного преобразования Фурье от частотного представления G(u, v) с помощью команды ifft 2.
6) Выделить вещественную часть результата, полученного на предыдущем этапе с помощью команды real.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Загрузите изображение рентгеновского снимка грудной клетки xraychest . jpg. Выполните Фурье-преобразование исходного изображения, получите изображение спектра в частотной области. Для улучшения визуального восприятия воспользуйтесь градационным логарифмическим преобразованием.
2. Примените методику высокочастотной фильтрации с подъемом частотной характеристики исходного изображения рентгеновского снимка грудной клетки xraychest . jpg.
2.1. Выполните операцию низкочастотной фильтрации исходного изображения рентгеновского снимка грудной клетки xraychest . jpg.
2.2. Подбором параметра A добейтесь наилучшего результата повышения резкости с помощью подъема частотной характеристики.
2.3. Изображение, полученное в результате выполнения пункта 2.2, подвергните процедуре гистограммной эквализации. Для получения справочной информации системы MATLAB по выполнению данной процедуры используйте команду doc histeq.
3. Примените методику фильтрации с усилением высоких частот к исходному изображению рентгеновского снимка грудной клетки xraychest . jpg с целью повышения резкости изображения.
3.1. Выполните операцию высокочастотной фильтрации исходного изображения рентгеновского снимка грудной клетки xraychest . jpg.
3.2. Подбором параметров a и b добейтесь усиления высоких частот.
3.3. Изображение, полученное в результате выполнения пункта 3.2, подвергните процедуре гистограммной эквализации.
4. Сравните изображения, полученные в результате выполнения второго и третьего пунктов задания. Сделайте выводы о полученных результатах.
СОДЕРЖАНИЕ ОТЧЕТА
1. Цель работы.
2. Листинги написанных программ (M-файлов) в среде MATLAB для каждого задания.
3. Сводная таблица результатов, содержащая полученные в результате проведенных исследований изображения в сравнении с исходными изображениями.
4. Выводы о полученных результатах, сопоставление с теорией.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Двумерное Фурье-преобразование изображений.
2. Основы частотной фильтрации изображений.
3. Сглаживающие частотные фильтры.
4. Частотные фильтры повышения резкости.
5. Нерезкое маскирование. Высокочастотная фильтрация с подъемом частотной характеристики.
6. Фильтрация с усилением высоких частот.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Гонсалес, Р. Цифровая обработка изображений [Текст] / Р. Гонсалес, Р. Вудс. – М.: Техносфера, 2006. – 1072 с.
2. Гонсалес, Р. Цифровая обработка изображений в среде Matlab [Текст] / Р. Гонсалес, Р. Вудс, С. Эддинс. – М.: Техносфера, 2006. – 616 с.
3. Алексеев, Е.Р. MATLAB 7 [Текст] / Алексеев Е.Р., Чеснокова О.В. – М.: NT Press, 2006. – 464 с.
ЛАБОРАТОРНАЯ РАБОТА №3
«СЕГМЕНТАЦИЯ БИОМЕДИЦИН
СКИХ ИЗОБРАЖЕНИЙ»
Цель работы: получить практические навыки сегментации биомедицинских изображений в системе компьютерных вычислений Matlab.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
В компьютерном зрении сегментация – это процесс разделения цифрового изображения на несколько сегментов (множество пикселей, также называемых суперпикселями). Цель сегментации заключается в упрощении и/или изменении представления изображения, чтобы его было легче анализировать. Сегментация изображений обычно используется для того, чтобы выделить объекты и границы (линии, кривые, и т. д.) на изображениях. Другими словами, сегментация изображений — это процесс присвоения таких меток каждому пикселю изображения таким образом, что пиксели с одинаковыми метками имеют общие визуальные характеристики.
Результатом сегментации изображения является множество сегментов, которые вместе покрывают всё изображение, или множество контуров, выделенных из изображения. Все пиксели в сегменте похожи по некоторой характеристике или вычисленному свойству, например, по цвету, яркости или текстуре. Соседние сегменты значительно отличаются по этой характеристике.
Некоторыми практическими применениями сегментации изображений являются:
- медицинские изображения;
- обнаружение опухолей и других патологий;
- определение объёмов тканей;
- хирургия при помощи компьютера;
- диагностика;
- планирование лечения;
- изучение анатомической структуры;
- выделение объектов на спутниковых снимках;
- распознавание лиц;
- распознавание отпечатков пальцев;
- системы управления дорожным движением;
- обнаружение стоп-сигналов;
- машинное зрение.
Для сегментации изображений было разработано несколько универсальных алгоритмов и методов. Так как общего решения для задачи сегментации изображений не существует, часто эти методы приходится совмещать со знаниями из предметной области, чтобы эффективно решать эту задачу в её предметной области.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Дата: 2019-02-02, просмотров: 794.