Признаков
Каждый объект можно охарактеризовать набором некоторых признаков. Количество признаков зависит от сложности самого объекта. Точность подбора признаков будет влиять на эффективность распознавания объекта, который описывается этим набором.
Рассмотрим пример распознавания простых объектов на основе набора признаков. При реализации метода в качестве основных будем использовать две функции bwlabel и imfeature, которые встроены в приложение Image Processing Toolbox.
Сначала считаем исходное тестовое изображение в рабочее пространство MATLAB (местоположение необходимо уточнить у преподавателя) и визуализируем его.
L=imread('test_image.bmp');
figure, imshow(L);
Сделаем некоторые замечания относительно исходного изображения. В нашем случае исходные данные представлены бинарным изображением (рисунок 4.1). Это несколько упрощает нашу задачу, поскольку основной акцент в этом примере сделан на распознавание объектов.
Рисунок 4.1 – Исходное тестовое изображение
Однако при решении задач распознавания на основе реальных изображений, в большинстве случаев, важной является задача преобразования исходного изображения в бинарное. Качество решения этой задачи во многом определяет эффективность дальнейшего распознавания.
Функции bwlabel и imfeature в качестве исходных данных используют полутоновые двумерные изображения. Поскольку изображение test_image.bmp было сформировано как бинарное, но сохранено в формате bmp, то из трехмерной матрицы изображения L, которая содержит три идентичных цветовых шара, необходимо выделить один из шаров, например, первый.
L=L(:,:,1);
Такого же результата можно достичь, используя функцию rgb2gray. Таким образом, матрица L представляет бинарное двумерное изображение. Для дальнейших расчетов определим размеры этого изображения
[N,M]=size(L);
Далее необходимо локализировать, т.е. определить расположение объектов на изображении. Для этого будем использовать функцию bwlabel, которая ищет на бинарном изображении связные области пикселей объектов и создает матрицу, каждый элемент которой равен номеру объекта, которому принадлежит соответствующий пиксель исходного изображения. Параметр num дополнительно возвращает количество объектов, найденных на исходном бинарном изображении.
[L num]=bwlabel(L,8);
Кроме того, в функции bwlabel указывается еще один параметр – значение связности.
Далее приступаем к вычислению признаков объектов, которые отмечены в матрице номеров объектов L. Рассмотрим этот вопрос более подробно. Значения признаков возвращаются в массиве структур feats. Как было отмечено ранее, при распознавании объектов могут использоваться любые наборы признаков.
В рамках этого примера применим наиболее наглядный статистический подход к классификации объектов на основе морфометрических признаков. К основным морфометрическим признакам относятся коэффициенты формы:
‘solidity’ – коэффициент выпуклости: равен отношению площади к выпуклой площади объекта; представляется числом в диапазоне (0,1];
‘extent’ – коэффициент заполнения: равен отношению площади объекта к площади ограничивающего прямоугольника; представляется числом в диапазоне (0,1];
‘eccentricity’ – эксцентриситет эллипса с главными моментами инерции, равными главным моментам инерции объекта; представляется числом в диапазоне (0,1].
Поскольку в данном примере используется тестовое изображение объектов простой формы, то из перечисленных признаков в программной реализации будем использовать только коэффициент заполнения ‘extent’. Как было сказана ранее, параметр ‘extent’ определяется отношением площади объекта к площади ограничивающего прямоугольника. Для круга этот параметр будет равен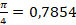 
, а для квадрата – 1. Но эти данные приведены для случая, когда круг и квадрат имеют идеальную форму. Если форма круга или квадрата искажена, то значения параметра ‘extent’ также могут отличаться от приведенных выше значений. Поэтому коэффициенты формы могут вычисляться с некоторой погрешностью. Таким образом, вводя некоторую погрешность в коэффициент формы, допускаются некоторые ее искажения. Причем значение погрешности пропорционально степени искажения. Однако слишком большое значение погрешности может привести к неправильному распознаванию объектов.
Дополнительно также будем определять центр масс объекта с помощью опции ‘centroid’.
feats=imfeature(L,'Centroid','Extent',8);
Перепишем значения признаков из массива структур feats в отдельные массивы.
Extent=zeros(num);
CentX=zeros(num);
CentY=zeros(num);
for i=1:1:num;
Extent(i)=feats(i).Extent;
CentX(i)=feats(i).Centroid(1);
CentY(i)=feats(i).Centroid(2);
end;
Также в рамках этого примера реализуем следующее. Для наглядности, каждый распознанный объект будет подписан. Для реализации этого возможны различные подходы. Один самых простых – это помещать около распознанного объекта изображение с его названием. Для этого прежде нужно сформировать изображения с названиями объектов и считать их в рабочее пространство MATLAB. Поскольку на тестовом изображении присутствуют только круги и квадраты, то сформирует и считаем соответствующие изображения (рисунок 4.2).
Krug=imread('krug.bmp');
Kvadrat=imread('kvadrat.bmp');
d=0.15; % погрешность коэффициента формы
for i=1:num
L(round(CentY(i)):round(CentY(i))+1,round(CentX(i)):round(CentX(i))+1)=0;
if (abs(Extent(i)-0.7822)<d)==1
L(round(CentY(i)):round(CentY(i))+24,round(CentX(i)):round(CentX(i))+44)=Krug;
end;
if ( abs(Extent(i)-1)<d)==1;
L(round(CentY(i)):round(CentY(i))+24,round(CentX(i)):round(CentX(i))+44)=Kvadrat;
end;
end;
figure, imshow(L);
Рисунок 4.2 – Результат распознавания
Существуют также другие подходы к распознаванию объектов на основе набора признаков. Они различны по своей вычислительной сложности, эффективности и т.п.
2.2 Задания для самостоятельной работы
Получить от преподавателя адрес биомедицинского изображения и выполнить следующие задания:
1. Отфильтровать шумы для достижения приемлемого качества изображения.
2. Изменить код программы для достижения распознавания простейших примитивов на биомедицинском изображении.
СОДЕРЖАНИЕ ОТЧЕТА
1. Цель работы.
2. Листинги написанных программ (M-файлов) в среде MATLAB для каждого задания.
3. Сводная таблица результатов, содержащая полученные в результате проведенных исследований изображения в сравнении с исходными изображениями.
4. Выводы о полученных результатах, сопоставление с теорией.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В чем заключается распознавание образов?
2. Что такое признаки в контексте задачи распознавания образов?
3. Классическая постановка задачи распознавания образов.
4. Сформулируйте основную задачу распознавания для вашего изображения (индивидуального задания).
5. Какая основная задача возникает при распознавании реальных изображений? Как ее можно решить?
6. Какие признаки используются для классификации в данной лабораторной работе?
7. С какой целью в коэффициент формы вводится погрешность?
3. Какие внешние условия могут повлиять на качество распознавания вашего изображения (индивидуального задания)?
4. Опишите весь цикл процедуры распознавания.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Журавель И.М. Краткий курс теории обработки изображений. М., 1999.
2. Шапиро Л., Стокман Дж. Компьютерное зрение. М.: Бином. Лаборатория знаний, 2006. 752 с.
3. Дьяконов В., Круглов В. Математические пакеты расширения MatLAB. Специальный справочник. СПб: Питер, 2001. 488 с.
ЛАБОРАТОРНАЯ РАБОТА №5
«НЕЙРОННЫЕ СЕТИ»
Цель работы: получить практические навыки по работе с нейронными сетями в среде MATLAB для решения простых технических задач искусственного интеллекта.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Введение в нейронные сети
В последнее время наблюдается сильный интерес к нейронным системам, которые сегодня уже нашли применение в разнообразных сферах человеческой деятельности: медицине, бизнесе, технике. Нейронные сети используют для решения задач управления, классификации, прогнозирования. Такой успех определяется следующими причинами.
Нейросети – это мощнейший метод имитации явлений и процессов, который позволяет показывать сложнейшие зависимости. Нейронные сети являются нелинейными по своей природе, в то же время как на протяжении нескольких лет для создания моделей применялся линейный подход. А также, во многих случаях нейронные сети помогали преодолеть, так называемое, «проклятие размерности», которая обусловлена тем, что создание модели нелинейных явлений требует большого количества вычислительных ресурсов (в случае большого числа переменных).
Следующая особенность нейросетей связана с тем, что используется механизм обучения. Пользователь нейронной системы подбирает представительные данные и запускает обучающий алгоритм, который сам настраивает параметры сети без участия пользователя. От пользователя только требуется набор эвристических знаний о том, как следует подготавливать и отбирать данные, выбирать необходимую архитектуру нейронной сети и интерпретировать полученные результаты. Однако следует заметить, что уровень знаний, требующийся от пользователя, который необходим для успешного применения нейронной системы, намного меньше, чем, к примеру, при использовании традиционных методов.
Дата: 2019-02-02, просмотров: 477.
