ОСНОВНЫЕ ПРИЕМЫ РАБОТЫ В СРЕДЕ MATLAB
Язык MATLAB является высокоуровневым языком программирования, включающим основанные на матрицах структуры данных, широкий спектр функций, интегрированную среду разработки, объектно-ориентированные возможности и интерфейсы к программам, написанным на других языках программирования.
Основной особенностью языка MATLAB является его широкие возможности по работе с матрицами. MATLAB предоставляет пользователю большое количество (несколько сотен) функций для анализа данных, покрывающие практически все области математики, в частности, система MATLAB предоставляет пользователю многофункциональную и эффективную среду цифровой обработки двумерных изображений: Image Processing Toolbox. Это специальный набор инструментов, расширяющий базовую функциональность среды MATLAB. Image Processing Toobox представляют собой коллекции функций, написанных на языке MATLAB для решения широкого круга задач цифровой обработки изображений.
Рабочий стол MATLAB
На рисунке В.1 приведен рабочий стол в среде MATLAB, содержащий четыре подокна: окно команд (Command Window), окно рабочего пространства (Workspace Browser), окно текущей папки (Current Directory Window), окно совершенных команд (Comand History Window). Окно команд (Command Window) – это область, где пользователь вводит команды и выражения на языке программирования среды MATLAB и где система размещает свои ответы на пользовательские команды. При каждом сеансе работы среда MATLAB формирует рабочее пространство, т.е. множество переменных, создаваемых пользователем. Окно рабочего пространства (Workspace Browser) отображает эти переменные и информацию о них – размер и тип переменной. Окно совершенных команд (Comand History Window) содержит записи всех команд, которые пользователь вводил в окне команд, включая все предыдущие сеансы работы в среде MATLAB.
Вызов справки в среде MATLAB
Вызов окна справки в среде MATLAB осуществляется нажатием мышью на знак вопроса в строке инструментов рабочего стола или набором команды helpbrowser в командном окне. Справочная система организована в виде веб-обозревателя, интегрированного в рабочий стол MATLAВ, который способен отображать документы, написанные на языке HTML.
Существует другой путь получения справки по конкретной функции среды MATLAB. Для этого достаточно задать в командной строке команду doc, за которой следует поместить имя нужной функции. Справочная система среды MATLAB предоставляет пользователю исчерпывающую информацию по каждой имплементированной функции и содержит наглядные примеры использования данной функции для решения разного рода вычислительных задач.
Создание M -файлов (скриптов) в редакторе MATLAB
Редактор MATLAB является одновременно специализированным текстовым редактором для создания M-файлов и графическим отладчиком программ MATLAB. M-файл представляет собой созданный пользователем последовательный список исполняемых команд MATLAB, сохраненный на диске. M-файлы бывают двух типов: скрипты и функции. Скрипты не имеют входных и выходных аргументов, все переменные, объявленные в скрипте, становятся доступными в рабочей среде сразу после выполнения. Функции могут быть полезны при программировании собственных приложений, функции производят необходимые действия с входными аргументами, согласно составленной пользователем последовательности операций, и возвращают результат в выходных аргументах.
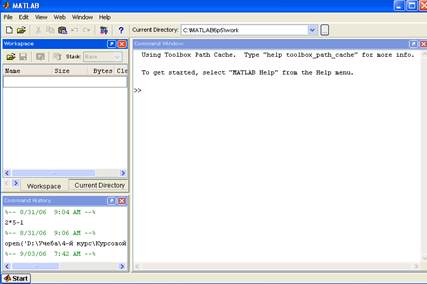
Рисунок В.1 – Рабочий стол MATLAB и его основные компоненты
Сохранение изображений
Сохранение изображений на локальный диск или внешний носитель осуществляется функцией imwrite, которая имеет следующий синтаксис:
imwrite ( f , ‘ filename ’)
Строка filename должна содержать расширение, поддерживаемое системой MATLAB, если строка filename не содержит информацию о полном пути хранения файла, то изображение записывается в файл в текущую рабочую папку, по умолчанию находящуюся в директории:
C:\Program Files/Mathworks/work
В зависимости от формата графического файла, функция imwrite может содержать дополнительный набор входных аргументов и обеспечивать большую функциональность, более подробно с особенностями работы функции можно ознакомиться в справочной системе MATLAB с помощью команды вызова справки: doc imwrite.
Преобразование яркости изображений
Функция imadjust является базовым инструментом в пакете MATLAB для преобразования яркости полутоновых изображений. Данная функция имеет следующий синтаксис:
g=imadjust(f, [low_in, high_in], [low_out, high_out], gamma)
На рисунке В.2 проиллюстрировано отображение с помощью этой функции исходного изображения f в новое изображение g, при котором значения яркости в интервале [ low _ in , high _ in ] переходят в значение интервала [ low _ out , high _ out ], а значения меньшие порога low _ in или большие порога high _ in обрезаются.
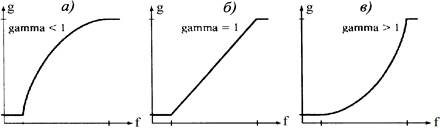
Рисунок В.2 – Различные отображения, допустимые в функции imadjust
Все входные параметры функции imadjust за исключением f являются вещественными числами в диапазоне от 0 до 1. Параметр gamma служит для задания формы кривой, отображающей яркость f в яркость g. По умолчанию параметр gamma =1, что соответствует линейному отображению.
Степенное преобразование яркости изображений или гамма-коррекция определяется с помощью следующего выражения:
S = c ∙ rγ
где r – входная (исходная) яркость, S – выходная яркость, c и γ – положительные константы.
В системе MATLAB операции возведения в степень, умножения и деления матриц при обработке соответствующих изображений необходимо выполнять поэлементно, для этого используется следующая запись команд (соответственно):
g = f .^0.5
g = f .* h
g = f ./ h
При умножении или делении матрицы на константу (скаляр) можно использовать обычную запись арифметических операций: g = f *2, g = f /2.
ЛАБОРАТОРНАЯ РАБОТА №1
«ФИЛЬТРАЦИЯ ШУМОВ НА БИОМЕДИЦИНСКИХ ИЗОБРАЖЕНИЯХ»
Цель работы: изучение методов пространственной фильтрации биомедицинских изображений с использованием возможностей пакета компьютерных вычислений MATLAB; исследование возможностей комбинированного применения различных методов линейной пространственной и методов повышения качества изображения для решения задачи обработки первичных биомедицинских изображений.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Высоких частот
Процедура, использующаяся для повышения резкости изображения, заключающаяся в вычитании из исходного изображения его расфокусированной копии называется нерезким маскированием и выражается следующей формулой:
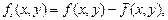
где fs(x, y) – изображение с повышенной резкостью, полученное методом нерезкого маскирования,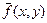 
– расфокусированная копия исходного изображения f ( x , y ).
Обобщенной операцией нерезкого маскирования является фильтрация с подъемом высоких частот, которая задается в следующем виде:
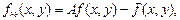
где А ≥1.
При увеличении А больше 1 эффект увеличения резкости становится меньше. Типичным применением фильтрации изображений с подъемом высоких частот является случай, когда исходное изображение темнее, чем это требуется. Варьированием постоянного коэффициента А удается добиться общего увеличения яркости изображения и получить желаемый результат.
Улучшения изображений
При решении конкретных задач обработки биомедицинских изображений для достижения приемлемого результат может потребоваться применение нескольких дополняющих друг друга пространственных методов улучшения изображения.
В клинической диагностике используются полные снимки скелета, полученные с помощью гамма-лучей для обнаружения таких заболеваний, как костные инфекции и опухоли. Одной из актуальных задач обработки такого рода изображений является повышение резкости изображения для более подробного выявления деталей скелета. Зачастую такие изображения характеризуются малым динамическим диапазоном уровней яркости и высоким содержанием шума, что затрудняет реализацию поставленных задач.
Стратегия обработки данного вида изображений состоит в использовании лапласиана для выделения мелких деталей скелета и градиента для улучшения выступающих краев, а также градационного преобразования для увеличения динамического диапазона яркостей.
Альтернативным подходом является использование маски, формируемой путем сглаживания градиента исходного изображения. Оператор второй производной (лапласиан) обеспечивает значительное улучшение отображения мелких деталей изображения, по сравнению с градиентом, однако, при этом лапласиан усиливает шум в большей степени, чем градиент. Градиент по сравнению с лапласианом дает более сильный отклик в областях со значительными изменениями яркости (яркостные переходы и ступеньки), при этом отклик градиента на шум и мелкие детали слабее, чем у лапласиана, и может быть в дальнейшем дополнительно снижен путем сглаживания градиента усредняющим фильтром.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Загрузите тестовое изображение скелета человека sceleton . jpg. Методом фильтрации с подъемом высоких частот добейтесь максимального повышение резкости исходного изображения. Для получения расфокусированного изображения используйте линейный усредняющий фильтр.
2. Примените линейную пространственную фильтрацию с помощью оператора Лапласа к исходному изображение скелета человека sceleton . jpg.
3. Сложите исходное изображение скелета человека sceleton . jpg с изображением, полученным в результате выполнения второго пункта задания.
4. Примените оператор Собела к исходному изображению скелета человека sceleton . jpg.
5. Изображение, полученное в результате выполнения четвертого пункта задания, подвергните фильтрации с помощью сглаживающего усредняющего фильтра. С помощью масок различного размера добейтесь оптимальных результатов.
6. Получите изображение путем умножения изображения, полученного после выполнения пятого пункта задания, и изображения, полученного в результате выполнения третьего пункта задания. Необходимо помнить, что речь идет о поэлементном умножении матриц изображений.
7. Получите изображения с повышенной резкостью путем сложения изображения, полученного в результате выполнения шестого пункта задания и исходного изображения изображению скелета человека sceleton . jpg.
8. Преобразуйте изображение, полученное в результате выполнения седьмого пункта задания, с помощью метода градационной коррекции по степенному закону.
9. Сравните различные методы пространственной фильтрации, использованные при выполнении всех пунктов задания. Сравните изображения, полученные в результате выполнения первого, третьего, пятого и восьмого пунктов задания. Сделайте выводы о полученных результатах.
СОДЕРЖАНИЕ ОТЧЕТА
1. Цель работы.
2. Листинги написанных программ (M-файлов) в среде MATLAB для каждого задания.
3. Сводная таблица результатов, содержащая полученные в результате проведенных исследований изображения в сравнении с исходными изображениями.
4. Выводы о полученных результатах, сопоставление с теорией.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Основной принцип метода линейной пространственной фильтрации изображений.
2. Сглаживающие линейные пространственные фильтры.
3. Пространственные фильтры повышения резкости.
4. Пространственные фильтры повышения резкости на основе второй производной.
5. Пространственные фильтры повышения резкости на основе первой производной.
6. Нерезкое маскирование и фильтрация с подъемом высоких частот.
7. Особенности применения комбинированных методов пространственной обработки биомедицинских изображений.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Гонсалес, Р. Цифровая обработка изображений [Текст] / Р. Гонсалес, Р. Вудс. – М.: Техносфера, 2006. – 1072 с.
2. Гонсалес, Р. Цифровая обработка изображений в среде Matlab [Текст] / Р. Гонсалес, Р. Вудс, С. Эддинс. – М.: Техносфера, 2006. – 616 с.
Лабораторная работа №2
«Дискретные ортогональные
преобразования»
Цель работы: изучение методов частотной фильтрации биомедицинских изображений с использованием возможностей пакета компьютерных вычислений MATLAB.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Введение в Фурье-анализ
Частотные методы улучшения изображений основаны на выполнении преобразования Фурье над функцией двух переменных – функцией дискретного изображения. Прямое дискретное Фурье-преобразование функции f(x, y), изображения размером M × N, задается равенством:
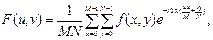
где u =0, 1, 2,…, M –1; v =0, 1, 2,…, N –1.
Обратное преобразование Фурье определяется выражением:
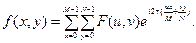
Переменные u и v называются переменными преобразования или частотными переменными, а переменные x и y называются пространственными переменными или переменными изображения. Как правило, числа M и N являются четными для упрощения компьютерной реализации, а центр Фурье образа находится в точке с координатами: u =(M /2)+1, v =(N/2)+1. Значение Фурье-преобразования в точке (u, v)=(0, 0) равно:
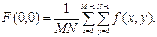
Таким образом, если f(x, y) – изображение, то значение Фурье-преобразования в начале координат равно среднему значению яркости на изображении. Поскольку началу координат отвечают нулевые частоты, то величину F(0, 0) часто называют постоянной составляющей спектра. В силу того, что функция f(x, y) вещественная, то спектр Фурье-преобразования изображения обладает свойством симметрии. Справедливы следующие соотношения между отсчетами в пространственной и частотной области:
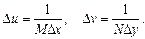
Фурье-спектр изображения состоит из пикселей, имеющих большой динамический диапазон яркости. Система воспроизведения изображений, как правило, не способна правильно отобразить столь большой диапазон значений интенсивности, что приводит к тому, что при обычном отображении спектра Фурье теряется значительное число деталей. В этой связи для улучшения зрительного восприятия полутонов, изображение спектра подвергается логарифмическому преобразованию.
На рисунке 2.1 приведено изображение, представляющее собой белый прямоугольник размерами 20×40 пикселей, наложенный на черный фон размерами 512×512 пикселей, а также представлен центрированный Фурье спектр изображения. Для того, чтобы центрировать спектр необходимо исходное изображение умножить на (–1)x+y перед вычислением Фурье-преобразования.
Рисунок 2.1 – Изображение белого прямоугольника размерами 20×40 пикселей на черном фоне размерами 512×512 пикселей (слева) и центрированный Фурье-спектр, представленный после применения логарифмического преобразования (справа)
Основы частотной фильтрации
Частотная область цифрового изображения представляет собой не что иное, как пространство, в котором принимают значения переменные (u, v) Фурье-преобразования. Как известно частота сигнала прямо связана со скоростью изменения сигнала, поэтому интуитивно понятно, что частоты в Фурье-преобразовании связаны с вариацией яркости на изображении. Наиболее медленно меняющаяся (постоянная) частотная составляющая (u=0, v=0) совпадает со средней яркостью изображения. Низкие частоты, соответствующие точкам вблизи начала координат Фурье-преобразования, определяют медленно меняющиеся компоненты изображения. По мере удаления от начала координат, более высокие частоты начинают соответствовать все более и более быстрым изменениям яркости, представляющие собой границы объектов и другие детали изображения, характеризующиеся резкими изменениями яркости, например, шум на изображении.
Процедура фильтрации изображения в частотной области состоит из следующих шагов:
1. Исходное изображение умножается на (–1)x+y, чтобы его Фурье преобразование оказалось центрированным.
2. Вычисляется прямое дискретное преобразование Фурье (ДПФ) F(u, v) исходного изображения.
3. Функция F(u, v) умножается на функцию фильтра H(u, v).
4. Вычисляется обратное ДПФ от результата шага 3.
5. Выделяется вещественная часть результата шага 4.
6. Результат шага 5 умножается на (–1)x+y.
Функция фильтра H(u, v) или передаточная характеристика фильтра подавляет некоторые частоты преобразования, оставляя другие при этом без изменения. На рисунке 2.2 представлена структурная схема, включающая основные этапы проведения фильтрации изображения в частотной области.
На стадии предварительной обработки помимо умножения изображения на (-1)x+y, могут применяться операции яркостного масштабирования, нормировка размеров исходного изображения, преобразование формата входных данных в формат с плавающей точкой и ряд других.
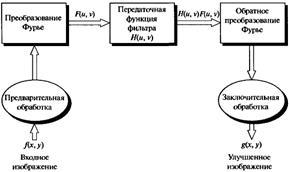
Рисунок 2.2 – Основные этапы фильтрации изображения в частотной области
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Загрузите изображение рентгеновского снимка грудной клетки xraychest . jpg. Выполните Фурье-преобразование исходного изображения, получите изображение спектра в частотной области. Для улучшения визуального восприятия воспользуйтесь градационным логарифмическим преобразованием.
2. Примените методику высокочастотной фильтрации с подъемом частотной характеристики исходного изображения рентгеновского снимка грудной клетки xraychest . jpg.
2.1. Выполните операцию низкочастотной фильтрации исходного изображения рентгеновского снимка грудной клетки xraychest . jpg.
2.2. Подбором параметра A добейтесь наилучшего результата повышения резкости с помощью подъема частотной характеристики.
2.3. Изображение, полученное в результате выполнения пункта 2.2, подвергните процедуре гистограммной эквализации. Для получения справочной информации системы MATLAB по выполнению данной процедуры используйте команду doc histeq.
3. Примените методику фильтрации с усилением высоких частот к исходному изображению рентгеновского снимка грудной клетки xraychest . jpg с целью повышения резкости изображения.
3.1. Выполните операцию высокочастотной фильтрации исходного изображения рентгеновского снимка грудной клетки xraychest . jpg.
3.2. Подбором параметров a и b добейтесь усиления высоких частот.
3.3. Изображение, полученное в результате выполнения пункта 3.2, подвергните процедуре гистограммной эквализации.
4. Сравните изображения, полученные в результате выполнения второго и третьего пунктов задания. Сделайте выводы о полученных результатах.
СОДЕРЖАНИЕ ОТЧЕТА
1. Цель работы.
2. Листинги написанных программ (M-файлов) в среде MATLAB для каждого задания.
3. Сводная таблица результатов, содержащая полученные в результате проведенных исследований изображения в сравнении с исходными изображениями.
4. Выводы о полученных результатах, сопоставление с теорией.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Двумерное Фурье-преобразование изображений.
2. Основы частотной фильтрации изображений.
3. Сглаживающие частотные фильтры.
4. Частотные фильтры повышения резкости.
5. Нерезкое маскирование. Высокочастотная фильтрация с подъемом частотной характеристики.
6. Фильтрация с усилением высоких частот.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Гонсалес, Р. Цифровая обработка изображений [Текст] / Р. Гонсалес, Р. Вудс. – М.: Техносфера, 2006. – 1072 с.
2. Гонсалес, Р. Цифровая обработка изображений в среде Matlab [Текст] / Р. Гонсалес, Р. Вудс, С. Эддинс. – М.: Техносфера, 2006. – 616 с.
3. Алексеев, Е.Р. MATLAB 7 [Текст] / Алексеев Е.Р., Чеснокова О.В. – М.: NT Press, 2006. – 464 с.
ЛАБОРАТОРНАЯ РАБОТА №3
«СЕГМЕНТАЦИЯ БИОМЕДИЦИН
СКИХ ИЗОБРАЖЕНИЙ»
Цель работы: получить практические навыки сегментации биомедицинских изображений в системе компьютерных вычислений Matlab.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
В компьютерном зрении сегментация – это процесс разделения цифрового изображения на несколько сегментов (множество пикселей, также называемых суперпикселями). Цель сегментации заключается в упрощении и/или изменении представления изображения, чтобы его было легче анализировать. Сегментация изображений обычно используется для того, чтобы выделить объекты и границы (линии, кривые, и т. д.) на изображениях. Другими словами, сегментация изображений — это процесс присвоения таких меток каждому пикселю изображения таким образом, что пиксели с одинаковыми метками имеют общие визуальные характеристики.
Результатом сегментации изображения является множество сегментов, которые вместе покрывают всё изображение, или множество контуров, выделенных из изображения. Все пиксели в сегменте похожи по некоторой характеристике или вычисленному свойству, например, по цвету, яркости или текстуре. Соседние сегменты значительно отличаются по этой характеристике.
Некоторыми практическими применениями сегментации изображений являются:
- медицинские изображения;
- обнаружение опухолей и других патологий;
- определение объёмов тканей;
- хирургия при помощи компьютера;
- диагностика;
- планирование лечения;
- изучение анатомической структуры;
- выделение объектов на спутниковых снимках;
- распознавание лиц;
- распознавание отпечатков пальцев;
- системы управления дорожным движением;
- обнаружение стоп-сигналов;
- машинное зрение.
Для сегментации изображений было разработано несколько универсальных алгоритмов и методов. Так как общего решения для задачи сегментации изображений не существует, часто эти методы приходится совмещать со знаниями из предметной области, чтобы эффективно решать эту задачу в её предметной области.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
СОДЕРЖАНИЕ ОТЧЕТА
1. Цель работы.
2. Листинги написанных программ (M-файлов) в среде MATLAB для каждого задания.
3. Сводная таблица результатов, содержащая полученные в результате проведенных исследований изображения в сравнении с исходными изображениями.
4. Выводы о полученных результатах, сопоставление с теорией.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Определение и цель сегментации.
2. В чем заключается результат сегментации?
3. Назовите основные практические применения сегментации.
4. В чем состоит основная сложность при сегментации биомедицинских изображений?
5. Что такое кластеризация?
6. Какое цветовое пространство использовалось в данной лабораторной работе? В чем его принципиальное отличие от RGB?
7. Как оценивается разница между цветами в данной лабораторной работе?
8. Метод k-средних. Принципы, алгоритм, применение.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Журавель И.М. Краткий курс теории обработки изображений. М., 1999.
2. Шапиро Л., Стокман Дж. Компьютерное зрение. М.: Бином. Лаборатория знаний, 2006. 752 с.
3. Дьяконов В., Круглов В. Математические пакеты расширения MatLAB. Специальный справочник. СПб: Питер, 2001. 488 с.
ЛАБОРАТОНАЯ РАБОТА №4
«РАСПОЗНАВАНИЕ ОБРАЗОВ»
Цель работы: получить практические навыки по работе с алгоритмами распознавания образов в среде MATLAB для решения простых технических задач искусственного интеллекта.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Распознавание образов — это отнесение исходных данных к определенному классу с помощью выделения существенных признаков, характеризующих эти данные, из общей массы несущественных данных.
При постановке задач распознавания стараются пользоваться математическим языком, стремясь - в отличие от теории искусственных нейронных сетей, где основой является получение результата путем эксперимента, - заменить эксперимент логическими рассуждениями и математическими доказательствами.
Классическая постановка задачи распознавания образов:
Дано множество объектов. Относительно них необходимо провести классификацию. Множество представлено подмножествами, которые называются классами.
Заданы: информация о классах, описание всего множества и описание информации об объекте, принадлежность которого к определенному классу неизвестна.
Требуется по имеющейся информации о классах и описании объекта установить - к какому классу относится этот объект.
Наиболее часто в задачах распознавания образов рассматриваются монохромные изображения, что дает возможность рассматривать изображение как функцию на плоскости. Если рассмотреть точечное множество на плоскости T, где функция f (x, y) выражает в каждой точке изображения его характеристику — яркость, прозрачность, оптическую плотность, то такая функция есть формальная запись изображения.
Множество же всех возможных функций f(x, y) на плоскости T — есть модель множества всех изображений X. Вводя понятие сходства между образами можно поставить задачу распознавания. Конкретный вид такой постановки сильно зависит от последующих этапов при распознавании в соответствии с тем или иным подходом.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Признаков
Каждый объект можно охарактеризовать набором некоторых признаков. Количество признаков зависит от сложности самого объекта. Точность подбора признаков будет влиять на эффективность распознавания объекта, который описывается этим набором.
Рассмотрим пример распознавания простых объектов на основе набора признаков. При реализации метода в качестве основных будем использовать две функции bwlabel и imfeature, которые встроены в приложение Image Processing Toolbox.
Сначала считаем исходное тестовое изображение в рабочее пространство MATLAB (местоположение необходимо уточнить у преподавателя) и визуализируем его.
L=imread('test_image.bmp');
figure, imshow(L);
Сделаем некоторые замечания относительно исходного изображения. В нашем случае исходные данные представлены бинарным изображением (рисунок 4.1). Это несколько упрощает нашу задачу, поскольку основной акцент в этом примере сделан на распознавание объектов.
Рисунок 4.1 – Исходное тестовое изображение
Однако при решении задач распознавания на основе реальных изображений, в большинстве случаев, важной является задача преобразования исходного изображения в бинарное. Качество решения этой задачи во многом определяет эффективность дальнейшего распознавания.
Функции bwlabel и imfeature в качестве исходных данных используют полутоновые двумерные изображения. Поскольку изображение test_image.bmp было сформировано как бинарное, но сохранено в формате bmp, то из трехмерной матрицы изображения L, которая содержит три идентичных цветовых шара, необходимо выделить один из шаров, например, первый.
L=L(:,:,1);
Такого же результата можно достичь, используя функцию rgb2gray. Таким образом, матрица L представляет бинарное двумерное изображение. Для дальнейших расчетов определим размеры этого изображения
[N,M]=size(L);
Далее необходимо локализировать, т.е. определить расположение объектов на изображении. Для этого будем использовать функцию bwlabel, которая ищет на бинарном изображении связные области пикселей объектов и создает матрицу, каждый элемент которой равен номеру объекта, которому принадлежит соответствующий пиксель исходного изображения. Параметр num дополнительно возвращает количество объектов, найденных на исходном бинарном изображении.
[L num]=bwlabel(L,8);
Кроме того, в функции bwlabel указывается еще один параметр – значение связности.
Далее приступаем к вычислению признаков объектов, которые отмечены в матрице номеров объектов L. Рассмотрим этот вопрос более подробно. Значения признаков возвращаются в массиве структур feats. Как было отмечено ранее, при распознавании объектов могут использоваться любые наборы признаков.
В рамках этого примера применим наиболее наглядный статистический подход к классификации объектов на основе морфометрических признаков. К основным морфометрическим признакам относятся коэффициенты формы:
‘solidity’ – коэффициент выпуклости: равен отношению площади к выпуклой площади объекта; представляется числом в диапазоне (0,1];
‘extent’ – коэффициент заполнения: равен отношению площади объекта к площади ограничивающего прямоугольника; представляется числом в диапазоне (0,1];
‘eccentricity’ – эксцентриситет эллипса с главными моментами инерции, равными главным моментам инерции объекта; представляется числом в диапазоне (0,1].
Поскольку в данном примере используется тестовое изображение объектов простой формы, то из перечисленных признаков в программной реализации будем использовать только коэффициент заполнения ‘extent’. Как было сказана ранее, параметр ‘extent’ определяется отношением площади объекта к площади ограничивающего прямоугольника. Для круга этот параметр будет равен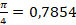 
, а для квадрата – 1. Но эти данные приведены для случая, когда круг и квадрат имеют идеальную форму. Если форма круга или квадрата искажена, то значения параметра ‘extent’ также могут отличаться от приведенных выше значений. Поэтому коэффициенты формы могут вычисляться с некоторой погрешностью. Таким образом, вводя некоторую погрешность в коэффициент формы, допускаются некоторые ее искажения. Причем значение погрешности пропорционально степени искажения. Однако слишком большое значение погрешности может привести к неправильному распознаванию объектов.
Дополнительно также будем определять центр масс объекта с помощью опции ‘centroid’.
feats=imfeature(L,'Centroid','Extent',8);
Перепишем значения признаков из массива структур feats в отдельные массивы.
Extent=zeros(num);
CentX=zeros(num);
CentY=zeros(num);
for i=1:1:num;
Extent(i)=feats(i).Extent;
CentX(i)=feats(i).Centroid(1);
CentY(i)=feats(i).Centroid(2);
end;
Также в рамках этого примера реализуем следующее. Для наглядности, каждый распознанный объект будет подписан. Для реализации этого возможны различные подходы. Один самых простых – это помещать около распознанного объекта изображение с его названием. Для этого прежде нужно сформировать изображения с названиями объектов и считать их в рабочее пространство MATLAB. Поскольку на тестовом изображении присутствуют только круги и квадраты, то сформирует и считаем соответствующие изображения (рисунок 4.2).
Krug=imread('krug.bmp');
Kvadrat=imread('kvadrat.bmp');
d=0.15; % погрешность коэффициента формы
for i=1:num
L(round(CentY(i)):round(CentY(i))+1,round(CentX(i)):round(CentX(i))+1)=0;
if (abs(Extent(i)-0.7822)<d)==1
L(round(CentY(i)):round(CentY(i))+24,round(CentX(i)):round(CentX(i))+44)=Krug;
end;
if ( abs(Extent(i)-1)<d)==1;
L(round(CentY(i)):round(CentY(i))+24,round(CentX(i)):round(CentX(i))+44)=Kvadrat;
end;
end;
figure, imshow(L);
Рисунок 4.2 – Результат распознавания
Существуют также другие подходы к распознаванию объектов на основе набора признаков. Они различны по своей вычислительной сложности, эффективности и т.п.
2.2 Задания для самостоятельной работы
Получить от преподавателя адрес биомедицинского изображения и выполнить следующие задания:
1. Отфильтровать шумы для достижения приемлемого качества изображения.
2. Изменить код программы для достижения распознавания простейших примитивов на биомедицинском изображении.
СОДЕРЖАНИЕ ОТЧЕТА
1. Цель работы.
2. Листинги написанных программ (M-файлов) в среде MATLAB для каждого задания.
3. Сводная таблица результатов, содержащая полученные в результате проведенных исследований изображения в сравнении с исходными изображениями.
4. Выводы о полученных результатах, сопоставление с теорией.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В чем заключается распознавание образов?
2. Что такое признаки в контексте задачи распознавания образов?
3. Классическая постановка задачи распознавания образов.
4. Сформулируйте основную задачу распознавания для вашего изображения (индивидуального задания).
5. Какая основная задача возникает при распознавании реальных изображений? Как ее можно решить?
6. Какие признаки используются для классификации в данной лабораторной работе?
7. С какой целью в коэффициент формы вводится погрешность?
3. Какие внешние условия могут повлиять на качество распознавания вашего изображения (индивидуального задания)?
4. Опишите весь цикл процедуры распознавания.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Журавель И.М. Краткий курс теории обработки изображений. М., 1999.
2. Шапиро Л., Стокман Дж. Компьютерное зрение. М.: Бином. Лаборатория знаний, 2006. 752 с.
3. Дьяконов В., Круглов В. Математические пакеты расширения MatLAB. Специальный справочник. СПб: Питер, 2001. 488 с.
ЛАБОРАТОРНАЯ РАБОТА №5
«НЕЙРОННЫЕ СЕТИ»
Цель работы: получить практические навыки по работе с нейронными сетями в среде MATLAB для решения простых технических задач искусственного интеллекта.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Введение в нейронные сети
В последнее время наблюдается сильный интерес к нейронным системам, которые сегодня уже нашли применение в разнообразных сферах человеческой деятельности: медицине, бизнесе, технике. Нейронные сети используют для решения задач управления, классификации, прогнозирования. Такой успех определяется следующими причинами.
Нейросети – это мощнейший метод имитации явлений и процессов, который позволяет показывать сложнейшие зависимости. Нейронные сети являются нелинейными по своей природе, в то же время как на протяжении нескольких лет для создания моделей применялся линейный подход. А также, во многих случаях нейронные сети помогали преодолеть, так называемое, «проклятие размерности», которая обусловлена тем, что создание модели нелинейных явлений требует большого количества вычислительных ресурсов (в случае большого числа переменных).
Следующая особенность нейросетей связана с тем, что используется механизм обучения. Пользователь нейронной системы подбирает представительные данные и запускает обучающий алгоритм, который сам настраивает параметры сети без участия пользователя. От пользователя только требуется набор эвристических знаний о том, как следует подготавливать и отбирать данные, выбирать необходимую архитектуру нейронной сети и интерпретировать полученные результаты. Однако следует заметить, что уровень знаний, требующийся от пользователя, который необходим для успешного применения нейронной системы, намного меньше, чем, к примеру, при использовании традиционных методов.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Динамические нейронные сети
Необходимо спроектировать динамическую линейную нейронную сеть для предсказания синусоидальной функции по четырем предшествующим значениям.
Архитектура сети: линейная нейронная сеть с линией задержки по входу на четыре такта, с одним входом, значения которого заключены в диапазоне [–1 1], и одним выходом.
Обучающая последовательность:
- входная последовательность
time = 0:0.1:10;
P = sin(time);
- последовательность целей
T = P;
Поскольку предполагается адаптивная настройка параметров сети, то обучающая последовательность должна быть представлена в виде массива ячеек:
P = con2seq(P);
T = P;
Целесообразно сформировать эти последовательности в рабочей области системы MATLAB, а затем импортировать их в рабочую область интерфейса NNTool.
Затем выберем сеть типа Linear layer (train) с линией задержки по входу (рисунок 5.8), инициализируем ее, установим начальные значения весов, выполним адаптацию сети, предварительно установив
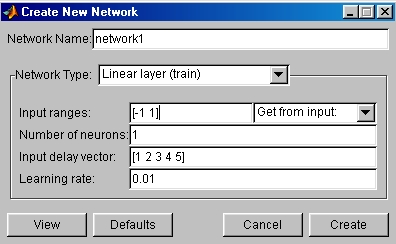
Рисунок 5.8 – Выбор типа сети
имена последовательностей входа и цели, а также указав количество циклов адаптации – 250.
По окончании проектирования экспортируем нейронную сеть в рабочую область системы MATLAB.
Теперь можно построить модель нейронной сети в системе Simulink и построить ее схему (рисунок 5.9): gensim(network1)
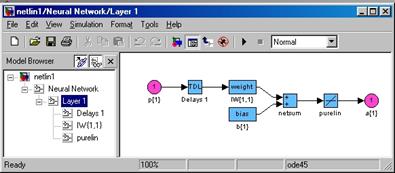
Рисунок 5.9 – Построение схемы нейронной сети
Используя описание нейронной сети, можно просмотреть веса и смещение в рабочем окне системы MATLAB:
IW = network1.IW{1,1}
IW = 0.8135 0.4798 0.1716 –0.1143 –0.3858
b = network1.b{1}
b = 0.0024
Извлечем информацию об ошибке сети и построим соответствующий график (рисунок 5.10). Обратите внимание на специальную форму применения оператора cat, которая позволяет преобразовать массив числовых ячеек в числовой массив.
E = cat(2,network1_errors{:});
plot(time(10:101), E(10:101))
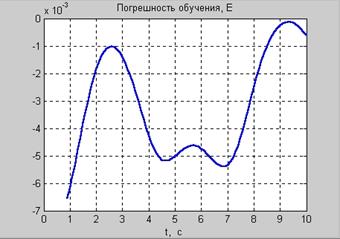
Рисунок 5.10 – График погрешности обучения
Посчитайте величины максимальной и среднеквадратичной погрешности.
Сети Кохонена
Рассмотрим самоорганизующуюся нейронную сеть с единственным слоем, задача которой заключается в том, чтобы правильно сгруппировать (кластеризировать) поступающие на нее векторы входа. Архитектура слоя Кохонена показана на рисунке 5.14.
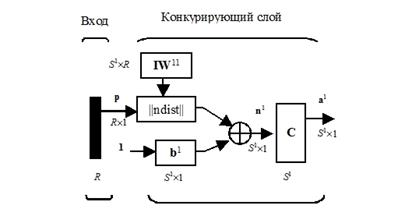
Рисунок 5.14 – Архитектура слоя Кохонена
Нетрудно убедиться, что это слой конкурирующего типа, поскольку в нем применена конкурирующая функция активации. Кроме того, архитектура этого слоя очень напоминает архитектуру скрытого слоя радиальной базисной сети. Здесь использован блок ndist для вычисления отрицательного евклидова расстояния между вектором входа p и строками матрицы весов IW11. Вход функции активации n1 – это результат суммирования вычисленного расстояния с вектором смещения b. Если все смещения нулевые, максимальное значение n1 не может превышать 0. Нулевое значение n1 возможно только в случае, когда вектор входа p оказывается равным вектору веса одного из нейронов. Если смещения отличны от 0, то возможны и положительные значения для элементов вектора n1.
Конкурирующая функция активации анализирует значения элементов вектора n1 и формирует выходы нейронов, равные 0 для всех нейронов, кроме одного нейрона – победителя, имеющего на входе максимальное значение. Таким образом, вектор выхода слоя a1 имеет единственный элемент, равный 1, который соответствует нейрону-победителю, а остальные равны 0. Такая активационная характеристика может быть описана следующим образом:
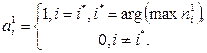
Заметим, что эта активационная характеристика устанавливается не на отдельный нейрон, а на слой. Поэтому такая активационная характеристика и получила название конкурирующей. Номер активного нейрона i* определяет ту группу (кластер), к которой наиболее близок входной вектор.
Скопируйте построчно (группами команд) и протестируйте пример, приведенный ниже.
% Этот способ обучения сети вам понадобиться, если вы не знаете цели (значение Т).
% Как видите из этого графика, система сама автоматически определила и разнесла центры кластеров.
% Также имеются параметры для тонкой настройки этой сети, их можно посмотреть при обучении сети, такие как количество эпох, градиент, погрешность и т.д.,
% к ним нужно обращаться как имя_сети.команда, например net.time
% Сеть - самоорганизующаяся сеть Кохонена
% Количество нейронов - 4
% База знаний - z
% Размерность базы знаний - 2х200
% Зададим одно из множеств значений кластера №1.
% Центром кластера будет является точка (3;0) с небольшим разбросом от центра rand(1,30) и количеством отсчетов 50.
% Т.е x1 и y1 будет являться массивом размерность 1х30
y1=0+rand(1,30)
x1=3+rand(1,30)
% посмотрим получившиеся значения (рисунок 5.15)
plot(x1,y1,'ob')
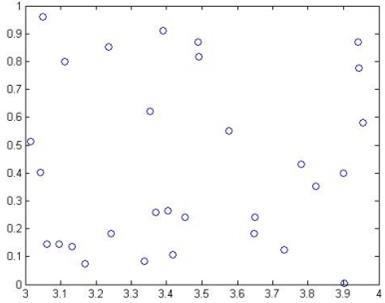
Рисунок 5.15 – Множество значений кластера 1
% Также зададим множество значений для второго кластера с центром (-3;0) (рисунок 5.16)
y2=0+rand(1,30)
x2=-3+rand(1,30)
plot(x2,y2,'or')
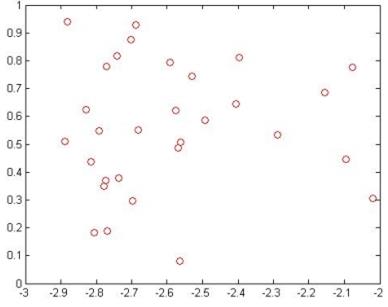
Рисунок 5.16 – Множество значений кластера 2
% Далее зададим третий и четвертый кластеры с центрами (0;3) и (0;-3)
y3=3+rand(1,30)
x3=0+rand(1,30)
x4=0+rand(1,30)
y4=-2+rand(1,30)
% Для полной наглядности посмотрим все кластеры на одном графике (рисунок 5.17)
figure (1)
hold on
plot(x3,y3,'og')
plot(x4,y4,'oy')
plot(x1,y1,'ob')
plot(x2,y2,'or')
grid on
hold off
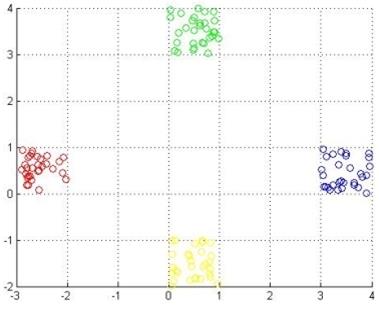
Рисунок 5.17 – Множество значений всех четырех кластеров
% Зададим цели наших четырех кластеров
T3(1:30)=10;
T4(1:30)=20;
T1(1:30)=30;
T2(1:30)=40;
% Также как в примере про feed forward сети, соединим все цели кластеров
T(1:30)=T1;
T(31:60)=T2;
T(61:90)=T3;
T(91:120)=T4;
% Перед тек подавать это на вход нейросети,
% нам необходимо соединить всю базу знаний для нейронной
% системы в одну матрицу, а именно соединим x и y и все
% это присвоим в переменную z
x(1:30)=x1;
x(31:60)=x2;
x(61:90)=x3;
x(91:120)=x4;
y(1:30)=y1;
y(31:60)=y2;
y(61:90)=y3;
y(91:120)=y4;
z(1,1:120)=x
z(2,1:120)=y
% Зададим сетку карты Кохонена гексогональную 2х2,
% так как этого нам вполне хватит
net = newsom(z,[2 2]);
% Проведем цикл обучения (рисунок 5.18)
net = train(net, z)
Заданная карта Кохонена представлена на рисунке 5.19. Распределение по кластерам всех спектров, которые мы использовали при обучении, представлено на рисунке 5.20, а распределение центров кластеров нейронной сети Кохонена – на рисунке 5.21.
% Теперь проверим получившуюся сеть на тех
% спектрах с помощью, которых мы обучали сеть
a = sim(net,z)
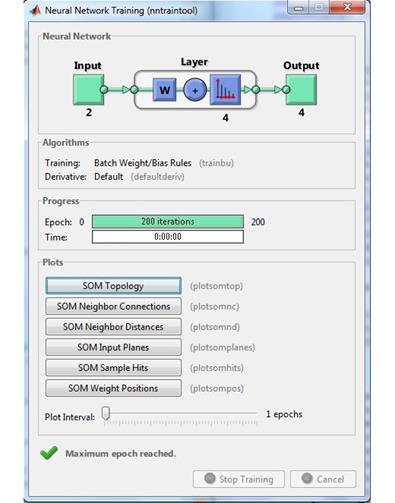
Рисунок 5.18 – Цикл обучения сети
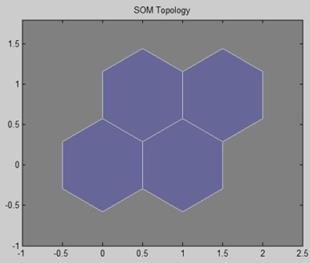
Рисунок 5.19 – Заданная карта Кохонена
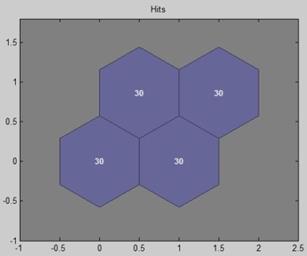
Рисунок 5.20 – Распределение по кластерам всех спектров,
используемых при обучении
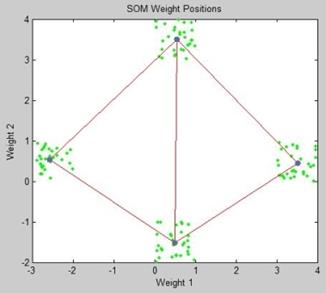
Рисунок 5.21 – Распределение центров кластеров нейронной
сети Кохонена
2.4 Задания для самостоятельной работы
1. Повторите п. 2.1 при большем объеме обучающей выборки (объем задается преподавателем). Сделайте вывод о погрешности обучения и сравните ее с изначальным результатом п. 2.1.
2. Видоизмените архитектуру сети из п. 2.2 (варианты архитектуры задаются преподавателем) и пронаблюдайте за изменением погрешности. Сделайте вывод о целесообразности выбора того или иного варианта.
3. Измените код сети Кохонена (п. 2.3) для кластеризации на шесть кластеров. Вычислите показатель ошибки обучения.
СОДЕРЖАНИЕ ОТЧЕТА
1. Цель работы.
2. Листинги написанных программ (M-файлов) в среде MATLAB для каждого задания.
3. Сводная таблица результатов, содержащая полученные в результате проведенных исследований изображения в сравнении с исходными изображениями.
4. Выводы о полученных результатах, сопоставление с теорией.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Каковы причины широкого применения нейросетей?
2. Назовите основные типы нейронных сетей, представленных в NNTool.
3. Является ли нейронная сеть линейной по своей природе?
4. Какие типы нейросетей используются в данной лабораторной работе?
5. Какие особенности имеет линейная нейронная сеть с линией задержки по входу?
6. Структурная схема нейросети в виде персептрона.
7. Что такое конкурирующая функция активации?
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Хайкин А. Нейронные сети. Полный курс // М.: Вильямс, 2006. 1104 с.
2. Дьяконов В., Круглов В. Математические пакеты расширения MatLAB. Специальный справочник // СПб: Питер, 2001. 488 с.
Учебное издание
ЦИФРОВАЯ ОБРАБОТКА
БИОМЕДИЦИНСКИХ ИЗОБРАЖЕНИЙ
Методические указания к лабораторным работам
Составитель: Мякинин Олег Олегович
Самарский национальный исследовательский университет
имени академика С.П. Королева
443086, Самара, Московское шоссе, 34
ОСНОВНЫЕ ПРИЕМЫ РАБОТЫ В СРЕДЕ MATLAB
Язык MATLAB является высокоуровневым языком программирования, включающим основанные на матрицах структуры данных, широкий спектр функций, интегрированную среду разработки, объектно-ориентированные возможности и интерфейсы к программам, написанным на других языках программирования.
Основной особенностью языка MATLAB является его широкие возможности по работе с матрицами. MATLAB предоставляет пользователю большое количество (несколько сотен) функций для анализа данных, покрывающие практически все области математики, в частности, система MATLAB предоставляет пользователю многофункциональную и эффективную среду цифровой обработки двумерных изображений: Image Processing Toolbox. Это специальный набор инструментов, расширяющий базовую функциональность среды MATLAB. Image Processing Toobox представляют собой коллекции функций, написанных на языке MATLAB для решения широкого круга задач цифровой обработки изображений.
Рабочий стол MATLAB
На рисунке В.1 приведен рабочий стол в среде MATLAB, содержащий четыре подокна: окно команд (Command Window), окно рабочего пространства (Workspace Browser), окно текущей папки (Current Directory Window), окно совершенных команд (Comand History Window). Окно команд (Command Window) – это область, где пользователь вводит команды и выражения на языке программирования среды MATLAB и где система размещает свои ответы на пользовательские команды. При каждом сеансе работы среда MATLAB формирует рабочее пространство, т.е. множество переменных, создаваемых пользователем. Окно рабочего пространства (Workspace Browser) отображает эти переменные и информацию о них – размер и тип переменной. Окно совершенных команд (Comand History Window) содержит записи всех команд, которые пользователь вводил в окне команд, включая все предыдущие сеансы работы в среде MATLAB.
Дата: 2019-02-02, просмотров: 625.
