В пакете MATLAB линейная пространственная фильтрация реализуется с помощью функции imfilter, которая имеет следующий синтаксис:
g=imfilter(f, w, filtering_mode, boundary_options, size_options)
где f – входное изображение, w – фильтрующая маска, g – результат фильтрации. Остальные параметры приведены на рисунке 1.8.

Рисунок 1.8 – Опции функции imfilter
Механизм линейной пространственной фильтрации был проиллюстрирован на рисунке 1.1. Суть процесса заключается в перемещении центра фильтрующей маски w от точки к точке изображения f. В каждой точке (x, y) отклик фильтра определяется суммой произведений коэффициентов фильтра и соответствующий пикселей окрестности, покрываемой маской. Как правило, выбирают маски нечетных размеров, в силу наличия выраженной центральной точки.
Механизм вычисления результатов фильтрации осуществляется двумя способами: корреляцией и сверткой. Корреляция состоит в прохождении маски w по изображению f , как показано на рисунке 1.1. Свертка выполняется аналогично, с тем отличием, что маску w необходимо повернуть на 1800 перед прохождением по изображению f .
Наиболее часто функция imfilter применяется в виде следующей команды:
g=imfilter(f, w, ‘replicate’)
В пакете MATLAB имеются некоторые стандартные двумерные линейные пространственные фильтры, которые можно получить с помощью функции fspecial, генерирующей маску фильтра w при выполнении следующей команды:
w = fspecial (‘ type ’, parameters )
где type обозначат тип фильтра, а parameters задают параметры выбранного фильтра.
Пространственные фильтры, получаемые данной командой, приведены на рисунке 1.9 с соответствующими параметрами каждого фильтра. Необходимо заметить, что результаты фильтрации изображений с помощью применения некоторых видов масок могут содержать отрицательные значения пикселей. При выводе таких изображений на дисплее пиксели с отрицательными значениями яркостей будут приравниваться к нулю, что приведет к сокращению динамического диапазона яркости и искажению получаемых результатов. Для преодоления указанных трудностей необходимо преобразовать исходное изображение в класс double перед фильтрацией с помощью следующей команды:
f 2= im 2 double ( f )
где f – исходное изображение класса uint 8, uint 16 или logical.
Различные классы данных приведены на рисунке 1.10. Большинство медицинских изображения представляют собой полутоновые изображения, элементы которого относятся наиболее часто к следующим классам данных: uint 8, uint 16 и double. Если элементы полутонового изображения относятся к классу uint 8 или uint 16, то они представлены целыми числами, соответственно, в интервалах [0; 255] и [0; 65535]. Если изображение принадлежит классу double, то его пиксели представляют собой вещественные числа с плавающей точкой. По общему соглашению, пиксели изображений класса double должны лежать в интервале [0; 1].

Рисунок 1.9 – Пространственные фильтры функции fspecial

Рисунок 1.10 – Классы данных
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Загрузите тестовое изображение скелета человека sceleton . jpg. Методом фильтрации с подъемом высоких частот добейтесь максимального повышение резкости исходного изображения. Для получения расфокусированного изображения используйте линейный усредняющий фильтр.
2. Примените линейную пространственную фильтрацию с помощью оператора Лапласа к исходному изображение скелета человека sceleton . jpg.
3. Сложите исходное изображение скелета человека sceleton . jpg с изображением, полученным в результате выполнения второго пункта задания.
4. Примените оператор Собела к исходному изображению скелета человека sceleton . jpg.
5. Изображение, полученное в результате выполнения четвертого пункта задания, подвергните фильтрации с помощью сглаживающего усредняющего фильтра. С помощью масок различного размера добейтесь оптимальных результатов.
6. Получите изображение путем умножения изображения, полученного после выполнения пятого пункта задания, и изображения, полученного в результате выполнения третьего пункта задания. Необходимо помнить, что речь идет о поэлементном умножении матриц изображений.
7. Получите изображения с повышенной резкостью путем сложения изображения, полученного в результате выполнения шестого пункта задания и исходного изображения изображению скелета человека sceleton . jpg.
8. Преобразуйте изображение, полученное в результате выполнения седьмого пункта задания, с помощью метода градационной коррекции по степенному закону.
9. Сравните различные методы пространственной фильтрации, использованные при выполнении всех пунктов задания. Сравните изображения, полученные в результате выполнения первого, третьего, пятого и восьмого пунктов задания. Сделайте выводы о полученных результатах.
СОДЕРЖАНИЕ ОТЧЕТА
1. Цель работы.
2. Листинги написанных программ (M-файлов) в среде MATLAB для каждого задания.
3. Сводная таблица результатов, содержащая полученные в результате проведенных исследований изображения в сравнении с исходными изображениями.
4. Выводы о полученных результатах, сопоставление с теорией.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Основной принцип метода линейной пространственной фильтрации изображений.
2. Сглаживающие линейные пространственные фильтры.
3. Пространственные фильтры повышения резкости.
4. Пространственные фильтры повышения резкости на основе второй производной.
5. Пространственные фильтры повышения резкости на основе первой производной.
6. Нерезкое маскирование и фильтрация с подъемом высоких частот.
7. Особенности применения комбинированных методов пространственной обработки биомедицинских изображений.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Гонсалес, Р. Цифровая обработка изображений [Текст] / Р. Гонсалес, Р. Вудс. – М.: Техносфера, 2006. – 1072 с.
2. Гонсалес, Р. Цифровая обработка изображений в среде Matlab [Текст] / Р. Гонсалес, Р. Вудс, С. Эддинс. – М.: Техносфера, 2006. – 616 с.
Лабораторная работа №2
«Дискретные ортогональные
преобразования»
Цель работы: изучение методов частотной фильтрации биомедицинских изображений с использованием возможностей пакета компьютерных вычислений MATLAB.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Введение в Фурье-анализ
Частотные методы улучшения изображений основаны на выполнении преобразования Фурье над функцией двух переменных – функцией дискретного изображения. Прямое дискретное Фурье-преобразование функции f(x, y), изображения размером M × N, задается равенством:
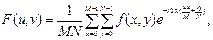
где u =0, 1, 2,…, M –1; v =0, 1, 2,…, N –1.
Обратное преобразование Фурье определяется выражением:
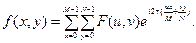
Переменные u и v называются переменными преобразования или частотными переменными, а переменные x и y называются пространственными переменными или переменными изображения. Как правило, числа M и N являются четными для упрощения компьютерной реализации, а центр Фурье образа находится в точке с координатами: u =(M /2)+1, v =(N/2)+1. Значение Фурье-преобразования в точке (u, v)=(0, 0) равно:
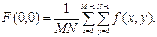
Таким образом, если f(x, y) – изображение, то значение Фурье-преобразования в начале координат равно среднему значению яркости на изображении. Поскольку началу координат отвечают нулевые частоты, то величину F(0, 0) часто называют постоянной составляющей спектра. В силу того, что функция f(x, y) вещественная, то спектр Фурье-преобразования изображения обладает свойством симметрии. Справедливы следующие соотношения между отсчетами в пространственной и частотной области:
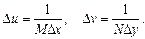
Фурье-спектр изображения состоит из пикселей, имеющих большой динамический диапазон яркости. Система воспроизведения изображений, как правило, не способна правильно отобразить столь большой диапазон значений интенсивности, что приводит к тому, что при обычном отображении спектра Фурье теряется значительное число деталей. В этой связи для улучшения зрительного восприятия полутонов, изображение спектра подвергается логарифмическому преобразованию.
На рисунке 2.1 приведено изображение, представляющее собой белый прямоугольник размерами 20×40 пикселей, наложенный на черный фон размерами 512×512 пикселей, а также представлен центрированный Фурье спектр изображения. Для того, чтобы центрировать спектр необходимо исходное изображение умножить на (–1)x+y перед вычислением Фурье-преобразования.

Рисунок 2.1 – Изображение белого прямоугольника размерами 20×40 пикселей на черном фоне размерами 512×512 пикселей (слева) и центрированный Фурье-спектр, представленный после применения логарифмического преобразования (справа)
Основы частотной фильтрации
Частотная область цифрового изображения представляет собой не что иное, как пространство, в котором принимают значения переменные (u, v) Фурье-преобразования. Как известно частота сигнала прямо связана со скоростью изменения сигнала, поэтому интуитивно понятно, что частоты в Фурье-преобразовании связаны с вариацией яркости на изображении. Наиболее медленно меняющаяся (постоянная) частотная составляющая (u=0, v=0) совпадает со средней яркостью изображения. Низкие частоты, соответствующие точкам вблизи начала координат Фурье-преобразования, определяют медленно меняющиеся компоненты изображения. По мере удаления от начала координат, более высокие частоты начинают соответствовать все более и более быстрым изменениям яркости, представляющие собой границы объектов и другие детали изображения, характеризующиеся резкими изменениями яркости, например, шум на изображении.
Процедура фильтрации изображения в частотной области состоит из следующих шагов:
1. Исходное изображение умножается на (–1)x+y, чтобы его Фурье преобразование оказалось центрированным.
2. Вычисляется прямое дискретное преобразование Фурье (ДПФ) F(u, v) исходного изображения.
3. Функция F(u, v) умножается на функцию фильтра H(u, v).
4. Вычисляется обратное ДПФ от результата шага 3.
5. Выделяется вещественная часть результата шага 4.
6. Результат шага 5 умножается на (–1)x+y.
Функция фильтра H(u, v) или передаточная характеристика фильтра подавляет некоторые частоты преобразования, оставляя другие при этом без изменения. На рисунке 2.2 представлена структурная схема, включающая основные этапы проведения фильтрации изображения в частотной области.
На стадии предварительной обработки помимо умножения изображения на (-1)x+y, могут применяться операции яркостного масштабирования, нормировка размеров исходного изображения, преобразование формата входных данных в формат с плавающей точкой и ряд других.
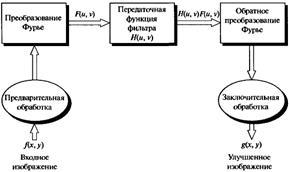
Рисунок 2.2 – Основные этапы фильтрации изображения в частотной области
Дата: 2019-02-02, просмотров: 966.