Идеальный фильтр низких частот представляют собой такой низкочастотный фильтр, который обрезает все высокочастотные составляющие Фурье-образа, находящиеся на большем расстоянии от начала координат центрированного изображения, чем некоторое заданное расстояние D ₀. Такой тип фильтра еще называется двумерным идеальным низкочастотным фильтром и имеет передаточную функцию:

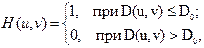
где D ₀ – заданная неотрицательная величина, точка профиля фильтра, в которой совершается переход от значений H(u, v)=1 к значениям H(u, v)=0, называемая частотой среза; D(u, v) – расстояние от точки (u , v) до начала координат – центра частотного прямоугольника.

В силу того, что Фурье-преобразование центрировано, расстояние D(u, v) определяется по формуле:

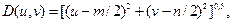
где M и N – размеры исходного изображения.

На рисунке 2.3 представлен идеальный низкочастотной фильтр в виде изображения, а также радиальный профиль фильтра:

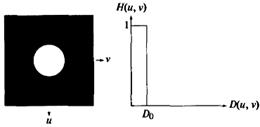
Рисунок 2.3 – Представление идеального низкочастотного фильтра в виде изображения (слева) и радиальный профиль фильтра (справа)

Идеальность фильтра подчеркивается тем, что все частоты внутри круга радиуса D ₀ проходят без изменения, в то время как частоты вне круга подавляются полностью. Низкочастотный идеальный фильтр обладает свойством симметрии относительно начала координат, поэтому для того, чтобы однозначно задать фильтр достаточно построить один радиальный профиль – функция расстояния от начала координат. Передаточная функция фильтра в координатах H(u, v) получается вращением профиля на 360⁰ вокруг начал координат.

Одним из способов выбора эталонного набора положений частот среза состоит в том, чтобы определить круги, в которых заключена заданная часть полной энергии изображения P_T. Полная энергия будет определена как сумма компонент энергетического спектра во всех точках ( u , v ); u =0, 1, 1… M –1; v =0, 1, 1… N –1.

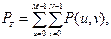
где величина P(u, v) определяется как:

P(u, v)=| F(u, v)|²,

где F(u, v) – Фурье-преобразование исходного изображения f(x, y).

Частота r(α) определятся как радиус круга с центром в центре частотного прямоугольника, содержащего α процентов энергии спектра изображения, т.е.:

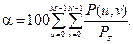
Выбор неоптимального значения частоты среза фильтра может привести к значительным искажениям обрабатываемого изображения: выбор слишком малого значения частоты среза приведет к устранению большинства деталей изображения. В то время как выбор относительно большого значения частоты среза приведет к тому, что выходное изображение будет незначительно отличаться от исходного, при этом уровень шума также не изменится.

При использовании идеального фильтра низких частот возникают нежелательные эффекты, такие как эффекты размывания и появления ложных контуров, при этом при уменьшении ширины используемого фильтра в частотной области эффекты размытия изображений усиливаются.

Возникающие нежелательные эффекты при использовании идеального фильтра низких частот получили название «звон» (или эффект Гиббса), выражающийся в появлении ложных контуров вокруг реальных контуров. Структура ложных контуров становится тоньше по мере уменьшения энергии отсекаемой высокочастотной составляющей.

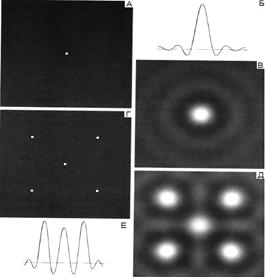
Рисунок 2.4 – А) изображение идеального фильтра низких частот; Б) профиль яркости в пространственной области; В) изображение идеального низкочастотного фильтра в пространственной области; Г) условное изображение, состоящее из пяти ярких точек в пространственной области; Д) свертка изображений В и Г; Е) профиль яркости отфильтрованного изображения Д

Природа появления ложных контуров может быть объяснена при помощи теоремы о свертке, согласно которой, существует пространственный аналог идеального фильтра низких частот. Пространственная функция такого фильтра может быть определена с помощью обратного преобразования Фурье от передаточной функции низкочастотного фильтра и представляет собой последовательность круговых концентрических колец различной яркости, приводящих главным образом к появлению ложных контуров: рисунок 2.4 иллюстрирует проявление эффекта Гиббса при использовании идеального фильтра низких частот.

Под понятием профиль яркости подразумевается зависимость изменения яркости пикселей от номера пикселей, расположенных на горизонтальной прямой, как правило, проходящей через центр изображения; отсчет пикселей по прямой начинается с крайне левого пикселя и заканчивается крайне правым пикселем.

Таким образом, приведенные результаты фильтрации с помощью идеального низкочастотного фильтра показывают, что идеальные фильтры низких частот не имеют большого практического применения.