Рассмотрим статическую систему автоматического управления углом тангажа (рис. 5), включающую контур управления угловой скоростью и контур управления углом тангажа. Передаточная функция ЛА взята в предположении постоянства скорости полета. На структурной схеме не показаны внешние возмущения 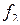 и
и 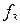 , действующие на ЛА.
, действующие на ЛА.

Рис. 5. Структурная схема системы управления углом тангажа.
Закон управления системы берем в виде:
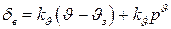 (58)
(58)
где 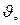 — заданное значение угла тангажа.
— заданное значение угла тангажа.
Решая уравнение (58) совместно с уравнениями (19), получим
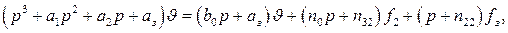 (59)
(59)
где 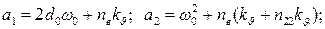
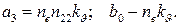
Выбор параметров системы управления следует производить из условий неискаженного воспроизведения заданного угла тангажа 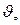 при слабом реагировании на возмущения
при слабом реагировании на возмущения 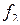 и
и 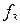 . Если передаточные числа
. Если передаточные числа 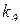 и
и 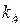 выбрать достаточно большими, то реакция системы на возмущения
выбрать достаточно большими, то реакция системы на возмущения 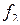 и
и 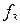 будет слабой.
будет слабой.
САУ углом тангажа посредством астатического автопилота.
Рассмотрим управление углом тангажа посредством астатического автопилота (рис. 6). Закон управления примем в виде
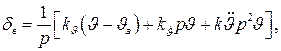 (60)
(60)
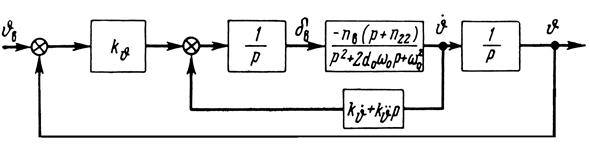
Рис. 6. Структурная схема продольного канала астатического автопилота.
Для исследования переходных процессов решим уравнение (60) совместно с уравнениями (19):
 (61)
(61)
где 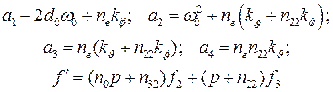
Поскольку возмущение  входит под знак оператора дифференцирования, то система не имеет статических погрешностей по отношению к углу тангажа.
входит под знак оператора дифференцирования, то система не имеет статических погрешностей по отношению к углу тангажа.
Передаточная функция по управляющему сигналу:
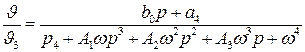 (62)
(62)
где 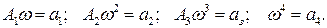
САУ углом тангажа посредством изодромного автопилота.
При изодромном автопилоте система не имеет статических погрешностей по угловым координатам, поэтому такой автопилот применяется на самолетах, требующих точной стабилизации угловых координат. Рассмотрим систему управления углом тангажа, включающую изодромный автопилот (рис. 7).
Закон управления такого автопилота, можно представить в виде
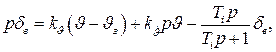 (63)
(63)
где 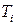 - постоянная времени изодрома.
- постоянная времени изодрома.
Если воспользоваться тем, что правая часть выражения (63) за счет функции-онирования обратной связи в каждый момент времени равна нулю, то:
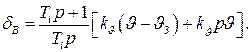 (64)
(64)
Структурная схема (рис. 7, а) соответствует выражению (64).
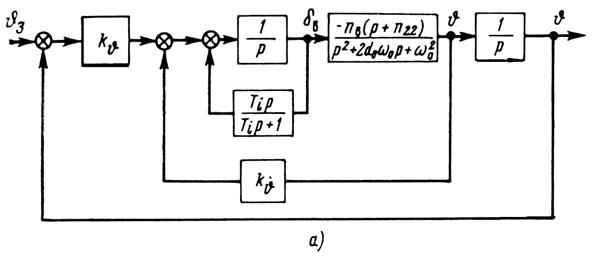
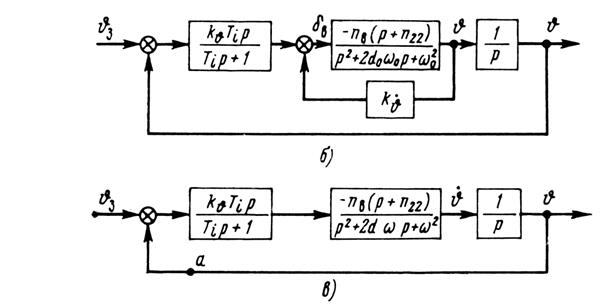
Рис. 7. Структурная схема продольного канала автопилота
Закон управления (64) отличается от закона управления статического автопилота множителем 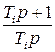 . Для высокочастотных сигналов в контуре управления угловой скоростью тангажа можно принять
. Для высокочастотных сигналов в контуре управления угловой скоростью тангажа можно принять 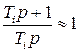 и тогда получаем структурную схему, показанную на рис. 7, б.
и тогда получаем структурную схему, показанную на рис. 7, б.
Лекция 13.
План
1. САУ углом курса. Статический автопилот.
2. САУ углом курса. Астатический автопилот.
САУ углом курса.
Рассмотрим поведение самолета по углу рыскания, управляемого автопилотом (рис. 8). Простейшим движением рыскания является колебание продольной оси самолета в горизонтальной плоскости по отношению к вектору скорости, описываемое уравнением:
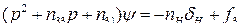 (65)
(65)
Уравнение статического автопилота возьмем в виде
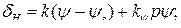 (66)
(66)
где 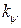 и
и 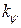 — передаточные числа;
— передаточные числа; 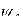 — заданный курсовой угол.
— заданный курсовой угол.
Из уравнений (65) и (66) находим
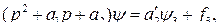 (67)
(67)
где 
Системе (67) свойственна статическая ошибка, величина которой определится из условия 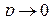 :
:
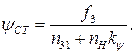 (68)
(68)
Видно, что для уменьшения статической ошибки необходимо увеличивать передаточное число по позиционному сигналу.
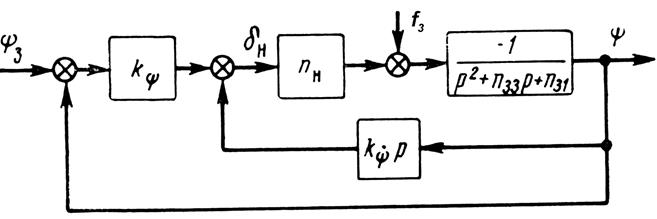
Рис.8. Структурная схема канала рысканья
Предполагая момент 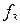 постоянным, найдем его величину для самолета с двумя двигателями, расположенными на расстоянии 5 м от продольной оси. Пусть тяга двигателя 8000 кгс, а неточность регулирования тяги составляет 10%. Возмущающий относительный момент будет (момент инерции
постоянным, найдем его величину для самолета с двумя двигателями, расположенными на расстоянии 5 м от продольной оси. Пусть тяга двигателя 8000 кгс, а неточность регулирования тяги составляет 10%. Возмущающий относительный момент будет (момент инерции 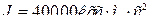 ):
):
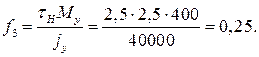
Статическая ошибка при 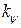 =0,545 (см. ниже)
=0,545 (см. ниже)
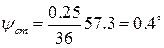
В некоторых случаях такая ошибка недопустима, поэтому вместо статического применяют астатический автопилот.
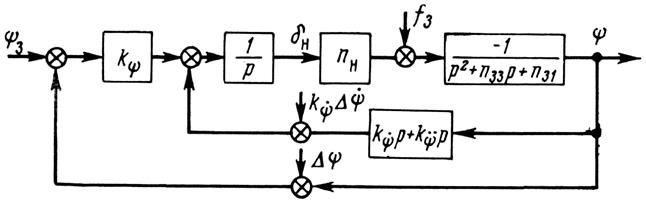
Рис. 9. Структурная схема канала рыскания астатического автопилота
Поведение самолета с астатическим автопилотом (рис. 9), закон которого возьмем в виде
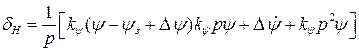 (69)
(69)
описывается уравнением
 (70)
(70)
Здесь
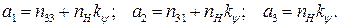
где 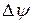 и
и 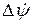 — погрешности измерения курса и угловой скорости рыскания.
— погрешности измерения курса и угловой скорости рыскания.
Из уравнения (70) видно, что поскольку возмущающий момент 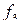 стоит под знаком дифференцирования, то статическая погрешность от этого момента будет отсутствовать. Вместе с тем видно, что погрешности в измерении курса
стоит под знаком дифференцирования, то статическая погрешность от этого момента будет отсутствовать. Вместе с тем видно, что погрешности в измерении курса 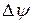 и угловой скорости рыскания
и угловой скорости рыскания 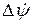 являются возмущающими факторами и целиком переходят в соответствующую погрешность стабилизации курса. Таким образом, автопилот не может стабилизировать курсовой угол (угол тангажа или крена) с большей точностью, чем точность измерения этого угла и его производных.
являются возмущающими факторами и целиком переходят в соответствующую погрешность стабилизации курса. Таким образом, автопилот не может стабилизировать курсовой угол (угол тангажа или крена) с большей точностью, чем точность измерения этого угла и его производных.
Лекция 14.
План
1. САУ углом крена.
2. Принципы построения самонастраивающихся автопилотов.
САУ углом крена.
Для управления углом крена используется специальный канал автопилота, называемый каналом крена. Законы управления канала крена обычно имеют ту же структуру, что и законы управления каналов тангажа и рыскания. Для выбора передаточных чисел канала крена необходимо исследовать динамику переходного процесса в системе, включающей самолет и канал крена.
Уравнение движения самолета по углу крена возьмем в виде
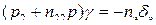 (71)
(71)
Это уравнение отличается от уравнения (32) членом 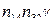 которым мы пренебрегаем ввиду его малости.
которым мы пренебрегаем ввиду его малости.
Рассмотрим поведение самолета с автоматом крена при двух законах управления:
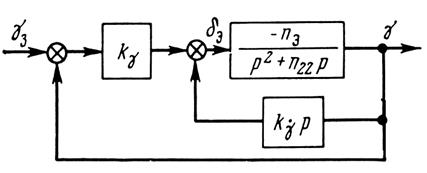
Рис. 10. Структурная схема канала крена статического автопилота
статическим (рис. 10):
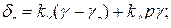 (72)
(72)
астатическим (рис. 11):
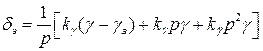 (73)
(73)
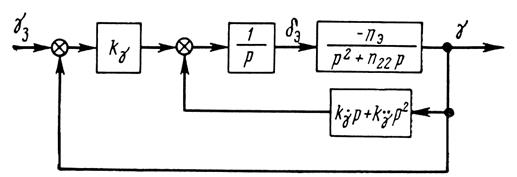
Рис. 11. Структурная схема канала крена астатического автопилота
Решая уравнения (72) и (73) совместно с уравнением (71), получим:
для статической системы
 (74)
(74)
где 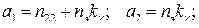
для астатической
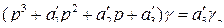 (75)
(75)
где 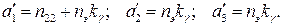
Дата: 2019-02-02, просмотров: 1237.