Для вывода линеаризованных уравнений установим зависи­мость сил и моментов от величин .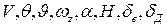

Сила тяги двигателя 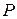 зависит от параметров двигателя и внешних условий, определяемых скоростью полета 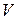, давлени­ем  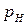и температурой  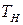атмосферы и др.  Для воздушно-реак­тивных двигателей можно написать

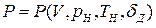                          (7)

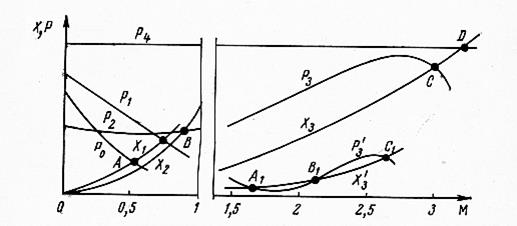
Рис. 8. Графики зависимости тяги двигателей от числа М

   На рис. 8 показана примерная зависимость силы тяги 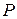 от числа М полета для поршневых ПД ( 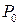), турбовинтовых, ТВД ( 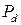), турбореактивных ТРД (  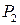- дозвуковые,  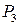— сверх­звуковые) и жидкостно-реактивных ЖРД двигателей.

  Аэродинамические силы и моменты принято представлять в виде:

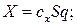
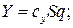
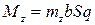                                   (8)

где 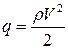    скоростной напор;  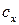и 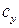 — соответственно коэффициенты лобового сопротивления и подъемной силы;  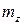— коэффициент момента тангажа;  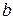— длина средней аэродинамической хорды крыла;  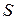— площадь крыльев.

Зависимость силы лобового сопротивления 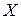 от числа М для самолетов с ПД и ТВД, ТРД и ЖРД также показана на рис. 8.

Коэффициенты 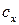 и 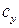 зависят от 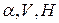, а коэффициен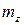т  — от .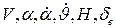

Возмущающие силы 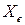 и 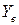 и момент 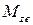, действующие на ЛА, обусловлены горизонтальными и вертикальными порывами ветра (характеризуемыми величинам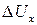и и 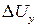), изменениями веса  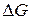(сброс грузов и др.), импульсными возмущениям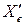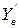и ,  и 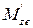, вызванными разрывами вблизи ЛА и др. Порывы ветра изменяют действующие на ЛА аэродинамиче­ские силы и моменты. Для приближенной оценки реакции ЛА на указанные возму­щения пренебрежем изменением моментов и заменим изменения аэродинамических сил вследствие порывов ветра эквивалентны­ми им ускорениями. Тогда:

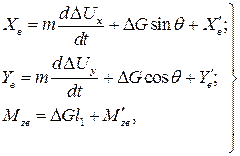                             (9)

  где 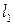 — расстояние центра масс сбрасываемого груза до цент­ра масс ЛА.

Для линеаризации уравнений (1)÷ (6) предположим, что невозмущенное движение летательного аппарата характеризуется параметрами 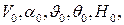удовлетворяющими тем же уравнениям. В качестве невозмущенного движения можно взять горизонтальный полет с постоянной скоростью, полет с задан­ным наклоном траектории, полет при известном программном изменении некоторых из величин, например,  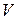или 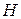 и т. д.

   Пусть в некоторый момент времени вследствие возмущений, действующих на ЛА, имеем:

,…,

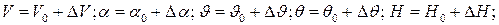где 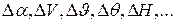 - малые приращения указанных параметров.

Из этих выражений видно, что движение ЛА можно предста­вить состоящим из невозмущенного движения и малых отклоне­ний от него.

  Разлагая силы 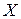, , 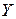 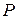и момент  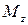в ряды Тейлора по малым приращениям и ограничиваясь линейными членами приращений, получим:

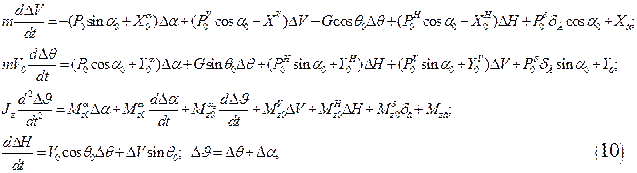
где члены с верхними индексами обозначают частные производ­ные по соответствующим переменным в окрестности невозму­щенного движения, которое обозначено нижним индексом «0».

Лекция 6.

План

1. Линеаризация уравнений продольного движения ЛА.

2. Частные случаи продольного движения ЛА.

Для частных производных, входящих в уравнения (10), можно с учетом выражений (8) написать:

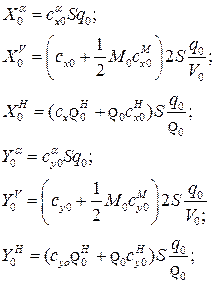
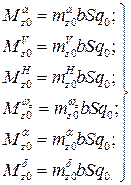                     (11)

Здесь 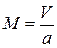 - число Маха, где  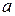- скорость звука.

При дальнейших преобразованиях воспользуемся тем, что

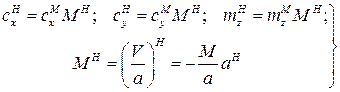                  (12)

Используемый в формулах параметр 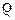 является функцией вы­соты:

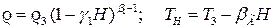                      (13)

где 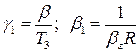;  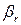— градиент температуры;  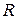— газовая постоянная; Т_н — температура на высоте 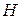;  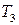и 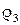 — температура и плотность атмосферы на уровне моря. После этого находим:

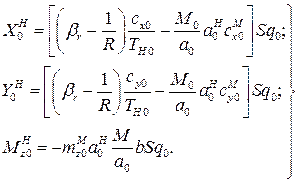               (14)

В целях сокращения записи введем относительные величины:

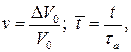                               (15)

где 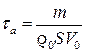- аэродинамическая постоянная времени ЛА.

Вместо приращений 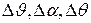 будем писать 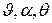, придавая последним величинам смысл тех же приращений.

Уравнения (10) с учетом введенных обозначений можно представить в виде:

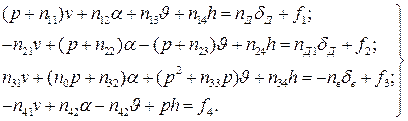       (16)

здесь

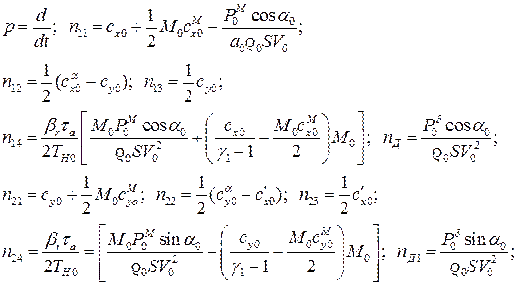
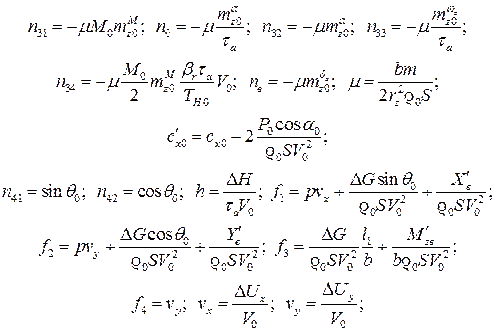
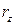 - радиус инерции самолета.

Система дифференциальных уравнений (16) является линейной математической моделью продольного движения лета­ тельного аппарата.